15 Система аксиом Вейля трехмерного евклидова пространства

1. Пусть V - трехмерное векторное пространство над полем вещест­венных чисел, а Е - непустое множество, элементы которого на­зываем точками. Мы предполагаем, что задано отображение

(:Е Х ЕV, и вектор (А, В) обозначаем через . Предполагаем также, что дано множество отображений, каждое из которых является отображением вида V Vr.

Множество Е называется трехмерным вещественным евклидовым пространством , если выполнены следующие аксиомы.⁹

1) Для каждой точки А из Е и произвольного вектора из V существует одна и только одна точка X, такая, что = .

2) Для любых точек А, В и С выполняется равенство + =.

3) Множество является множеством положительно-определен­ных билинейных форм, таких, что если , то , где λR^*₊. Другими словами, в пространстве V дана положительно-определенная билинейная форма с точностью до положительного числового множителя.

Аксиомы 1 - 2 определяют структуру трехмерного вещественного аффинного пространства Aз (с пространством переносов V).

Таким образом, базой структуры евклидова пространства Aз служит тройка множеств Е, V, R, где Е — множество точек, V — трех­мерное векторное пространство над полем R, а R— поле веществен­ных чисел.

Следовательно, при определении структуры Е ₃ мы будем исходить из того, что структура поля R вещественных чисел и структура трех­мерного векторного пространства над полем R нам хорошо известны. Тогда структура Ез определяется всего лишь тремя аксиомами Вейля 1 - 3. Эту систему обозначим через _w .

2. Докажем, что система _w непротиворечива. Для этого построим интерпретацию этой системы, используя множество R действительных чисел.

Вектором назовем любой столбец вида , где - произвольные действительные числа. Сумма векторов и умножение вектора на число определяются как сумма столбцов и умножение столбца на действительное число:

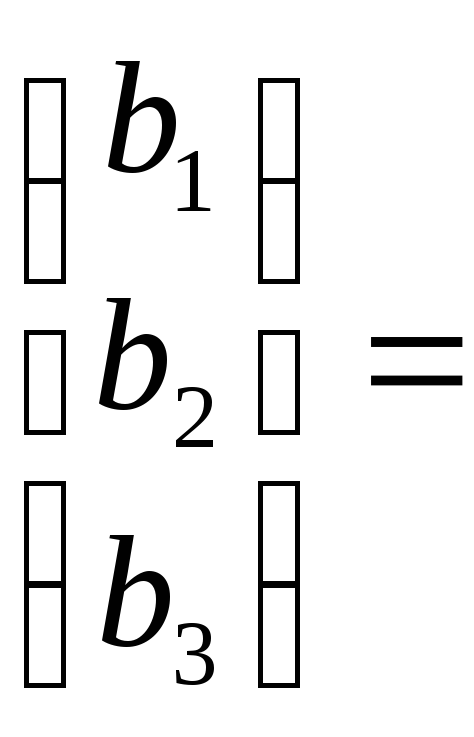
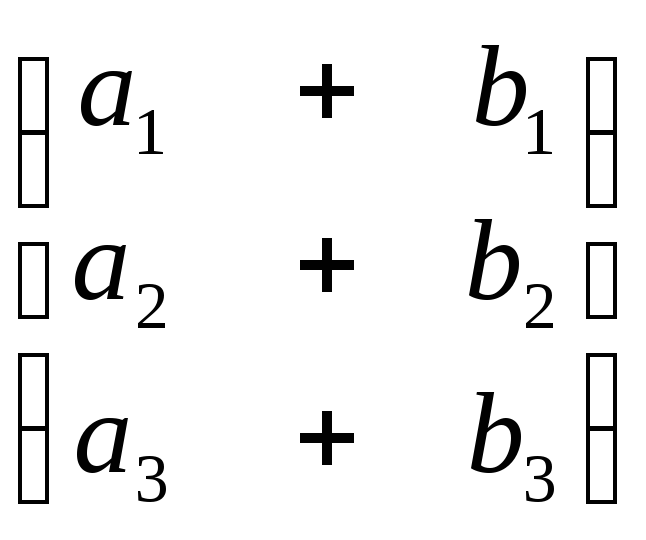+ и a.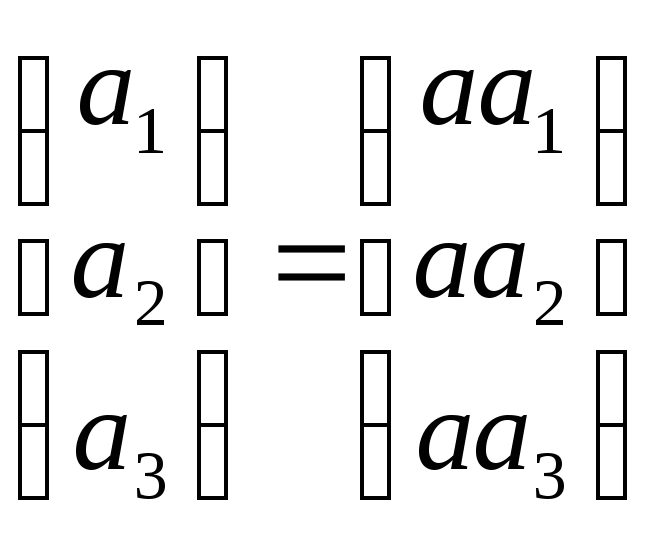

Легко видеть, что при этих соглашениях выполняются все аксиомы I₁- I₈ трехмерного векторного пространства, сформулированные в п. 1,ч. 1, § 83. При этом роль вектора играет столбец , а в качестве базиса может быть принята тройка векторов , , .

Множество положительно-определенных билинейных форм определим так. Введем в рассмотрение билинейную форму _,где

и ,

и рассмотрим множество ={λg₀}, где λ - любое действительное по­ложительное число. Очевидно, при этом выполняется аксиома 3 Вейля.

Точкой назовем любую строчку вида , где - произвольные действительные числа. Отображение :E EV определим так:

.

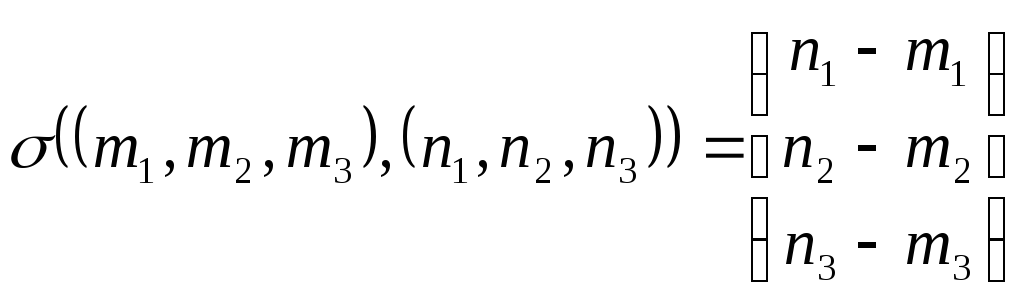Убедимся в том, что в построенной интерпретации выполняются аксиомы 1—2 Вейля.

Аксиома 1. Пусть A= (a₁, а₂, а₃) — произвольная точка, = - произволь-ный вектор. Мы должны доказать что существует одна и только одна точка , такая, что =, или в терминах нашей интерпретации , , . Ясно, что существует одна и только одна тройка чисел , удовлетворяющая этим равенствам, поэтому в построенной интерпретации выполнена аксиома 1.

Аксиома 2. Пусть А=(а₁, а₂, а₃), В= (b₁,b₂,b₃) и С =(c₁, c₂,c₃)— произвольные точки. Тогда имеем:

=, =, =.

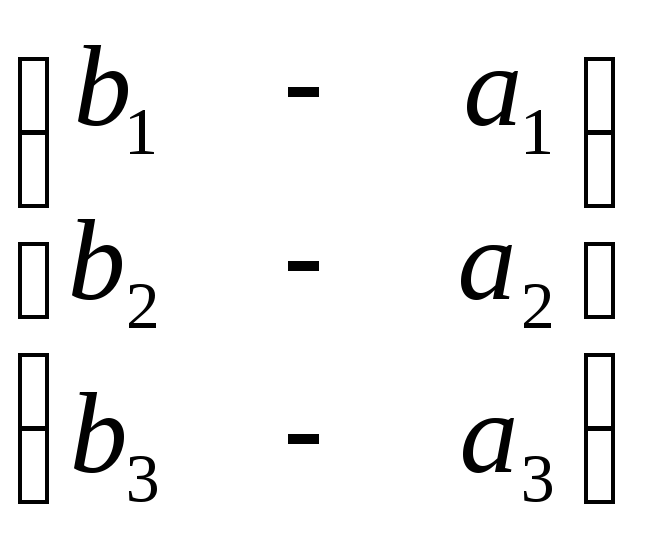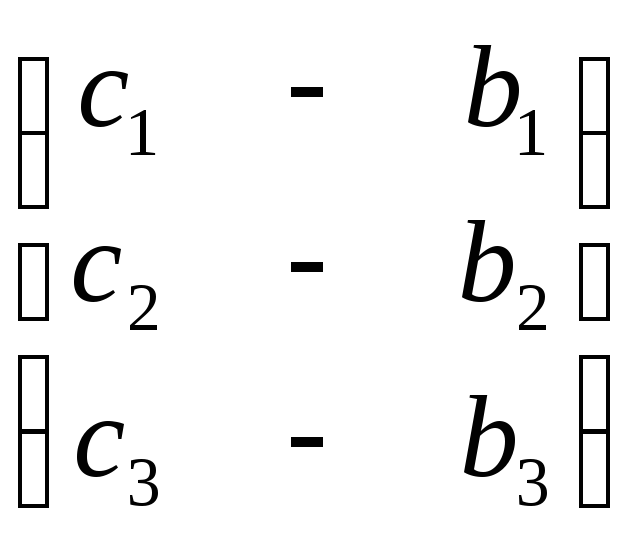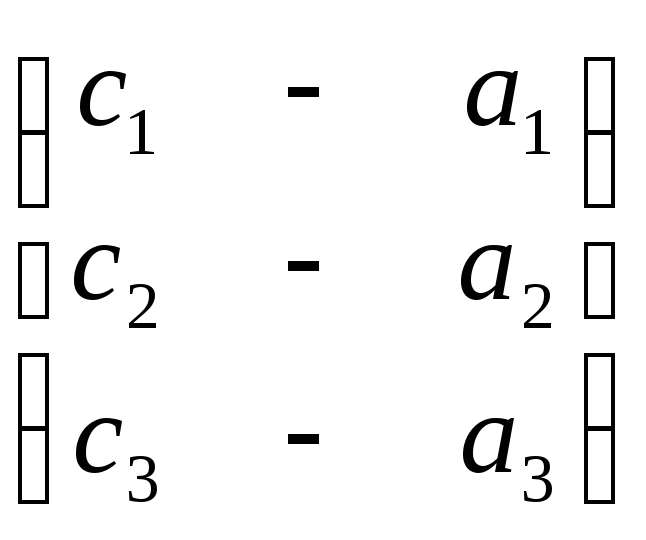Простым подсчетом убеждаемся в том, что + = . Итак, нами доказана следующая теорема.

Теорема 1. Система аксиом 1—3 Вейля непротиворечива, если непротиворечива арифметика вещественных чисел.

В ч. 1 §83 и 85 мы ввели понятия координат векторов в простран­стве V и координат точек в пространстве Ез. Тем самым мы, по существу, доказали, что любая интерпретация системы аксиом 1—3 изоморфна построенной выше интерпретации. Отсюда следует, что любые две интерпретации системы _w изоморфны, следовательно, система аксиом Вейля обладает свойством полноты (она катего­рична).

3. Покажем, что, пользуясь системой аксиом _w, можно ввести все известные нам понятия пространства Ез. Прежде всего заметим, что в пространстве Ез имеют место свойства, сформулированные в п. 1, ч. 1, §85; в частности, пространство Ез содержит бесконечное множество точек.

Напомним определения прямых и плоскостей в Ез (см. ч. 1, § 86). Пусть L_k — одномерное или двумерное подпространство трехмерного векторного пространства (т. е. k = 1 или 2). С помощью L_k введем бинарное отношение на множестве всех точек пространства Ез. Мы скажем, что точки А и В находятся в отношении , если L_k. Очевидно, — отношение эквивалентности (см. ч. 1, § 86, п. 1). Каж­дый из элементов фактор-множества Ез / при k =1 называется прямой, а при k = 2— плоскостью. Подпространство L_k называется направляющим подпространством прямой (плоскости), а векторы этого подпространства — векторами, параллельными прямой (пло­скости). Таким образом, прямая однозначно определяется заданием одной ее точки А и направляющего подпространства L₁) (или одного ненулевого вектора L₁). Аналогично плоскость однозначно опре­деляется заданием одной ее точки и направляющего подпростран­ства L₂ (или двух линейно независимых векторов ,L₂). Прямую (или плоскость), проходящую через точку А и имеющую направляю­щее подпространство L, будем обозначать так: (A, L).

Убедимся в том, что все аксиомы группы I Гильберта могут быть доказаны в теории Г(_w) как теоремы.

Выполнение аксиом I₃ и I₈ очевидно. В самом деле, пусть O — система координат пространства Ез. По первой аксиоме Вейля суще­ствуют точки А, В и С, такие, что = , = и = . Ясно, что точки О, А и В не лежат на одной прямой, а точки О, А, В и С не лежат в одной плоскости.

1°. Через любые две точки А и В проходит одна и только одна прямая (аксиомы I₁ и I₂).

Доказательство:

В самом деле, прямая d, проходящая через точку А и парал­лельная вектору , проходит также через точку В.

Если предположить, что через точки А и В проходит еще одна прямая d^/ с направляющим подпространством L^/ ₁, то АВ L^/ ₁. Отсюда следует, что направляющие подпространства прямых d и d^/ совпа­дают, и, следовательно, сами прямые d и d^/ совпадают.

Доказательство завершено.

Предлагаем читателю аналогично доказать следующее утвержде­ние.

2°. Через любые три точки А, В и С, не лежащие на одной прямой, проходит одна и только одна плоскость (аксиомы 1₄ и 1₅).

3°. Если две точки А и В прямой d лежат в плоскости , то любая точка прямой d лежит в плоскости (аксиома 1₆).

Доказательство:

Пусть (A, L₁)—прямая d, а (A, L₂)- плоскость . Так как Bd, то L₁, поэтому L1 - подпространство, натянутое на вектор . По условию В, следовательно, L₂. Таким обра­зом, L₁L₂. Если М - произвольная точка прямой d, то L₁ , следовательно, L₂, т. е. М.

4°. Если две плоскости и ^/ имеют общую точку А, то они имеют общую- прямую, которой принадлежат все общие точки плоско­стей и ^/.

Доказательство:

Пусть (A, L) — плоскость , а (A^/, L^/) — плоскость ^/. Под­пространства L и L^/ не совпадают и принадлежат векторному про­странству V, поэтому LL^/ =W, где W—одномерное векторное подпространство. Так как WL и WL^/, то все точки прямой d = (A, W) лежат в плоскостях и ^/, т. е. d— общая прямая плоскостей и ^/. Рассмотрим теперь произвольную общую точку М, плоскостей и ^/. Очевидно L и L^/, следовательно,

W. Отсюда следует, что М d.

Доказательство завершено.

Из свойства 4° следует, что в теории Г(_w) имеет место аксиома I₇ Гильберта.

4. Докажем лемму, необходимую для доказательства следующей теоремы.

Лемма. Если две прямые лежат в одной плоскости и их направ­ляющие подпространства не совпадают, то эти прямые пересекаются.

Доказательство:

Пусть и - данные прямые, лежащие в плоскости . По условию леммы векторы и не коллинеарны, поэтому образуют базис направляющего подпространства плоскости . Тогда вектор , параллельный плоскости , можно разложить по векторам и :

. (1)

По аксиоме 1 существуют точки М и М^/, такие, что = а, = -. Очевидно, М (А, ), М^/ (В, ). Подставив эти значе­ния в равенство (1), получаем = - ', или + = . По аксиоме 2 имеем = . Отсюда, учитывая аксиому 1, приходим к выводу, что точки М и М^/ совпадают, поэтому прямые (A, ) и (В, ) имеют общую точку.

Доказательство завершено.

Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек. Докажем следующий признак параллельности двух прямых.

Теорема 1. Две различные прямые параллельны тогда и толь­ко тогда, когда они имеют общее направляющее подпространство.

Доказательство:

Пусть (A,L) и (В,L) - две прямые, имеющие общее направ­ляющее подпрост-ранство L. По определению эти прямые являются разными классами эквивалентности бинарного отношения , введен­ного с помощью L. Отсюда следует, что данные прямые не имеют общих точек. Они, очевидно, лежат в плоскости, проходящей через точку А и параллельной векторам и , где — ненулевой вектор подпространства L. Следовательно, данные прямые параллельны.

Обратное утверждение непосредственно следует из доказанной леммы.

Доказательство завершено.

Теорема 2. Через данную точку А, не лежащую на данной прямой d, проходит одна и только одна прямая, параллельная пря­мой d.

Доказательство:

Пусть L — направляющее подпространство прямой d. По теореме 1 прямая (A, L), проходящая через точку А, параллельна прямой d. Докажем, что (A, L)—единственная прямая, удовлетво­ряющая этому условию. В самом деле, пусть (A, L^/) — любая прямая, проходящая через точку А и параллельная прямой d. По теореме 1 подпространства L^/ и L совпадают, поэтому прямые (A, L) и (A, L^/) совпадают.

Доказательство завершено.

Следствие. В теории Г(_w) имеет место аксиома параллель­ности (аксиома V Гильберта).

Две плоскости называются параллельными, если они не имеют общих точек. Можно доказать две теоремы о параллельных плоско­стях, аналогичные теоремам 1 и 2. Их формулировку и доказатель­ство мы предоставляем читателю.