5. Прогнозирование с применением уравнения регрессии
Если модель регрессии признана адекватной, то переходят к построению прогноза.
Прогнозируемое значение переменной у получается при подстановке в уравнение регрессии ожидаемой величины независимой переменной хпрогн:
.
Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю, поэтому рассчитывается доверительный интервал прогноза с большой надежностью:
,
где t – t-критерий Стьюдента, определяемый по таблице при уровне значимости 0,05 и числе степеней свободы k=n-2 (для парной регрессии);
– остаточная
дисперсия на одну степень свободы,
определяемая по формуле:
;
s – стандартная ошибка предсказания, определяемая по формуле:
.
Пример.
По статистическим данным, описывающим зависимость удельного веса бракованной продукции от удельного веса рабочих со специальной подготовкой на предприятиях построить уравнение парной регрессии и определить его значимость.
|
Номер предприя-тия |
Удельный вес рабочих со специальной подготовкой, % х |
Удельный вес бракованной продукции, % y |
|
1 |
15 |
18 |
|
2 |
25 |
12 |
|
3 |
35 |
10 |
|
4 |
45 |
8 |
|
5 |
55 |
6 |
|
6 |
65 |
5 |
|
7 |
70 |
3 |
Решение
1. Построим диаграмму рассеяния для определения наличия зависимости между признаками и типа этой зависимости.
Диаграмма рассеяния или корреляционное поле показывает наличие линейной обратной связи.
2. Определим линейный
коэффициент корреляции по формуле
.
Для этого построим вспомогательную
таблицу:
|
Номер предприя-тия |
Удельный вес рабочих со специальной подготовкой, % х |
Удельный вес бракован-ной продукции, % y |
(x-xср)^2 |
(y-yср)^2 |
xy |
|
1 |
15 |
18 |
857,6531 |
83,59184 |
270 |
|
2 |
25 |
12 |
371,9388 |
9,877551 |
300 |
|
3 |
35 |
10 |
86,22449 |
1,306122 |
350 |
|
4 |
45 |
8 |
0,510204 |
0,734694 |
360 |
|
5 |
55 |
6 |
114,7959 |
8,163265 |
330 |
|
6 |
65 |
5 |
429,0816 |
14,87755 |
325 |
|
7 |
70 |
3 |
661,2245 |
34,30612 |
210 |
|
Сумма |
310 |
62 |
2521,429 |
152,8571 |
2145 |
|
Среднее значение |
44,28571 |
8,857143 |
360,2041 |
21,83673 |
306,4286 |
Линейный коэффициент корреляции будет равен:
С помощью встроенной функции КОРРЕЛ Excel получаем такое же значение линейного коэффициента корреляции. Для этого в ячейку необходимо ввести =КОРРЕЛ(массив1; массив2), причем не имеет значения последовательность ввода массивов.
Таким образом, делаем вывод о сильной обратной линейной зависимости между изучаемыми признаками.
2.
Построим уравнение парной линейной
регрессии
.
Оценим параметры уравнения регрессии
а
и b
с помощью МНК. Для этого построим
вспомогательную таблицу.
|
Номер |
х |
у |
x^2 |
xy |
|
1 |
15 |
18 |
225 |
270 |
|
2 |
25 |
12 |
625 |
300 |
|
3 |
35 |
10 |
1225 |
350 |
|
4 |
45 |
8 |
2025 |
360 |
|
5 |
55 |
6 |
3025 |
330 |
|
6 |
65 |
5 |
4225 |
325 |
|
7 |
70 |
3 |
4900 |
210 |
|
Сумма |
310 |
62 |
16250 |
2145 |
Система нормальных уравнений для нахождения параметров парной линейной регрессии имеет вид:
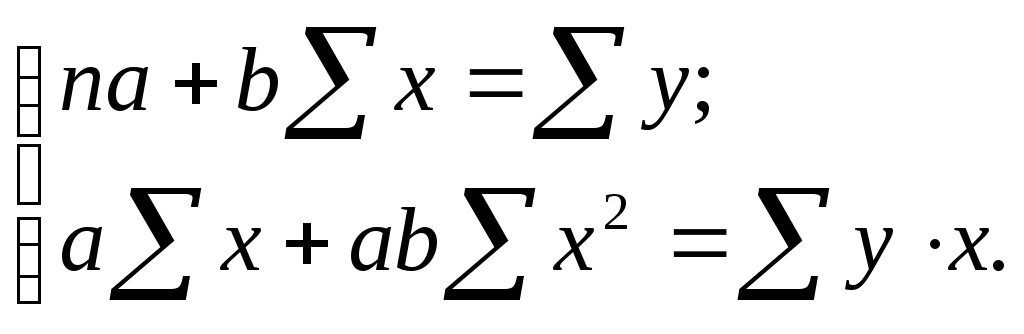
Подставим необходимые данные и получим:
Решив систему, получим
С помощью встроенной функции ЛИНЕЙН Excel получаем такие же значения параметров уравнения регрессии. Для этого необходимо выделить две ячейки в одной строке, выбрать в главном меню Вставка/Функция, далее выбрать из категории Статистические функцию ЛИНЕЙН. В образовавшемся окне заполнить аргументы функции:
Известные значения y – диапазон, содержащий данные результативного признака;
Известные значения x – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении регрессии, может принимать значение 0 или 1. Указываем 1.
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если указать 0, будут выведены только значения параметров уравнения регрессии а и b в двух выделенных ячейках.
Далее необходимо нажать ОК, одновременно удерживая клавиши Ctrl/Shift. В первой ячейке будет указано значение коэффициента при х, во второй – значение свободного члена уравнения регрессии.
Чтобы вывести всю статистику по уравнению регрессии изначально необходимо выделить диапазон из пяти строк и двух столбцов и задать логическое значение 1 в аргументе функции ЛИНЕЙН Статистика. Дополнительная регрессионная статистика будет выводится в порядке, указанном в следующей схеме:
|
Значение коэффициента а |
Значение коэффициента b |
|
Среднеквадратическое отклонение b (стандартная ошибка параметра b) |
Среднеквадратическое отклонение а (стандартная ошибка параметра а) |
|
Коэффициент детерминации R2 |
Среднеквадратическое отклонение у |
|
F-статистика (F-критерий Фишера) |
Число степеней свободы |
|
Регрессионная
сумма квадратов
|
Остаточная
сумма квадратов
|
Для разбираемого примера таблица будет выглядеть следующим образом:
|
-0,23824 |
19,40793 |
|
0,027796 |
1,339265 |
|
0,936275 |
1,395765 |
|
73,46237 |
5 |
|
143,1163 |
9,740793 |
Таким
образом, уравнение регрессии будет
иметь вид:
.
t-критерий
Стьюдента для параметра а будет равен
.
Табличное значение t-критерия
Стьюдента составляет 2,57. Поскольку
расчетное значение больше табличного
параметр а признается статистически
значимым.
t-критерий
Стьюдента для параметра а будет равен
.
Поскольку
,
параметр b
признается статистически значимым.
Т.к.
коэффициент детерминации
,
коэффициент корреляции равен
и будет иметь отрицательное значение,
поскольку связь обратная, на что указывает
отрицательный коэффициент при х
в уравнении регрессии.
Расчетное значение F-критерия Фишера равно 73,46, табличное значение F-критерия Фишера равно 6,61. Поскольку расчетное значение F-критерия больше табличного или критического, уравнение парной линейной регрессии в целом признается статистически значимым с вероятностью 95%.
t-критерий
Стьюдента для линейного коэффициента
корреляции определяется по формуле:
,
что больше табличного значения, поэтому
линейный коэффициент корреляции
признается статистически значимым.
3. Рассчитаем теоретические значения результативного признака, остатки и среднюю ошибку аппроксимации:
|
Номер |
х |
у |
|
|
|
|
1 |
15 |
18 |
15,83428 |
2,16572238 |
0,120318 |
|
2 |
25 |
12 |
13,45184 |
-1,45184136 |
0,120987 |
|
3 |
35 |
10 |
11,06941 |
-1,069405099 |
0,106941 |
|
4 |
45 |
8 |
8,686969 |
-0,686968839 |
0,085871 |
|
5 |
55 |
6 |
6,304533 |
-0,304532578 |
0,050755 |
|
6 |
65 |
5 |
3,922096 |
1,077903683 |
0,215581 |
|
7 |
70 |
3 |
2,730878 |
0,269121813 |
0,089707 |
|
Сумма |
310 |
62 |
62 |
0 |
0,79016 |
Средняя
ошибка аппроксимации равна:
.
Таким образом, при прогнозировании по
данной модели в среднем ошибка составит
11%, в то время как предельные допустимые
значения этого показателя составляют
8-10%. Большая средняя ошибка аппроксимации
получилась за счет малого числа
наблюдений.