20) Канонические формы квазилинейных дифф ур-й с частными производными второго порядка

21) Задача о свободных колебаниях конечной струны. Метод Фурье,

Пусть имеется натянутая однородная струна конечной длинны l постоянного поперечного сечения закрепленная на концах. Под струной понимается тонкая нить которая может изгибаться свободно, т.е. не оказывает сопротивления изменению ее формы не связанному с изменением ее длинны.

Сила натяжения действует на струну так что можно пренебречь силой тяжести. Поэтому можно считать что в положении равновесия струна направлена по сои Ох и занимает отрезок [0,l]. Если струна отклонилась то она будет содержать колебания положения равновесия. Будем рассматривать только поперечные колебания, т.е колебания происходящие в хОу

U(x,t) - смещение точки струны в момент времени t от положения равновесия, тогда при фиксированном значении t график ф-и U(x,t) дает форму струны в этот момент времени.

Метод Фурье

Решение задачи о струне задается формулой U(x,t)=Σ(akcos(πka/l)+bksin(πka/l)*t)sinπkx/l где коэф ak и bk определяются по формуле

ak=2/lSf(x)sin(πkx/l)dx

bk=2/πkaSF(x)sin(πkx/l)dx

22)Приближенные методы решений уравнения

f(x)=0 (1)

Приближенное нахождение корней – нахождение таких значений аргумента х=с при которых имеет место след-е соотношение

f(c) приблизительно равно 0, при этом под близостью приближения значения с и корня ур-я (1) понимается как правило вып-е след неравенства

[x-c]<ε

ε – точность

Локализация корней

1)метод дихотомии

Пусть дано ур-е (1) где f(x) непрерывна на отрезке [a,b] f(a)f(b)<0 и на этом отрезке сущ-т единственный корень ур-я (1)

Выберем в качестве (a,b) произвольную точку с

При этом возникают след-е ситуации: 1) f(c)=0 2)f(a)f(c)<0 [a,c] 3)f(b)f(c)<0 [c,b]

Таким образом с помощью одной пробной точки можно либо найти корень ур либо умножить отрезок сущ-я корня

Частные случаи метода дихотомии

1)метод половинного деления - в качестве точки с выбираем середину отрезка [a,b]

С=a+b/2

1)Зададим ф-ю f(x),концы отрезка [a,b] и плотность Е. 2)Вычислим c=a+b/2

3)Если f(c)=0 то перейти в пункт 8 4)если f(a)f(c)<0 то b:=c 5)f(a)f(c)>0 a:=c

6)вычислим a+b/2 7)повторяем пункты 3-6 до тех пор пока длинна этого отрезка не станет меньше чем Е (b-a>=E) 8)корень ур-я будет число с

2)метод хорд

Точка с будет отыскиваться как абсцисса точки пересечения с осью Ох прямой соед-й точки A(a,f(a)) и B(b,f(b))

Метод Ньютона(метод касательных)

23)Полиномиальная интерполяция. Многочлен Лагранжа

В основе большинства численных методов лежит замена одной ф-и f(x) и другой близкой к ней ф-и фи(х) обладающей «хорошими» свойствами, которые позволяют легко производить над ней те или иные аналитические или вычислительные операции.

Будем называть такую замену аппроксимацией ф-и f(x) и ф-и фи(х)

anx0n+an-1x0^n-1+…+a1x0+a0=y0

anx1^n+an-1x1^n-1+…+a1x1+a1=y1 (*)

…

ax^nn+an-1x^n-1n+…+a1xn+a0=yn

(**)

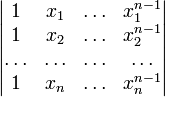Определитель матрицы (**) наз-я определителем Вандермонда

Изветно что опр Вандермонда отличен от 0, а значит система (*) имеет и при том единственное решение,след-о можно построить ед-й многочлен для ф-и f(x), этот многочлен и наз-я интерполяционным многочленом Лагранжа