
-
Электронный усилитель 1
Усилитель выбран из линейки промышленных усилителей мощности фирмы Cridom и описывается дифференциальным уравнением 1 порядка:
![]() ,
,
U2 – выходное напряжение усилителя (В),
U1 – входное напряжение усилителя (В),
к – коэффициент усиления усилителя по напряжению.
Тогда передаточная функция усилителя мощности имеет вид апериодического звена 1 порядка:
![]()
Коэффициент усиления усилителя выбираем из условия согласования выходного сигнала регулятора 0-5В с напряжением последующего усилителя равным 24В.
![]()
В паспорте к усилительному элементу типа В D4825 указывается время переходного процесса tпер = 0,004 сек. Для звена 1 порядка время переходного процесса связано с постоянной времени следующей зависимостью:
![]()
По этой формуле постоянная времени усилительного элемента равна:
![]()
Тогда окончательно передаточная функция ключевого элемента имеет вид:
![]()
-
Электронный усилитель 2
Данный элемент усиливает сигнал 24В в сигнал 220В для управления исполнительным механизмом.
Передаточная функция этого элемента будет:
![]()
![]()
3.4 Исполнительный механизм
Исполнительным механизмом является механизм электрический однооборотный, который включает в себя три звена. Определим передаточные функции этих звеньев.
3.4.1 Двигатель. По паспортным данным используется двигатель типа ДАУ-25.
Мощность двигателя (Nдв) – 25Вт,
Напряжение питания (Uп) – 220В,
Число полюсов (n) – 12,
Момент нагрузки на валу (Мн) – 40Нм.
Передаточная функция двигателя рассчитывается по формуле:
![]()
![]()
![]()
![]()
![]()
3.4.2 Редуктор. Передаточной функцией редуктора является обратная величина его передаточному отношению (i).
![]()
По паспортным данным передаточное число редуктора = 416,7
![]()
3.4.3 Клапан. Передаточная функция клапана рассчитывается по формуле:
![]()
Коэффициент
передачи
![]() найдем
по статической характеристике:
найдем
по статической характеристике:
![]()
![]()
Передаточная функция исполнительного механизма будет выглядеть следующим образом:
![]()
![]()
3.5 Объект регулирования
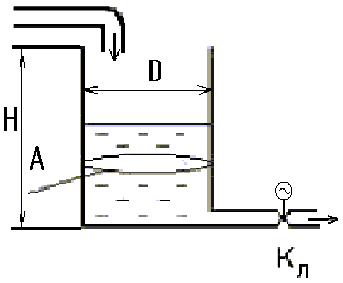
Рисунок 8 - Объект регулирования (емкость с жидкостью)
Объект регулирования является устойчивым звеном первого порядка, и его передаточную функцию найдем по формуле:
![]()
Коэффициент передачи будет равен:
![]()
Постоянная времени объекта регулирования найдем по формуле:
![]()
![]() - время разгона
ОР,
- время разгона
ОР,
![]() - площадь
горизонтального сечения ОР,
- площадь
горизонтального сечения ОР,
![]() -
значения соответствующих величин при
равновесном состоянии ОР,
-
значения соответствующих величин при
равновесном состоянии ОР,
![]()
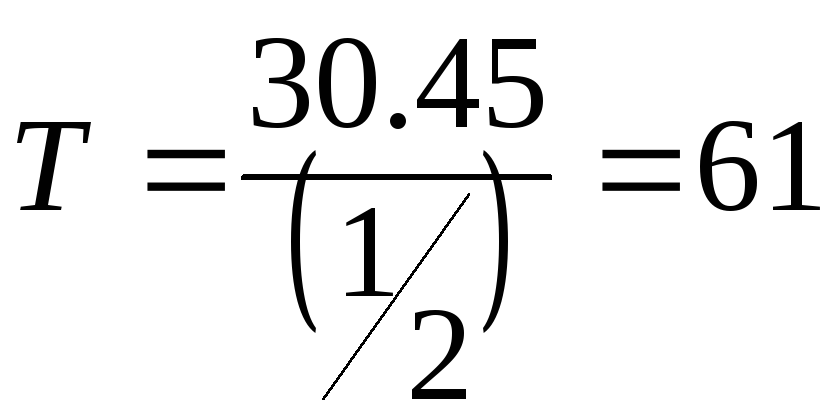
Получим передаточную функцию:
![]()
3.6 Микроконтроллер
Рассмотрим микроконтроллер, как импульсный элемент системы и рассчитаем его дискретность.
Входы и выходы микроконтроллера аналоговые с дискретностью 8 бит – 256, при напряжении 0-5 вольт на входах и выходах, микроконтроллер выдает разрешение 0,02 В, что позволяет судить о его практической линейности по входам и выходам.
Частота кварца микроконтроллера равна 12 МГц. Один такт программы выполняется за 1/12 частоты микроконтроллера, соответственно за 1 минуту производится 6107 тактов программы.
Предположим, что для принятия решения микроконтроллера необходимо 103 тактов программы, тогда дискретность микроконтроллера равна 6104 тактов в минуту, а период дискретности Т=1,610-5 минуты, что сводит к нулю дискретность микроконтроллера по времени, так как наибольшая постоянная времени равна 1мин.
Делаем вывод, что микроконтроллер не вносит помех в рассматриваемую систему, и его передаточную функцию принимаем за единицу.
![]()
3.7 Структурная схема системы
Функциональная схема автоматического регулирования уровня в емкости, включающей передаточные функции элементов, представлена на рисунке 9. Все передаточные функции элементов согласованы по типу сигналов, диапазонам их изменения и мощности.

Рисунок 9 - Структурная схема системы
4 Анализ системы
4.1 Расчет системы на устойчивость
Все расчеты системы произведены в программе MathCad 2000.
Передаточная характеристика разомкнутой системы равна:
![]()
Т.к. постоянная времени Т1=0,031 намного меньше Т2=61, то мы ей пренебрегаем и получаем передаточную функцию:
![]()
Получим передаточную характеристику замкнутой системы:
![]()
Подставим вместо р j, получим:
![]()
Найдем реальную и мнимую части:
![]()
![]()
Построим годограф Найквиста:
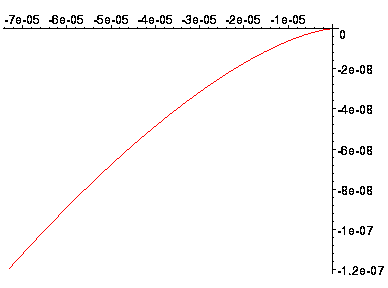
Рисунок 10 - Годограф Найквиста
Годограф Найквиста не захватывает точку (-1,j0), соответственно система устойчива.
4.2 Построение ЛАЧХ и ЛФЧХ системы
Для построения ЛАЧХ разомкнутой системы применим формулу:
![]()
Построим ЛАЧХ и ЛФЧХ системы:
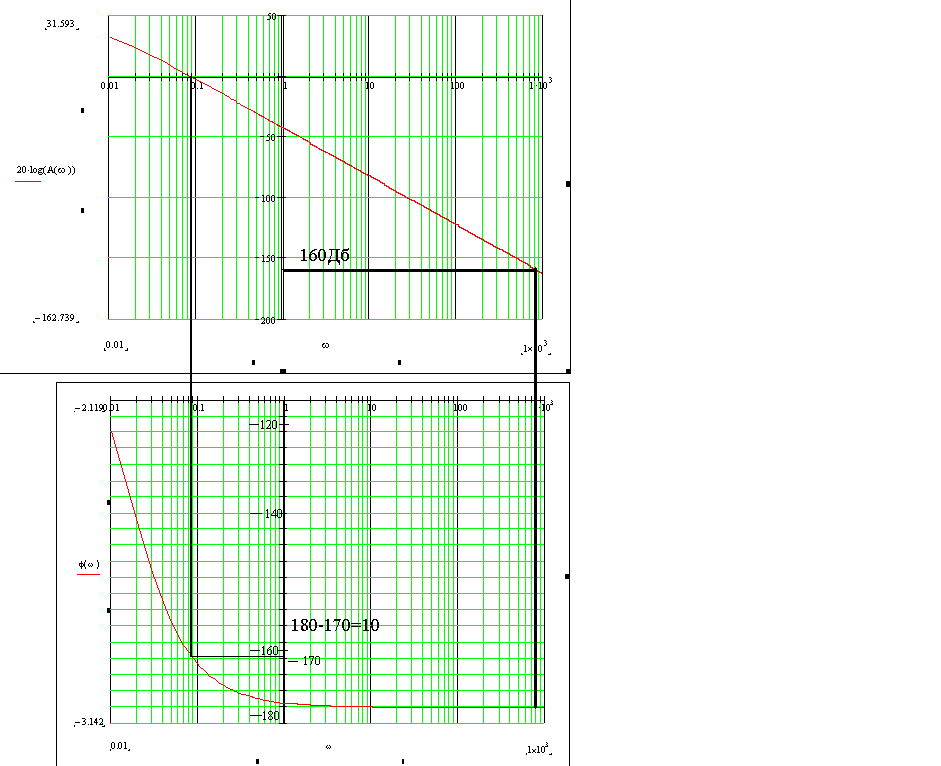
Рисунок 11- ЛАЧХ и ЛФЧХ
По полученным характеристикам определяем запас по амплитуде и запас по фазе. Запас устойчивости по амплитуде находят по ординате ЛАЧХ в точке пересечения ЛФЧХ с прямой (-180). Запас устойчивости по фазе определяется превышением над прямой (-180) на частоте среза с.
Запас по фазе получили 10. Такой запас по фазе нас не удовлетворяет, т.к. он должен превышать (30-40) .
Запас по амплитуде получили более 160Дб.
4.3 Построение переходного процесса не скорректированной системы
По передаточной функции замкнутой системы построим переходный процесс не скорректированной системы:
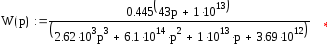
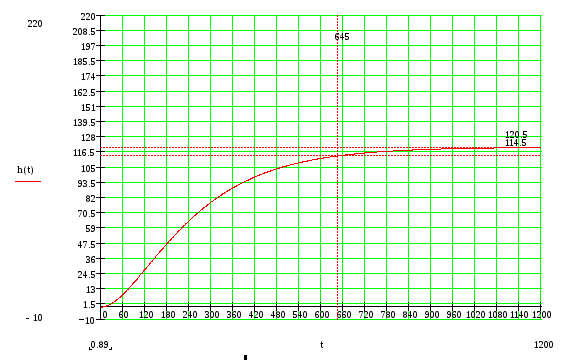
Рисунок 12 - переходный процесс не скорректированной системы
По переходному процессу видим, что время регулирования tр=645с, перерегулирование =0%, что не удовлетворяет нашему техническому заданию.
5 Синтез системы
5.1 Построение желаемой ЛАЧХ
Зададимся, по техническому заданию, временем регулирования tр=60с, перерегулированием =18%, и по номограмме Солодовникова найдем частоту среза с.
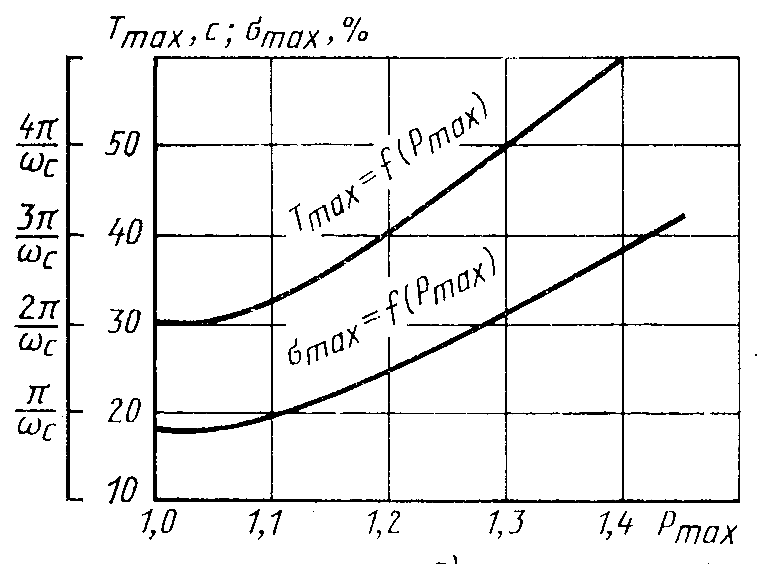 Рисунок 13 - номограмма
Солодовникова
Рисунок 13 - номограмма
Солодовникова
Для =18%, частоту среза с найдем по формуле:
![]() ,
,
![]() ,
при tр=60с,
частота среза с
будет ровна:
,
при tр=60с,
частота среза с
будет ровна:
![]()
Построим желаемую ЛАЧХ и ЛАЧХ корректирующего устройства.
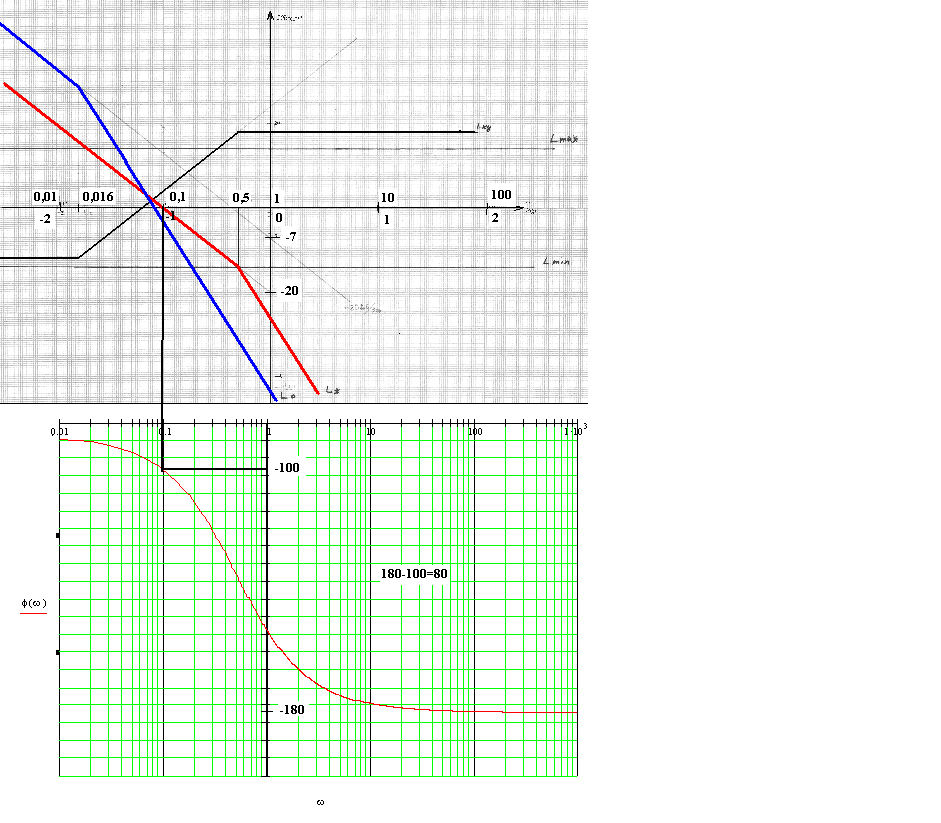
Рисунок 13 - ЛАЧХ, ЖЛАЧХ и ЛАЧХ корректирующего устройства
По полученным характеристикам определяем запас по амплитуде и запас по фазе.
Запас по фазе получили 80. Такой запас по фазе нас удовлетворяет, т.к. он должен превышать (30-40) .
Запас по амплитуде остался прежним.
5.2 Расчет корректирующего устройства
Подберем аналоговое корректирующее устройство из ряда последовательных корректирующих устройств. Передаточная функция нашего корректирующего устройства будет выглядеть следующем образом:
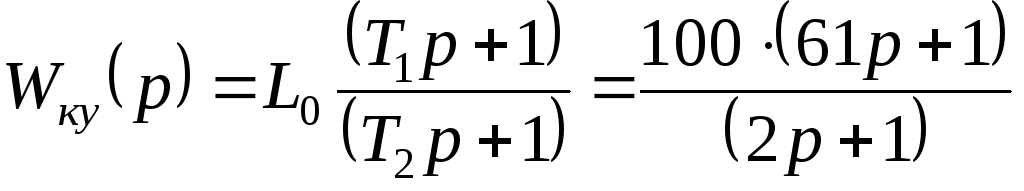 ,
,
![]() ,
,
![]()
R1=100
Ом, С1=61/100=0,61
Ф,
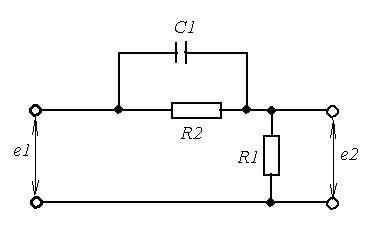
![]() R2=2950
Ом
R2=2950
Ом
Рисунок 14 - Схема корректирующего устройства
Тогда передаточная характеристика скорректированной разомкнутой системы будет:
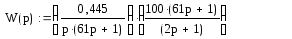
![]()
Построим годограф Найквиста:
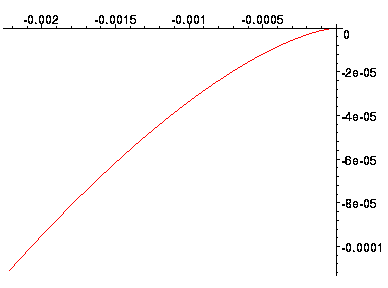
Рисунок 15 - Годограф Найквиста
Годограф Найквиста полученной системы не захватывает точку
(-1,j0), соответственно разомкнутая система устойчива.
5.3 Построение переходного процесса скорректированной системы
По передаточной функции замкнутой системы построим переходный процесс скорректированной системы:

По переходному процессу видим, что время регулирования tр=12,25с.
Перерегулирование:
![]() ,
,
что вполне удовлетворяет нашему техническому заданию.
