2.5 Передаточная функция объекта управления

Объектом управления является нагнетающий трубопровод. Так как длина нагнетающего трубопровода мала, то емкостью трубопровода можно пренебречь. Тогда передаточная функция объекта управления примет вид:

(19)

где T_L – постоянная времени;

k – коэффициент передачи.

(20)

Для трубопровода круглого сечения

(21)

где  - кинематический коэффициент вязкости рабочей жидкости.

Рабочая жидкость – вода ГОСТ20799-88: =3210^-5 м²/с при 40С; =890 кг/м³ при 20С.

(22)

(23)

Передаточная функция объекта управления:

(24)

3. РАСЧЕТ УСТОЙЧИВОСТИ СИСТЕМЫ

3.1 Исследование линейной части системы

Рисунок 4 – Структурная схема системы управления давлением

Передаточная функция замкнутой системы:

(25)

(26)

Передаточная функция разомкнутой системы:

(27)

(28)

Определим устойчивость системы регулирования по критерию Гурвица. Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны. Определитель Гурвица составим по коэффициентам характеристического уравнения.

(29)

(30)

(31)

(32)

(33)

(34)

Все миноры определителя Гурвица положительны, следовательно, система устойчива.

Произведем обратное преобразование Лапласа и получим переходную функцию системы, построим график переходного процесса:

(35)

Рисунок 5 – График переходного процесса

Определим графически прямые оценки качества системы.

Время переходного процесса t_П – это время регулирования системы. Определяется как интервал от момента приложения какого-либо воздействия на систему до времени вхождения системы 5 % трубу. Определяет быстродействие системы.

t_П = 0,27 с.

Перерегулирование δ (максимальная динамическая ошибка):

 = 0 %

Колебательность n – число колебаний системы от момента воздействия на нее до перехода в установившееся состояние: n = 0

Заменим в передаточной функции замкнутой системы оператор р на jw

(36)

(37)

(38)

Рисунок 6 – АЧХ системы

Определим косвенные оценки качества системы.

Показатель колебательности:

(39)

Резонансная частота ω_p – частота, при которой АЧХ достигает максимальное значение: рад/с

С учетом прямых и косвенных оценок качества можно сделать вывод, что качество управления достаточно высокое.

3.2 Проведение z-преобразования

Проведение z-преобразования осуществляется с помощью программы Matlab. Учитывая, что время дискретизации системы T₀=0,05с, получим передаточную функцию для дискретной системы:

(40)

Текст рабочей программы для получения передаточной функции дискретной системы:

>> Wpzam=Tf([1.71*10^-5 3.98*10^-4],[6.55*10^-8 2.73*10^-5 3.63*10^-3 0.114 1])

Transfer function:

1.71e-005 s + 0.000398

---------------------------------------------------------

6.55e-008 s^4 + 2.73e-005 s^3 + 0.00363 s^2 + 0.114 s + 1

>> Wzzam=c2d(Wpzam,0.05)

Transfer function:

0.0001917 z^3 - 2.973e-005 z^2 - 9.411e-006 z - 5.648e-010

----------------------------------------------------------

z^4 - 0.7525 z^3 + 0.1357 z^2 + 2.152e-005 z + 8.901e-010

Sampling time: 0.05

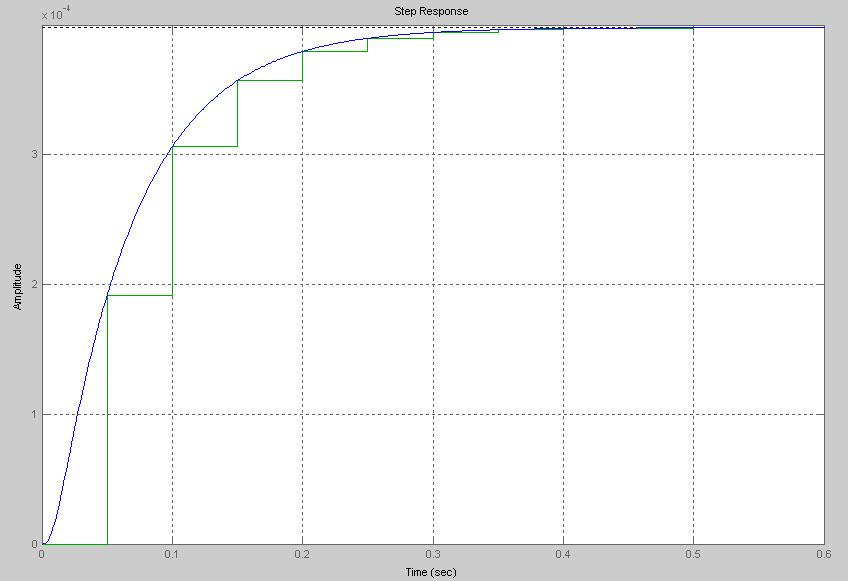>> Step (Wpzam, Wzzam)

Рисунок 7 – График непрерывного и дискретного переходных процессов

По графику видно, что дискретная система переходит в установившееся состояние за 0,35 с, что вполне удовлетворяет требованиям по быстродействию.

3.3 Определение устойчивости дискретной системы по расположению кор-

ней характеристического уравнения

Передаточная функция замкнутой дискретной системы имеет вид:

(41)

Характеристическое уравнение имеет вид:

₍₄₂₎

_{Для устойчивости системы необходимо чтобы корни характеристического уравнения (42) лежали внутри окружности с единичным радиусом с центром в точке (0;j0).}

_{Получим корни характеристического уравнения:}

Условие выполнено, система устойчива.

4 ПОСТРОЕНИЕ ЛАЧХ, ЛФЧХ СИСТЕМЫ И ИХ АНАЛИЗ

4.1 Z-преобразование разомкнутой системы

Передаточная функция разомкнутой системы:

(43)

Переход к дискретной передаточной функции осуществляется с помощью программы Matlab, по уравнению (44), учитывая время дискретизации системы Т=0,05 с.

(44)

Текст рабочей программы:

>> Wpraz=Tf([4.98*10^-8],[6.59*10^-8 2.73*10^-5 3.63*10^-3 0.113 1])

Transfer function:

4.98e-008

---------------------------------------------------------

6.59e-008 s^4 + 2.73e-005 s^3 + 0.00363 s^2 + 0.113 s + 1

>> Wzraz=c2d(Wpraz,0.05)

Transfer function:

9.379e-009 z^3 + 9.593e-009 z^2 + 2.116e-010 z + 1.435e-014

-----------------------------------------------------------

z^4 - 0.7544 z^3 + 0.1396 z^2 + 2.251e-005 z + 1.01e-009

Sampling time: 0.05

>>

Передаточная функция разомкнутой дискретной системы:

(45)

4.2 Переход к псевдочастоте, построение ЛАЧХ, ЛФЧХ

Для построения ЛАЧХ необходимо перейти к псевдочастоте, производя ряд

замен.

Производим замену в выражении (37) (46)

(47)

Произведем замену в выражении (47) на (48)

где T₀=0,05c – период дискретизации системы.

Данная частота дискретизации выбрана исходя из требований точности регулирования.

(49)

(50)

(51)

Построение ЛАЧХ:

(52)

Рисунок 8 – ЛАЧХ дискретной системы, построенная в программе

МАTHCAD

Построение ЛФЧХ:

(53)

Рисунок 9 – ЛФЧХ дискретной системы, построенная в программе

МАTHCAD

Как видно запасы устойчивости системы составляют:

-запас устойчивости по амплитуде Gm=159 дБ;

-запас устойчивости по фазе бесконечен.

Это значит, что система находится в устойчивом состоянии и удовлетворяет требованиям по надежности и быстродействию. Можно придти к выводу, что у данной системы нет необходимости в коррекции.