9 Уитс.421243.010 пз Со — емкость одной пластины, ф.

В данном случае примем n=1, и пренебрежем значением емкости измерительной цепи.

Емкость одной пластины датчика толщиной d и площадью s можно определить как емкость плоскопараллельного конденсатора:

, (6)

где

ε₀ - абсолютная диэлектрическая проницаемость вакуума,

ε₀ = 8.85*10^-12 Ф/м;

ε - диэлектрическая проницаемость пьезоматериала;

s – площадь пластины, м²;

d – расстояние между пластинами,м.

Емкость пьезоэлемента С на практике бывает невелика и выражается в пикофарадах (1 пФ = 10^-12 Ф).

Выходной сигнал пьезодатчика

F= U/S_a, (7) где F-создаваемая сила, но

F=m*a, (8)

где

m – инерционная масса активатора, кг;

a – виброускорение, создаваемое активатором, причем

а = N*g, (9)

g = 9.8 м/с² – ускорение свободного падения;

N – коэффициент пропорциональности.

10

УИТС.421243.010 ПЗ

Решая совместно уравнения (6) – (9) получим:

, (10)

То есть получили зависимость геометрических параметров пьезоактиватора от напряжения.

Выбираем передаточная функция пьезоактиватора. Он реализует функцию инерционного звена.

Передаточная функция

(11)

2.6 Датчик расхода

Датчик расхода в данной системе подбирается по передаточной функции. Это очень чувствительный элемент. Рассчитаем необходимую чувствительность датчика.

В среднем, одной заправки 10 мл чернил хватает на 500 листов текстовой информации а на один лист А4 приходится примерно 2500 печатных знаков 14 шрифтом Times New Roman, то можно подсчитать расход чернил на 1 символ.

Q₁=мл (12)

Таким образом датчик должен обеспечивать такую высокую точность измерений.

Датчик реализует функцию пропорционального звена.

Выберем для нашей системы передаточную функцию вида

Wdr=0.07 (13)

11

УИТС.421243.010 ПЗ

3 ДЕЛЕНИЕ ЛСУ НА ИЗМЕНЯЕМУЮ И НЕИЗМЕНЯЕМУЮ ЧАСТИ.

ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ

К неизменяемой части относят все элементы регулятора с передаточной функцией отличной от единицы. Следовательно, к ним можно отнести все элементы кроме микропроцессора.

Определим передаточную функцию системы, передаточная функция главной цепи будет:

. (14)

(15)

Передаточная функция разомкнутой системы будет:

. (16)

(17)

Передаточная функция замкнутой системы:

. (18)

12

УИТС.421243.010 ПЗ

По выражению (16) построим АФЧХ разомкнутой системы, изображенную на рисунке 2:

Рисунок 2 – АФЧХ разомкнутой системы

Согласно критерию Найквиста, замкнутая автоматическая система регулирования будет устойчивой, если АФХ разомкнутой системы не охватывает точку с координатами -1,j0 ,таким образом, имеем устойчивую систему с неограниченно большими запасами по амплитуде и фазе.

13

УИТС.421243.010 ПЗ

Переходный процесс в замкнутой системе изображен на рисунке 3. Из него видно что переходный процесс длится более 16 секунд лишь потом становится устойчивым. Такой отпечаток накладывает инерционное звено.

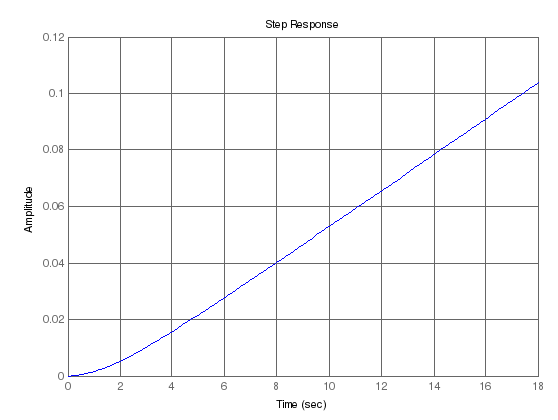
Рисунок 3 – переходный процесс замкнутой системы

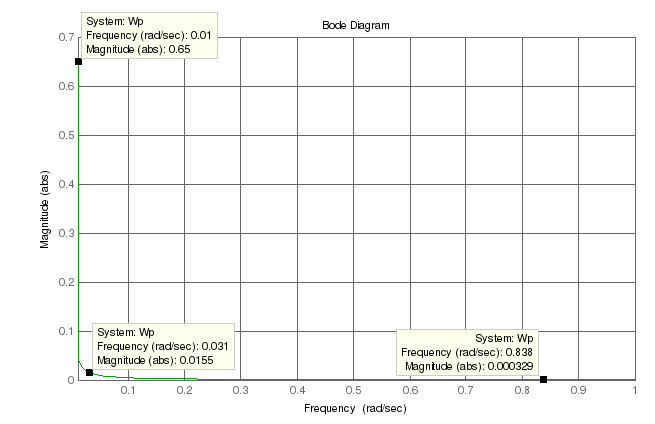АЧХ системы выглядит следующим образом:

Рисунок 4 – переходный процесс разомкнутой системы

Запасы устойчивости определим по АЧХ системы:

запас по амплитуде 119 дБ

запас по фазе 93,7 градусов

14

УИТС.421243.010 ПЗ

4 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК И ИХ

АНАЛИЗ

4.1 Построение ЛАЧX

Разомкнутая система образована апериодическим, пропорциональным и колебательным звеньями:

(19)

ω₁=1/T₁= 0,5882рад/c,

ω₁=1/T₁=3.02*10³ рад/c.

По выражению (16) построим ЛАЧХ и ЛФЧХ – рисунок 5, разомкнутой системы:

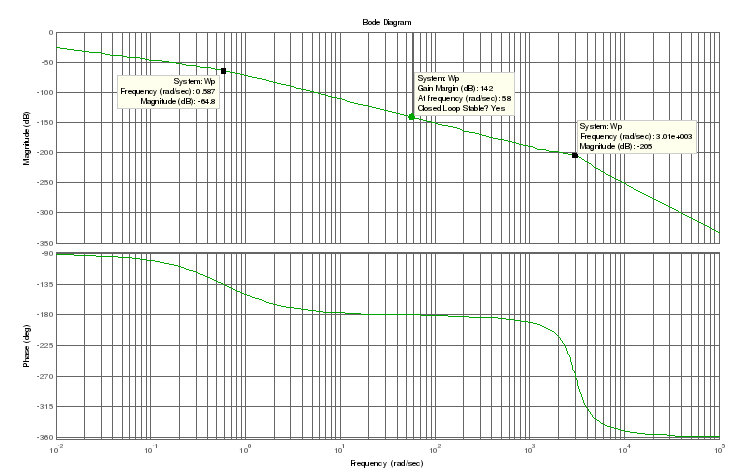
Рисунок 5 – ЛАЧХ и ЛФЧХ разомкнутой системы

15

УИТС.421243.010 ПЗ

4.2 Построение ЖЛАЧХ

Проведем построение ЖЛАЧХ методом запретной зоны желаемой

называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. ЖЛАЧХ состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной. Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики.

Перейдем к дискретной системе с периодом дискретизации T=0.0005 c

(20)

Л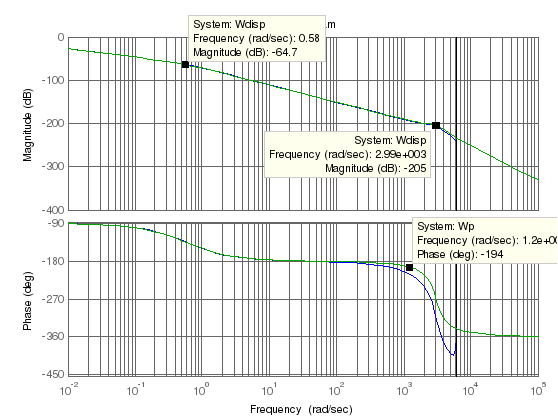АЧХ дискретной модели строится в зависимости от псевдочастоты λ, при этом сначала проводится ω-преобразование заменяя z=(1+ω)/(1-ω), а затем осуществляется переход от W(ω) к частотному выражению передаточной функции через псевдочастоту λ путем замены ω=0.5Tλj.