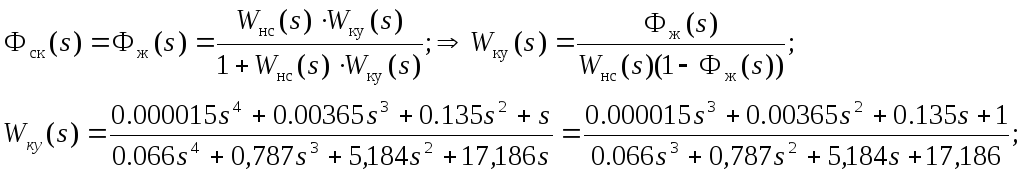5. Кривая d-разбиения в плоскости одного параметра.

Построим кривую D-разбиения по параметру k_у.

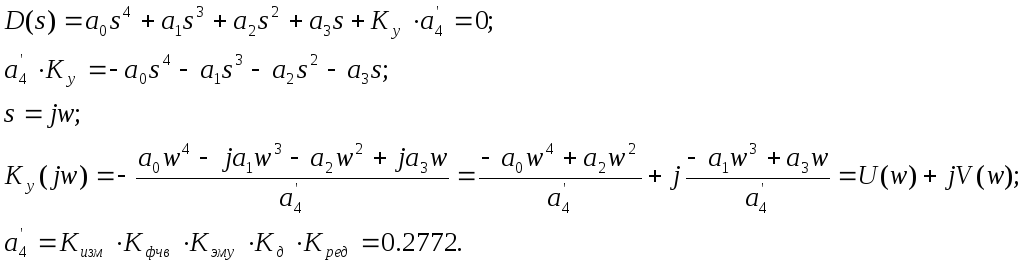
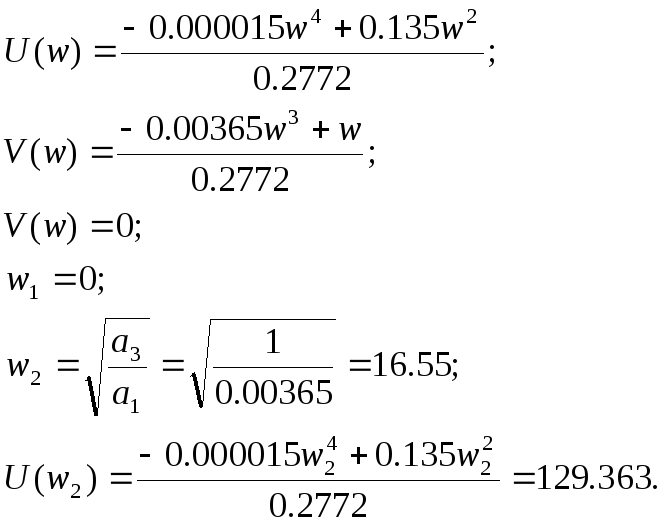
Таблица 7.

w	U(w)	V(w)
-25	283,2454	-115,5528499
-20	186,1472	-33,18903319
-15	106,8385	9,672619048
-10	48,16017	22,90764791
-5	12,1415	16,39159452
0	0	0
5	12,1415	-16,39159452
10	48,16017	-22,90764791
15	106,8385	-9,672619048
20	186,1472	33,18903319
25	283,2454	115,5528499

129,36

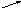
Рис. 10. Кривая D-разбиения.

Область I является претендентом на область устойчивости замкнутой системы. Пусть К_у=50. Проверим устойчивость замкнутой системы по критерию Гурвица.

Характеристический полином замкнутой системы:

Определитель Гурвица:

Так как все определители положительны, то система устойчива. Значит, область I является областью устойчивости замкнутой системы.

6. Оценка запасов устойчивости системы по модулю и по фазе.

Оценим запасы устойчивости системы по модулю и по фазе, пользуясь критерием Найквиста.

Рис. 11. График АФХ разомкнутой системы W(jw).

Запас устойчивости системы по модулю: m=0.2;

Запас устойчивости системы по фазе: =18.

7. Лах и лфх разомкнутой системы. Оценка запасов устойчивости системы.

Построим ЛАХ и ЛФХ разомкнутой системы в Matlab.

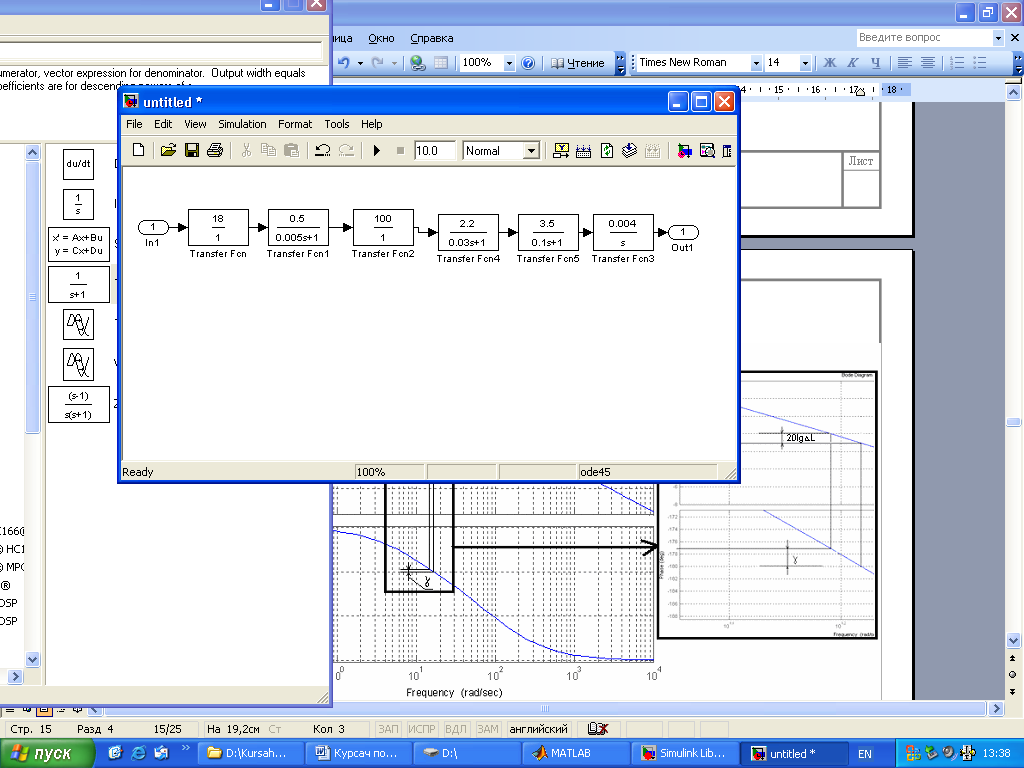
Рис. 12. Структурная схема разомкнутой системы.

Рис. 13. ЛАХ и ЛФХ разомкнутой системы.

Запас устойчивости системы по модулю: 20 lg L=-1; m=1-L =0.11;

Запас устойчивости системы по фазе: =8.

8. График переходной функции заданной нескорректированной системы. Оценка показателей качества нескорректированной системы.

Построим график переходной функции h(t) заданной нескорректированной системы в приложении Simulink пакета Matlab.

Рис. 14. Структурная схема замкнутой системы.

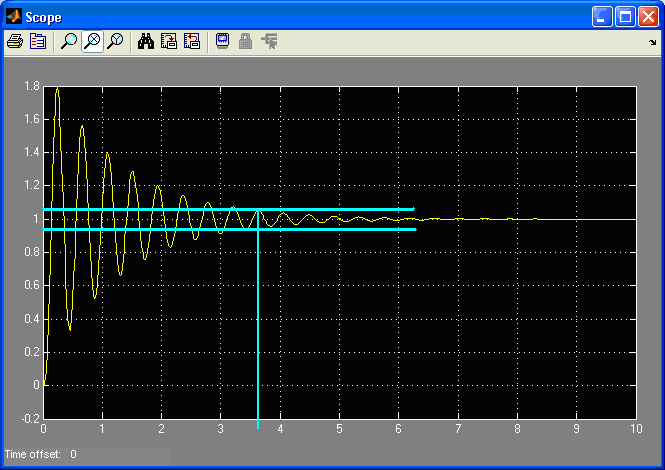
Рис. 15. Переходный процесс нескорректированной системы (сходящийся).

Показатели качества нескорректированной системы:

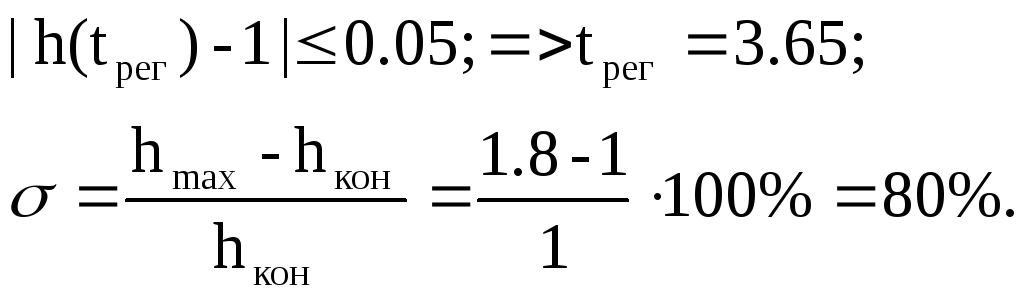
Полученные значения показателей качества нескорректированной системы не удовлетворяют требуемым (t_рег<=1.2; <=20%).

9. Синтез последовательного корректирующего устройства методом Соколова.

Проведем синтез последовательного корректирующего устройства методом Соколова.

Передаточная функция нескорректированной системы:

1). Определяем разность порядков полиномов числителя (m₁) и знаменателя (n₁) передаточной функции замкнутой нескорректированной системы (n₁-m₁):

Формируем желаемую передаточную функцию замкнутой системы, на основе нормированных передаточных функций. Заданный порядок астатизма системы: ν_зад=1.

Нормированная функция имеет вид:

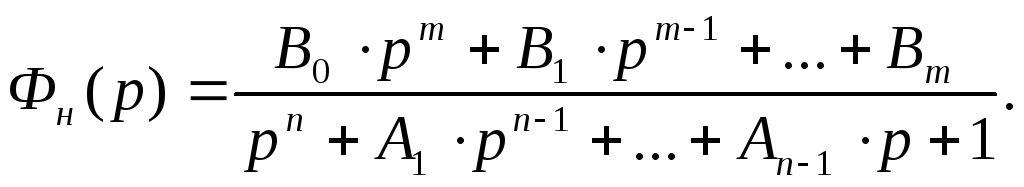
Определяем порядок числителя и знаменателя нормированной передаточной функции:

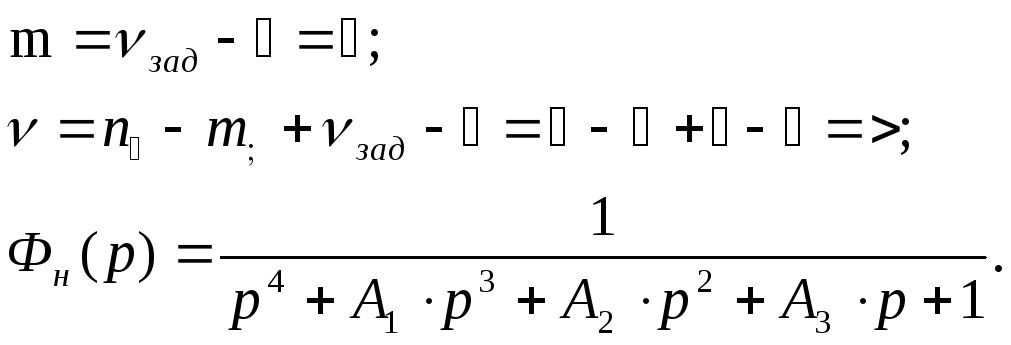
2). Коэффициенты нормированной передаточной функции для критического затухания переходного процесса выбираем исходя из показателей качества. Т.к. в условиях дано, что t_рег=1,2 , то воспользуемся приложением А, таблицей А.1, из которой определим значения коэффициентов, а также нормированное время : 1; 2.6; 3.8; 2.8; 1; τ_н=4.5.

Желаемая передаточная функция выбирается с использованием теоремы масштабов преобразования Лапласа:

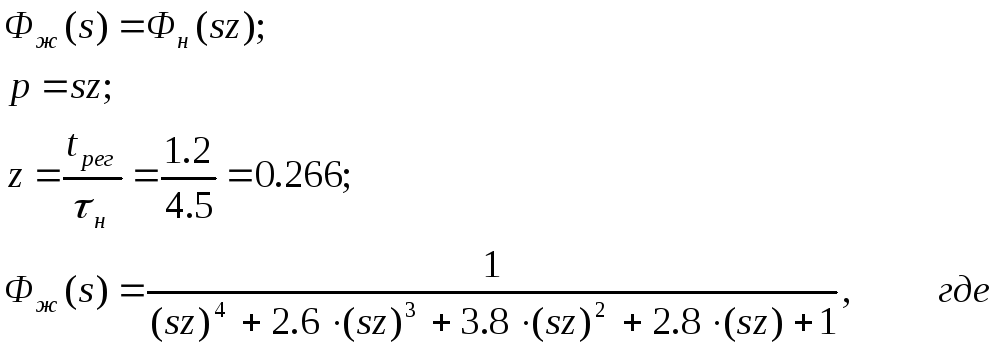
p – аргумент нормированной передаточной функции,

s – комплексный аргумент Лапласа,

z – коэффициент масштаба времени,

t_рег – заданное время регулирования,

– время регулирования нормированной передаточной функции.

Определяем желаемую передаточную функцию:

3). Определим корректирующее устройство: