4.3 Передаточная функция системы терморегулирования с настроенным регулятором

Передаточная функция разомкнутой системы

.

Тогда передаточная функция замкнутой системы примет вид

.

Характеристический полином замкнутой системы

.

5 Исследование устойчивости системы терморегулирования

5.1 Оценка устойчивости при помощи алгебраического критерия устойчивости Гурвица

При исследовании устойчивости системы с использованием алгебраического критерия устойчивости Гурвица рассматривается характеристический полином замкнутой системы. По Гурвицу для устойчивой системы должны соблюдаться два условия:

1. коэффициенты характеристического полинома должны быть положительными;

2. должны быть положительными определители, составленные из этих коэффициентов [1].

Характеристический полином замкнутой системы

.

1) ,

,

,

.

2)Для системы третьего порядка

Оба условия критерия выполняются, следовательно, данная система устойчива.

5.2 Построение области устойчивости системы методом d-разбиения

Область устойчивости строится в плоскости двух задаваемых параметров системы и. Для выполнения исследования необходимо найти характеристический комплекс системы. Запишем характеристический полином замкнутой системы

,

.

Так как и, то.

Тогда, подставив числовые значения,

,

.

Преобразуем последнее выражение в характеристический комплекс, для этого вместо подставим

Найдем параметрические уравнения границы устойчивости

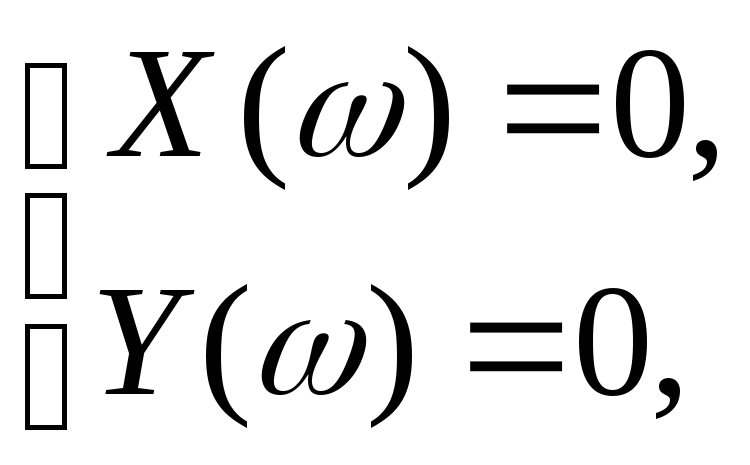
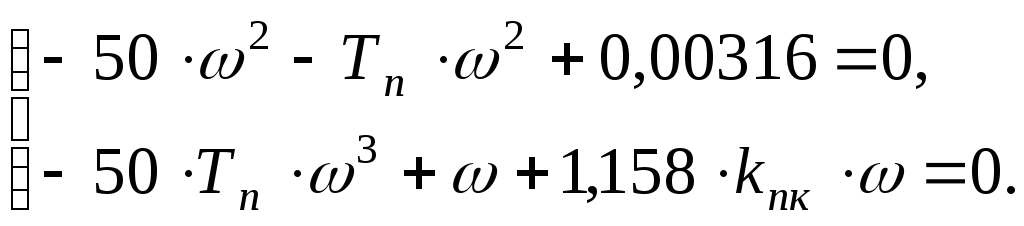
Выразим и:

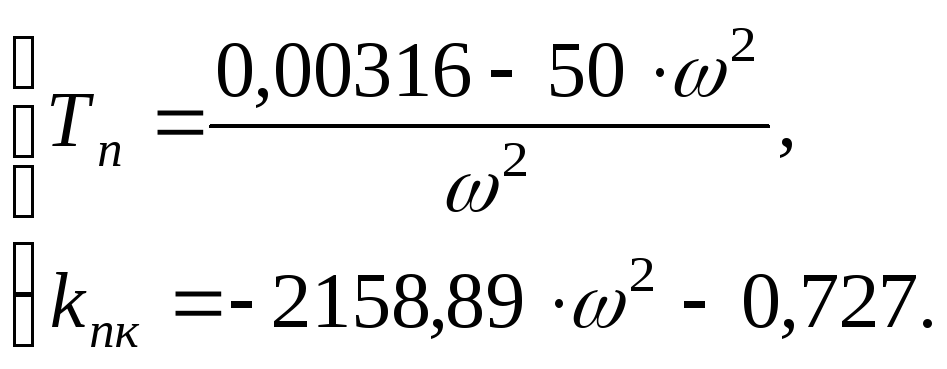
Выражения в полученной системе являются параметрическими уравнениями границы устойчивости. Исследуем ход кривой, выявив ее особые точки. Характерными точками прямой являются точки разрыва и точки пересечения ее осей координат [1].

Найдем точки разрыва:

, .

Найдем точки пересечения осей координат:

, т.е. прикривая пересекает ось,

кривая не пересекает ось .

Задаем ряд значений частоты в пределах. Так как частотавходит в параметрические выражения границы области устойчивости в четной степени, то достаточно рассмотреть только область положительных частот. Зависимостииотображены в таблице 6.

Таблица 6

0,006	37,77778	-0,80472
0,0065	24,7929	-0,81821
0,007	14,4898	-0,83279
0,0075	6,177778	-0,84844
0,008	-0,625	-0,86517
0,0085	-6,26298	-0,88298
0,009	-10,9877	-0,90187
0,0095	-14,9861	-0,92184
0,01	-18,4	-0,94289
0,012	-28,0556	-1,03788
Продолжение таблицы 6
0,014	-33,8776	-1,15014
0,016	-37,6563	-1,27968
0,018	-40,2469	-1,42648
0,02	-42,1	-1,59056
0,03	-46,4889	-2,67
0,04	-48,025	-4,18122
0,05	-48,736	-6,12423
0,06	-49,1222	-8,499
0,07	-49,3551	-11,3056
0,08	-49,5063	-14,5439
0,09	-49,6099	-18,214
0,1	-49,684	-22,3159

Определяем дополнительные границы области устойчивости приравниванием к нулю первого коэффициента характеристического многочлена и его свободного члена [1]:

Определяем расположение области устойчивости относительно границ с использованием правила штриховки. Для этого составляем определитель вида [1]

.

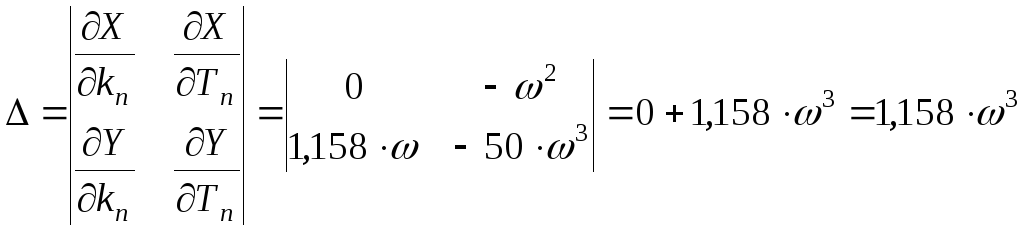Исследуем знак определителя. Если , тодвигаясь в направлении, область штрихуется справа, а если, тодвигаясь в направлении, область штрихуется слева.

График области устойчивости системы представлен на рисунке 9.

Проверяем настроенную систему терморегулирования с помощью контрольной точки A(). ТочкаA(16,7; 6144) попадает в построенную область устойчивости.