4 Расчет настроек пропорционально-интегрального регулятора

4.1 Построение логарифмических частотных характеристик

Для расчета настроек регулятора используем метод логарифмических частотных характеристик системы (ЛЧХ). Исходным для построений является выражение передаточной функции разомкнутой системы

.

Сначала построим ЛЧХ для системы без учета регулятора. Передаточная функция такой системы

.

Из данной передаточной функции найдем частоты сопряжения

,

,

и ординату единичной частоты

.

График логарифмической амплитудной характеристики (ЛАХ) для системы без учета регулятора имеет 3 участка:

1. Низкочастотный участок (). Так как показатель астатизма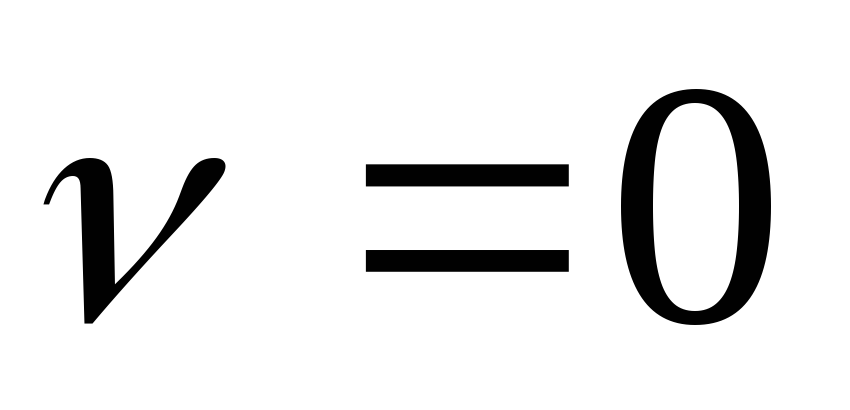, наклон ЛАХ составляет.

2. Среднечастотный участок (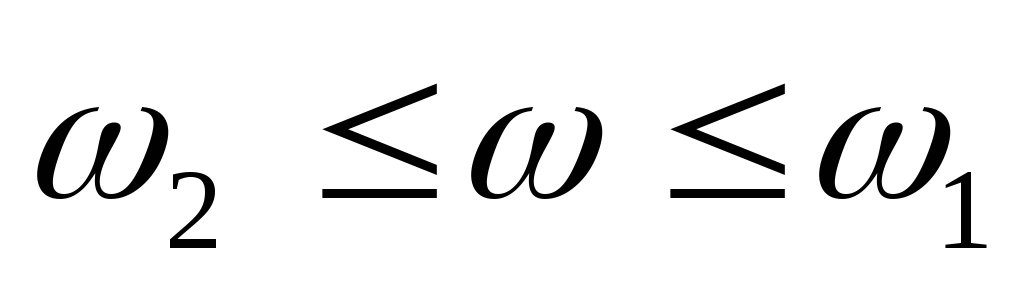). Начинает влиять инерционность электрической печи и наклон ЛАХ уже становится.

3. Высокочастотный участок (). Начинает влиять инерционность термопары и наклон ЛАХ в конечном итоге составляет.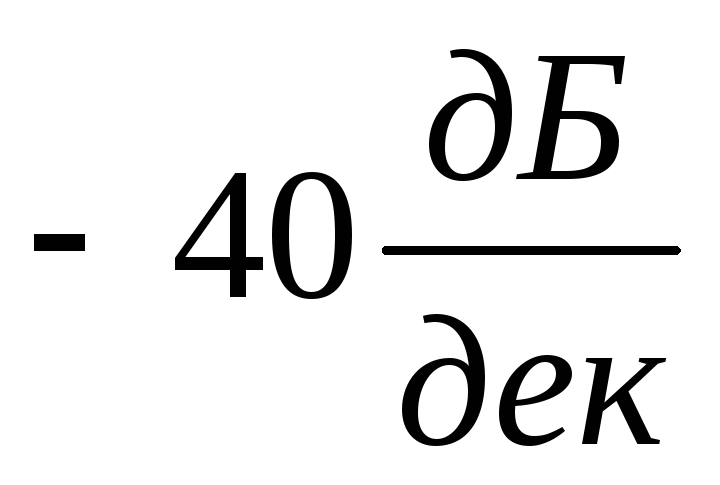

График ЛАХ для системы без учета регулятора изображен кривой на рисунке 8.

Логарифмическая фазовая характеристика (ЛФХ) для системы без учета регулятора

,

или, подставив значения,

.

Значения для построения ЛФХ приведены в таблице 3.

Таблица 3

0	0
0,0001	-32
0,000163	-46
0,0002	-51
0,0003	-62
0,0004	-69
0,0005	-73
0,0006	-77
0,0007	-79
0,0008	-81
0,0009	-82
0,001	-84
0,002	-91
0,003	-95
0,004	-99
0,005	-102
0,006	-105
0,007	-108
0,008	-111
0,009	-113
0,01	-116
0,02	-135
0,03	-146
0,04	-153
0,05	-158
0,06	-161
0,07	-164
0,08	-166
0,09	-167
0,1	-169
0,2	-174
0,3	-176
0,4	-177
0,5	-178
0,6	-178
0,7	-178
0,8	-179
0,9	-179
1	-179

График ЛФХ для системы без учета регулятора изображен кривой на рисунке 8.

4.2 Определение настроек регулятора

Наибольшее влияние на динамику системы оказывают инерционные свойства печи. Это влияние можно скомпенсировать за счет ПИ-регулятора, который является форсирующим звеном первого порядка. Выберем постоянную времени регулятора равную постоянной времени печи.

.

Тогда передаточная функция разомкнутой системы

.

Следовательно, логарифмическая амплитудная характеристика на низкочастотном участке будет иметь наклон, на среднечастотном, на высокочастотном.

Логарифмическая фазовая характеристика для системы с учетом регулятора рассчитывается по формуле

,

или, подставив значения,

.

Значения для построения ЛФХ приведены в таблице 4.

Таблица 4

0	-90
0,0001	-122
0,000163	-136
0,0002	-141
0,0003	-152
0,0004	-159
0,0005	-163
0,0006	-167
0,0007	-169
0,0008	-171
0,0009	-172
0,001	-174
Продолжение таблицы 4
0,002	-181
0,003	-185
0,004	-189
0,005	-192
0,006	-195
0,007	-198
0,008	-201
0,009	-203
0,01	-206
0,02	-225
0,03	-236
0,04	-243
0,05	-248
0,06	-251
0,07	-254
0,08	-256
0,09	-257
0,1	-259
0,2	-264
0,3	-266
0,4	-267
0,5	-268
0,6	-268
0,7	-268
0,8	-269
0,9	-269
1	-269

Графики логарифмической фазовой и логарифмической амплитудной характеристик для системы с учетом регулятора изображены кривыми исоответственно на рисунке 8.

Так как на среднечастотном участке кривая имеет наклон, то в системе возникает колебательный процесс. Следовательно, появляется перерегулирование в системе, ухудшаются ее свойства. Поэтому колебательный процесс нежелателен для системы. Чтобы избавиться от колебательного процесса, необходимо построить ЛАХ, наклон которой на среднечастотном участке составляет. График логарифмической амплитудной характеристики изображен кривойна рисунке 8.

Логарифмическая фазовая характеристика для системы с учетом регулятора рассчитывается по формуле

,

или, подставив значения,

.

Значения для построения ЛФХ приведены в таблице 5.

Таблица 5

0	-90
0,0001	-90
0,000163	-90
0,0002	-91
0,0003	-91
0,0004	-91
0,0005	-91
0,0006	-92
0,0007	-92
0,0008	-92
0,0009	-93
0,001	-93
0,002	-96
0,003	-99
0,004	-101
0,005	-104
0,006	-107
0,007	-109
0,008	-112
0,009	-114
0,01	-117
0,02	-135
0,03	-146
0,04	-153
0,05	-158
0,06	-162
0,07	-164
Продолжение таблицы 5
0,08	-166
0,09	-167
0,1	-169
0,2	-174
0,3	-176
0,4	-177
0,5	-178
0,6	-178
0,7	-178
0,8	-179
0,9	-179
1	-179

График логарифмической фазовой характеристики изображен кривой на рисунке 8.

Чтобы достичь наиболее благоприятного процесса, необходимо, чтобы желаемая частота среза лежала левее. Для этого отложим от0,8 декады и получим. Через полученную частоту проведем ЛАХ системы с настроенным регуляторомпараллельно. В данном случае ЛФХ не изменится, т.е..

По графику определяем .

,

где - коэффициент усиления разомкнутой системы.

Отсюда .

Общий коэффициент усиления настроенной системы

,

где - коэффициент усиления интегрального канала.

Тогда

.

Из формулы найдем коэффициент усиления пропорционального канала

.

По найденным значениям коэффициентов усиления пропорционального и интегрального каналов регулятора рассчитываем элементы операционных усилителей У4 и У5.

Операционный усилитель У4 является пропорциональным каналом регулятора. Коэффициент усиления пропорционального канала

.

Из ряда стандартных сопротивлений Е24 [3] выбираем кОм.

Тогда

кОм.

Для того, чтобы обеспечить нужное значение , необходимо разбить резисторна постоянныйи переменный

кОм,

кОм.

Из ряда стандартных сопротивлений Е24 [3] выбираем кОм,кОм.

Операционный усилитель У5 представляет собой интегратор. Передаточная функция интегрирующего звена

.

Так как , то

.

Следовательно,

.

Предположим, что мкФ, тогда

Ом

Необходимо разбить резистор на постоянныйи переменный

Ом,

Ом.

Из ряда стандартных сопротивлений Е24 [3] выбираем МОм,кОм