
- •Устойчивость систем автоматического управления Понятие устойчивости системы
- •Критерии устойчивости
- •Алгебраический критерий устойчивости Раусса. 1875г.
- •Критерий устойчивости Гурвица. 1895 г.
- •О критическом коэффициенте усиления
- •Частотные критерии устойчивости
- •Принцип аргумента
- •Критерий устойчивости Михайлова
- •Частотный критерий устойчивости Найквиста
- •Обобщенная формулировка критерия Найквиста
- •Логарифмический критерий устойчивости (Найквиста)
- •О применении критериев устойчивости
Критерий устойчивости Михайлова
Характерной особенностью данного метода является то, что об устойчивости системы судят по поведению годографа Михайлова исследуемой системы:
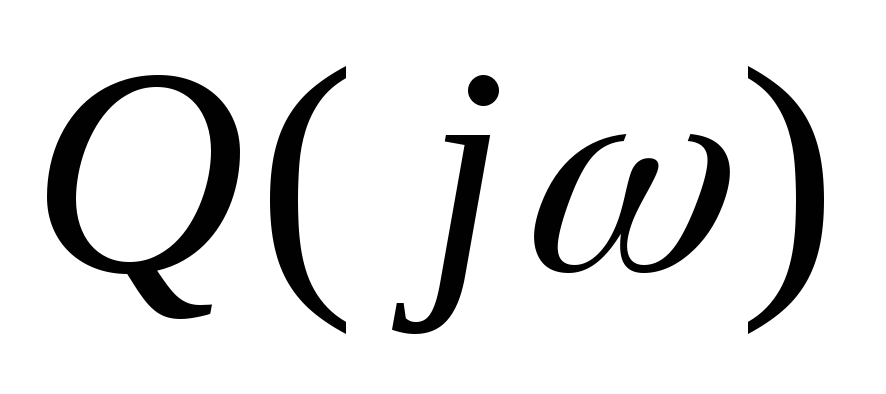 - для разомкнутой системы;
- для разомкнутой системы;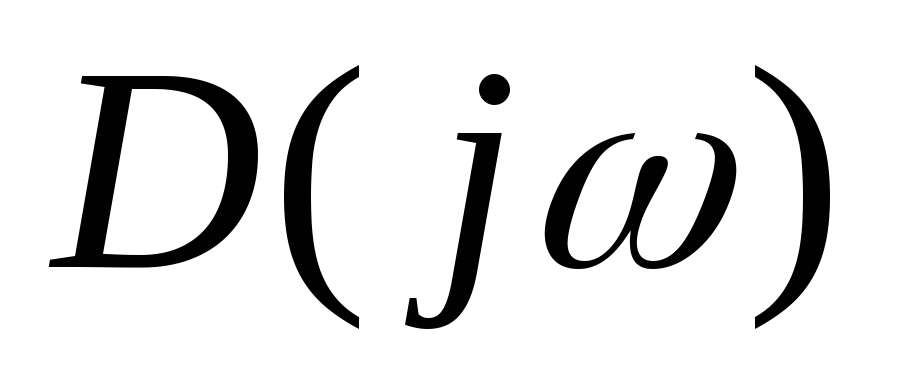 - для замкнутой системы.
- для замкнутой системы.
Под годографомпонимается кривая, которую описывает
конец вектора![]() или
или![]() на комплексной плоскости при измененииот 0 до
на комплексной плоскости при измененииот 0 до![]() .
Здесь
.
Здесь![]() и
и![]() - полиномы знаменателей соответствующих
передаточных функций.
- полиномы знаменателей соответствующих
передаточных функций.
На основании принципа аргумента формулируется критерий Михайлова:
Для устойчивости системы необходимо и
достаточно, чтобы годограф вектора
Михайлова
![]() для замкнутой и
для замкнутой и![]() для разомкнутой системы) при измененииот 0до +
повернулся в положительном направлении
на угол(/2)n
или, иначе, пересек по очередиn
квадратов без пропусков.
для разомкнутой системы) при измененииот 0до +
повернулся в положительном направлении
на угол(/2)n
или, иначе, пересек по очередиn
квадратов без пропусков.
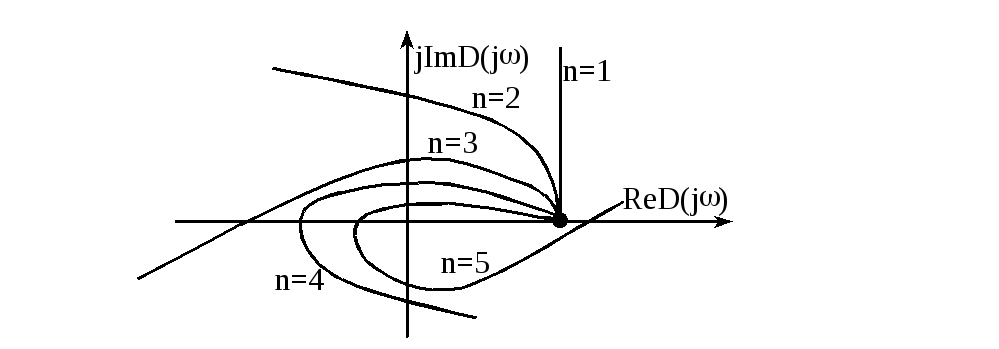
Все эти годографы (и системы соответственно) устойчивы.
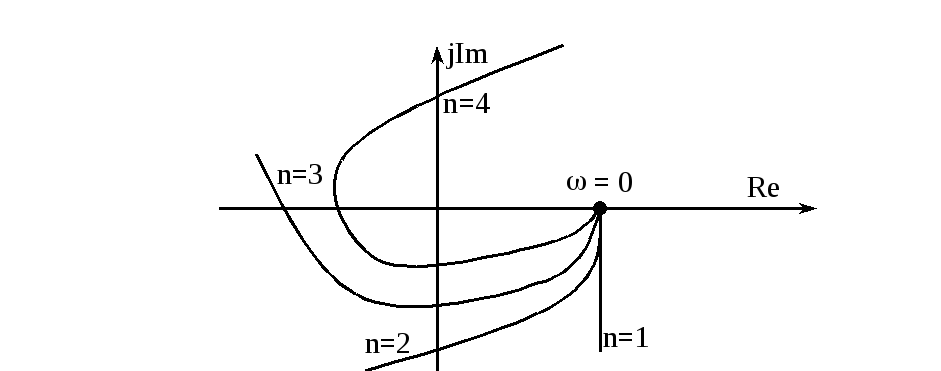
Эти системы неустойчивы, так как вектор годографа Михайлова вращается в отрицательном направлении.
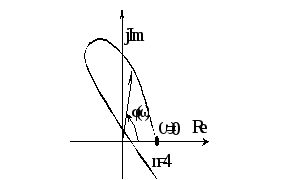
Система неустойчива, так как квадранты проходятся непоследовательно.
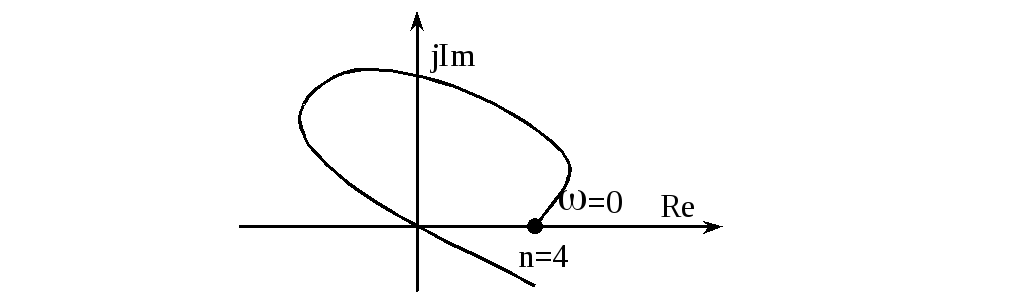
Система находиться на границе устойчивости. При подсчете порядка системы каждое прохождение годографа через 0 повышает порядок на 1.
Следствие из критерия Михайлова:
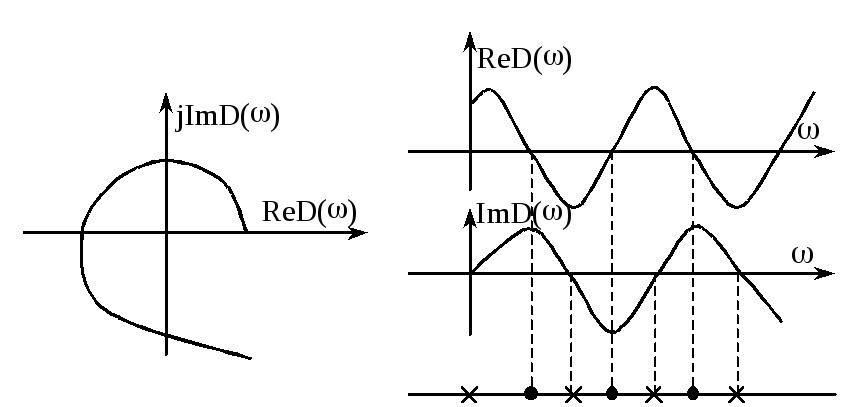
Для устойчивости системы необходимо и достаточно, чтобы корни мнимой и вещественной частей годографа Михайлова перемежались.
Если корни не перемежаются, то система неустойчива.
Если характеристическое уравнение
![]() не имеет какого либо члена, то система
также неустойчива.
не имеет какого либо члена, то система
также неустойчива.
Частотный критерий устойчивости Найквиста
Частотный
критерий Найквиста дает возможность
определить устойчивость замкнутой
системы по АФЧХ ее разомкнутой цепи
(разомкнутой системы) ![]() .
Ниже показано, как определяется
передаточная функция разомкнутой
системы
.
Ниже показано, как определяется
передаточная функция разомкнутой
системы![]() для
случая единичной и неединичной обратной
связи.
для
случая единичной и неединичной обратной
связи.

Следовательно,
об устойчивости замкнутой системы с
передаточной функцией
![]() будем судить по передаточной функции
разомкнутой системы
будем судить по передаточной функции
разомкнутой системы ![]() ,
а именно по поведению годографа
,
а именно по поведению годографа![]() .
.
Рассмотрим вспомогательную передаточную функцию
![]() , где обозначено
, где обозначено![]() .
.
Пусть порядок
полинома
![]() равенn
и порядок полинома
равенn
и порядок полинома![]() ,
причем
,
причем![]() (в основном так и бывает). Тогда порядок
полинома
(в основном так и бывает). Тогда порядок
полинома![]() также будет равенn.
Различают три возможных
ситуации:
также будет равенn.
Различают три возможных
ситуации:
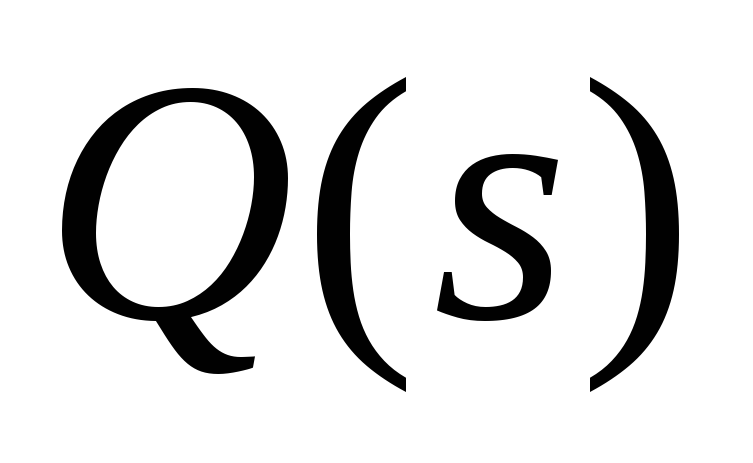 не
содержит правых или нулевых корней, то
есть разомкнутая система устойчива.
не
содержит правых или нулевых корней, то
есть разомкнутая система устойчива.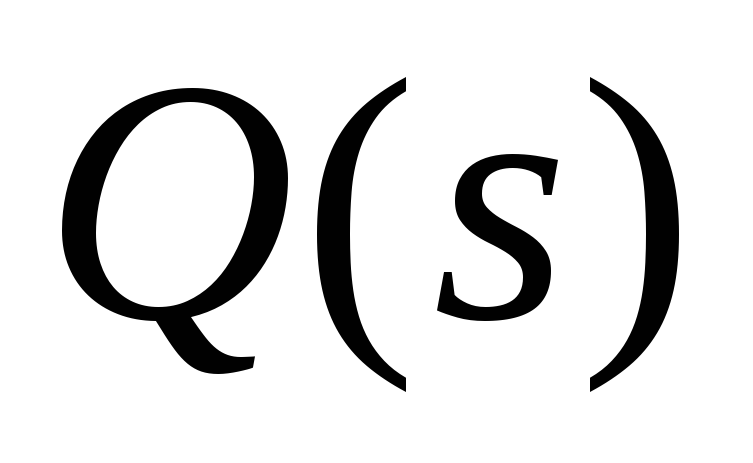 имеет
хотя бы один правый корень, следовательно,
система в разомкнутом состоянии
неустойчива.
имеет
хотя бы один правый корень, следовательно,
система в разомкнутом состоянии
неустойчива.Все корни
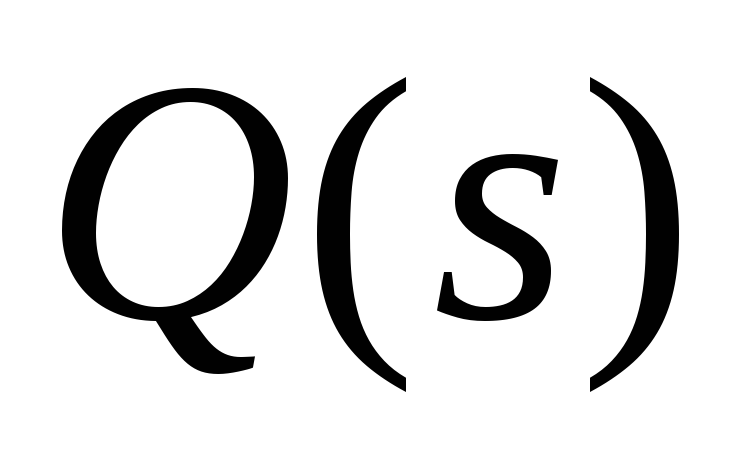 левые,
но есть и корни на мнимой оси (нейтральная
система).
левые,
но есть и корни на мнимой оси (нейтральная
система).
Задача.Определить условия, при которых в замкнутом состоянии система будет устойчива в каждом из трех случаев.
Случай 1.Число правых корней равно 0. Все корни - левые. Разомкнутая система устойчива.
![]() .
Для устойчивости замкнутой системы
(это наше требование) необходимо, что
все корни полинома
.
Для устойчивости замкнутой системы
(это наше требование) необходимо, что
все корни полинома![]() - левые, то есть
- левые, то есть![]() .
.
Применим к
![]() принцип аргумента. При изменении
принцип аргумента. При изменении![]() от 0 до
от 0 до![]() изменение величины фазового сдвига
составляет (в соответствии с правилами
деления комплексных чисел):
изменение величины фазового сдвига
составляет (в соответствии с правилами
деления комплексных чисел):
![]() .
.
При устойчивой
замкнутой системе приращение
![]() .
.
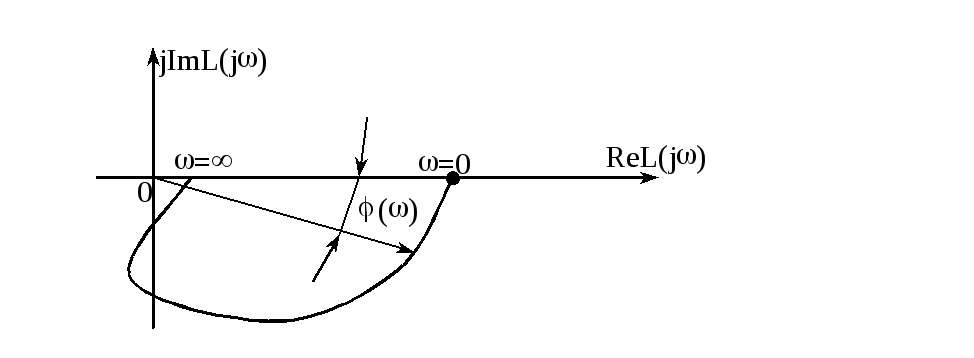
Получили кривую ![]() ,
не охватывающую начало координат:
,
не охватывающую начало координат:
Если учесть, что
![]() ,
следовательно
,
следовательно![]() ,
или
,
или![]() .
Таким образом в плоскости
.
Таким образом в плоскости![]() получаем:
получаем:
Точка (![]() )
на плоскости
)
на плоскости![]() преобразовалась в точку (
преобразовалась в точку (![]() ) на плоскости
) на плоскости![]() .
.
Вывод.
Для устойчивости замкнутой системы,
устойчивой в разомкнутом состоянии
необходимо и достаточно, чтобы годограф
АФЧХ разомкнутой системы при изменении![]() от 0 до
от 0 до![]() не охватывал критическую точку с
координатой (
не охватывал критическую точку с
координатой (![]() ).
).
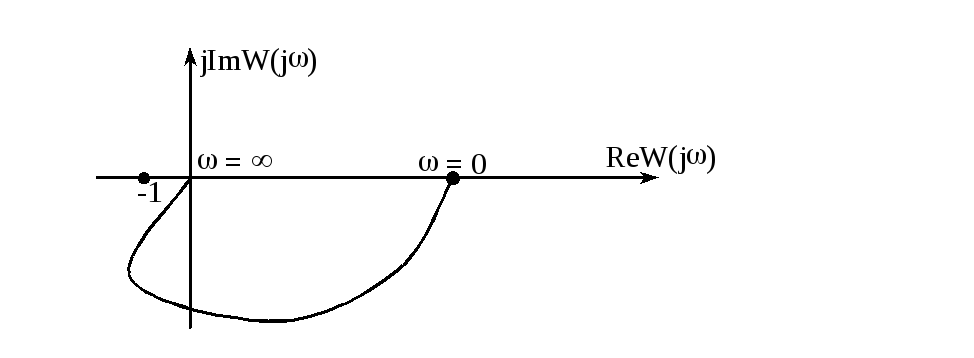
На рисунке приведены годографы разомкнутых систем, устойчивых и в замкнутом состоянии.
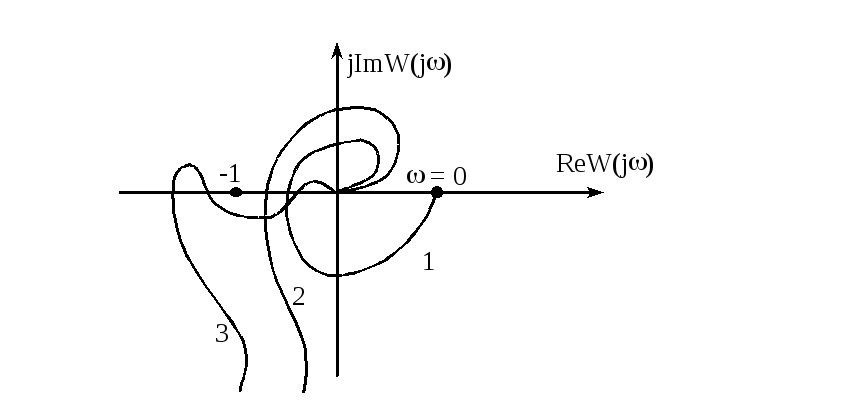
Характеристики, обозначенные цифрами 1 и 2, соответствуют системам, устойчивым как в разомкнутом, так и в замкнутом состоянии. Для этих систем уменьшение коэффициента усиления отодвигает характеристику от опасной зоны. Характеристика 3 - условно устойчивая система. В условно устойчивой системе уменьшение коэффициента усиления может привести к неустойчивости замкнутой системы.
На следующем рисунке приведен годограф системы, неустойчивой в замкнутом состоянии.
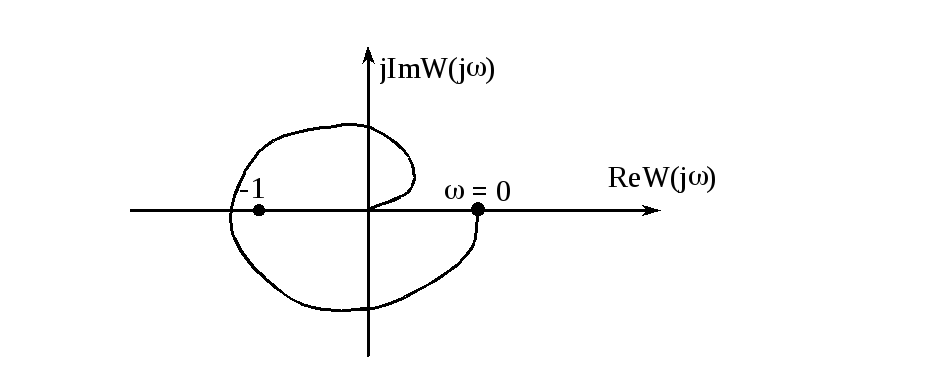
При ![]() выходной сигнал отстает от сигнала на
входе системы на 1800, то есть
находится с ним в противофазе. Если
выходной сигнал отстает от сигнала на
входе системы на 1800, то есть
находится с ним в противофазе. Если![]() =1
(как на рисунке), то при замыкании системы
с ООС сигналx0,
равный алгебраической суммеq
иy,
не будет ни усиливаться, ни ослабляться.
Система будет находиться на границе
устойчивости.
=1
(как на рисунке), то при замыкании системы
с ООС сигналx0,
равный алгебраической суммеq
иy,
не будет ни усиливаться, ни ослабляться.
Система будет находиться на границе
устойчивости.
Если
![]() ,
то сигнал будет циклически усиливаться.
Система становится неустойчивой, даже
если снять входной сигнал.
,
то сигнал будет циклически усиливаться.
Система становится неустойчивой, даже
если снять входной сигнал.
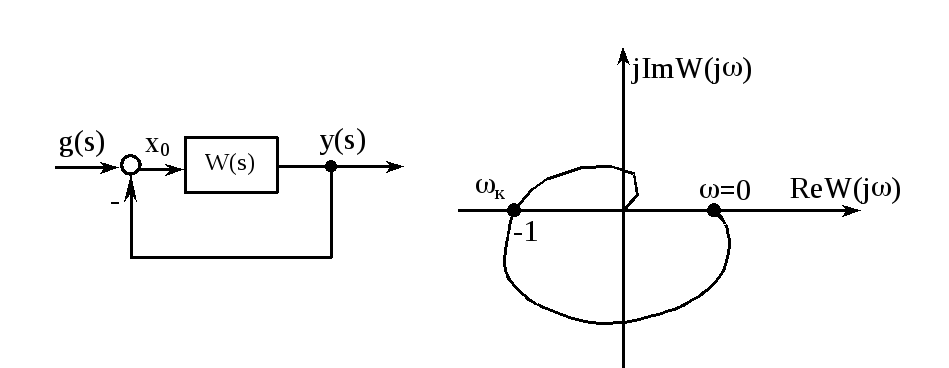
Случай 2. Система в разомкнутом состоянии неустойчива.
Полином
![]() имеетm1
правых корней,
n-m1- левых. На основании
принципа аргумента:
имеетm1
правых корней,
n-m1- левых. На основании
принципа аргумента:
![]() .
.
Следовательно,
для устойчивости замкнутой системы,
неустойчивой в разомкнутом состоянии,
необходимо и достаточно, чтобы годограф
АФЧХ разомкнутой системы при измененииот 0 до![]() ,
двигаясь в положительном направлении
(против часовой стрелки),
,
двигаясь в положительном направлении
(против часовой стрелки),![]() раз охватил критическую точку
раз охватил критическую точку![]() .
.
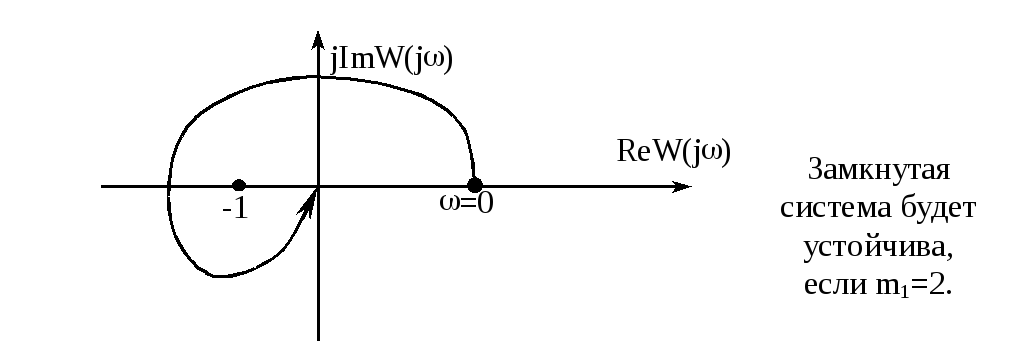 Случай
3. В разомкнутом состоянии имеются
корни на мнимой оси (нулевые корни).
Случай
3. В разомкнутом состоянии имеются
корни на мнимой оси (нулевые корни).
Передаточная
функция разомкнутой системы
![]() причем
причем![]() ,
или
,
или ![]() .
Пустьr
=1. Если нулевой корень сдвинуть
влево на малую величину
.
Пустьr
=1. Если нулевой корень сдвинуть
влево на малую величину
![]() ,
тогда передаточная функция примет
вид
,
тогда передаточная функция примет
вид![]() ,
а частотная характеристика будет
определяться выражением
,
а частотная характеристика будет
определяться выражением![]() .
Дальнейшие рассуждения при получении
критерия устойчивости базируются на
рассмотренном выше случае 1:
.
Дальнейшие рассуждения при получении
критерия устойчивости базируются на
рассмотренном выше случае 1:
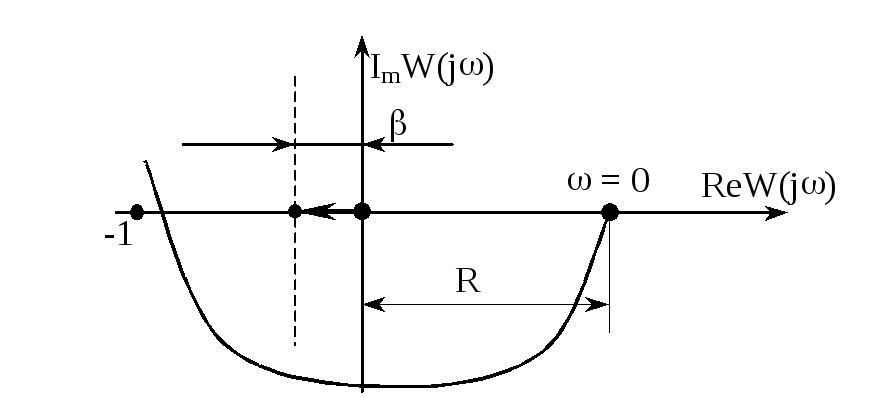
Начальный
радиус точки при ![]() есть
есть
![]() .
Если устремить
.
Если устремить
![]() ,
то начальное значение АФЧХ также
изменится:
,
то начальное значение АФЧХ также
изменится:![]() .
Следовательно, предельное стягивание
корня на свое исходное положение
обеспечивает увеличение начального
радиуса до
.
Следовательно, предельное стягивание
корня на свое исходное положение
обеспечивает увеличение начального
радиуса до![]() ,
но интегрирующее звено обеспечивает
сдвиг по фазе на угол -900.
,
но интегрирующее звено обеспечивает
сдвиг по фазе на угол -900.
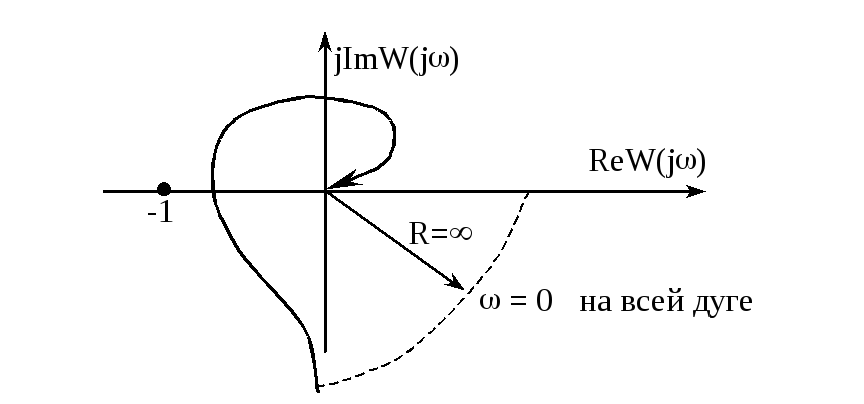
Вывод. Для устойчивости замкнутой
системы, имеющем в разомкнутом состоянии
все левые точки, а также 1 или несколько
нулевых корней, необходимо и достаточно,
чтобы при изменении
от 0 до
![]() критическая точка
критическая точка
![]() не охватывалась годографом АФЧХ
разомкнутой системы вместе с ее
дополнением.
не охватывалась годографом АФЧХ
разомкнутой системы вместе с ее
дополнением.
Дополнением является дуга с ![]() ,
повернутая от оси вещественных корней
на угол
,
повернутая от оси вещественных корней
на угол
![]() .
.
