4.2.7. Отдельные задачи теплопроводности при стационарном режиме

В технике часто возникают задачи определения температурного поля тела и установления законов передачи теплоты. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье  соответствующие тепловые потоки. Следует отметить, что аналитическое решение поставленной задачи возможно только для тел правильной геометрической формы и при достаточно простых условиях однозначности. В остальных случаях эта задача решается численными или экспериментальными методами.

Рассмотрим несколько тел простой формы — таких, как плоская стенка и полая труба — в случае стационарного распространения теплоты, для которых уравнение теплопроводности значительно упрощается.

4.2.7.1. Теплопроводность через плоскую и цилиндрическую стенки.

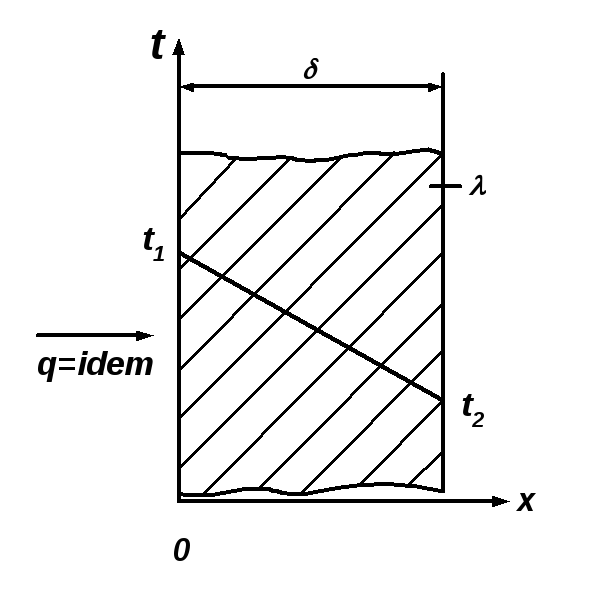
Рассмотрим однородную плоскую однослойную стенку толщиной , (рис. 4.4), имеющую неограниченную длину и ширину.

На наружных поверхностях стенки поддерживаются постоянные температуры t₁ и t₂. Коэффициент теплопроводности стенки постоянен и равен . При стационарном режиме t=0 и отсутствии внутренних источников теплоты q_v=0 и с учетом того, что в этом случае температура будет изменяться только в направлении оси ОХ, дифференциальное уравнение теплопроводности примет вид

(4.22)

Интегрируя уравнение (4.22), находим

(4.23)

Рис. 4.4. Температурное поле плоской однослойной стенки

После второго интегрирования получаем общий вид уравнения распределения температур в плоских стенках:

t=C₁x+C₂. (4.24)

Постоянные С₁ и С₂ в уравнении (2.24) определяются из граничных условий:

при х=0 t=t₁, C₂=t₁;

при х= t=t₂,

Подставляя значения постоянных С₁ и С₂ в уравнение (4.24), получаем уравнение распределения температуры в рассматриваемой плоской однослойной стенке

(4.25)

Уравнение (4.25) является уравнением прямой линии.

Плотность теплового потока, проходящего через стенку в соот-ветствии с законом Фурье, q = t/n. Учитывая, что

, получим . (4.26)

Отношение / (Вт/(м²К)) называется тепловой проводимостью стенки, а обратная величина / (м²К/Вт) — тепловым или термическим сопротивлением стенки. Последнее представляет собой изменение температуры в стенке на единицу плотности теплового потока.

Тепловой поток, который передается через полную поверхность стенки,

, Вт. (4.27)

Для многослойных стенок уравнение имеет вид

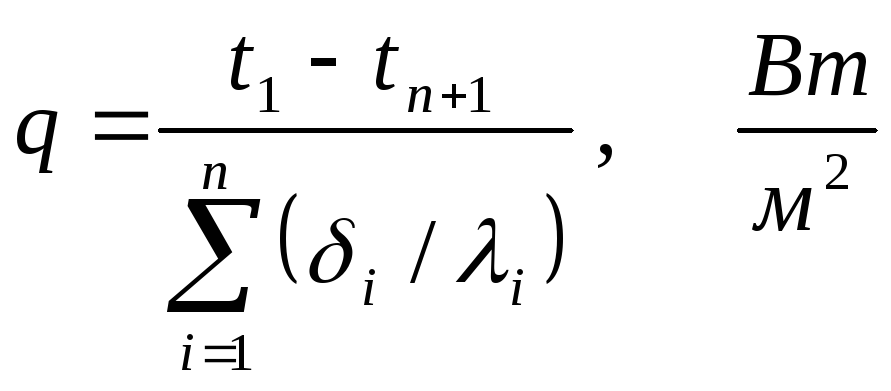. (4.28)

Величина называется полным термическим сопротивлением теплопроводности многослойной стенки.

При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности _экв многослойной стенки. Он равен коэффициенту теплопроводности однородной стенки, толщина которой  равна толщине многослойной стенки , а термическое сопротивление равно термическому сопротивлению рассматриваемой стенки, т.е.:

.

Отсюда

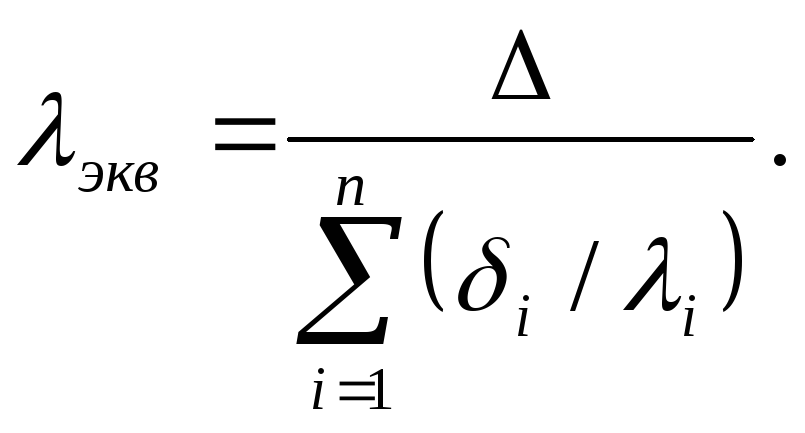(4.29)

Из уравнения (4.29) следует, что эквивалентный коэффициент теплопроводности _экв зависит не только от теплофизических свойств слоев, но и от их толщины.

Графически распределение температур по сечению многослойной стенки представляется ломаной линией; температуры на границе соприкосновения слоев можно определить уравнением

(4.30)

При рассмотрении стационарного процесса теплопроводности в цилиндрической однослойной стенке (трубе) с внутренним радиусом r₁ и наружным r₂ (рис. 4.5) получаем уравнение распределения температуры:

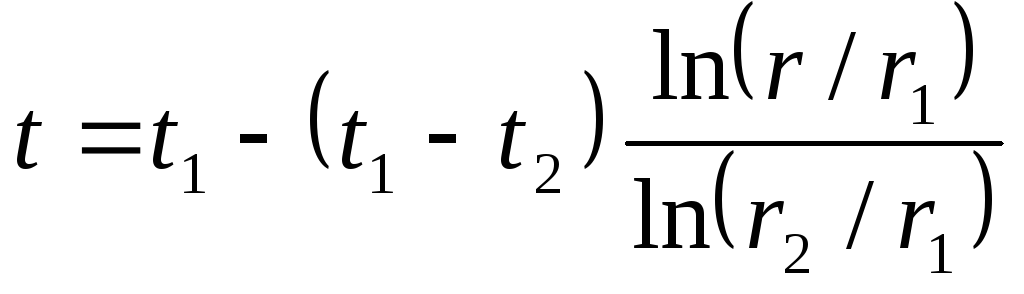
или

. (4.31)

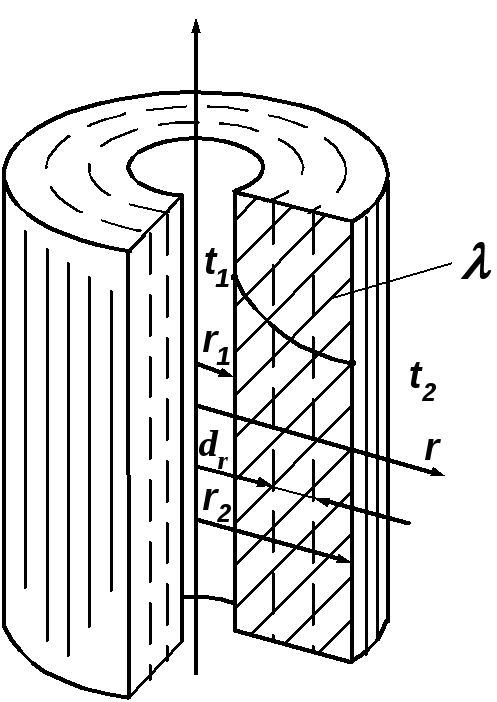
Рис. 4.5. Температурное поле однослойной цилиндрической стенки

Уравнение (4.31) представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки плотность теплового потока остается одинаковой для всех изотермических поверхностей и градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность изменяется, т. к. величина поверхности зависит от радиуса (H=2rl), что приводит к изменению градиента температуры.

Для нахождения количества теплоты, проходящего через цилиндрическую поверхность величиной Н в единицу времени, можно воспользоваться законом Фурье

.

Подставляя значение градиента температуры и поверхности, получаем

, Вт. (4.32)

Из уравнения (4.32) следует, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, полностью определяется заданными граничными условиями.

Тепловой поток (4.32) может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности.

Расчетная формула для плотности теплового потока, проходящего через единицу длины трубы, запишется:

, Вт/м. (4.33)

Тепловой поток, отнесенный к единице трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (4.33), при неизменном отношении d₂/d линейная плотность теплового потока не зависит от поверхности цилиндрической стенки.

Тепловой поток через единицу внутренней поверхности запишется:

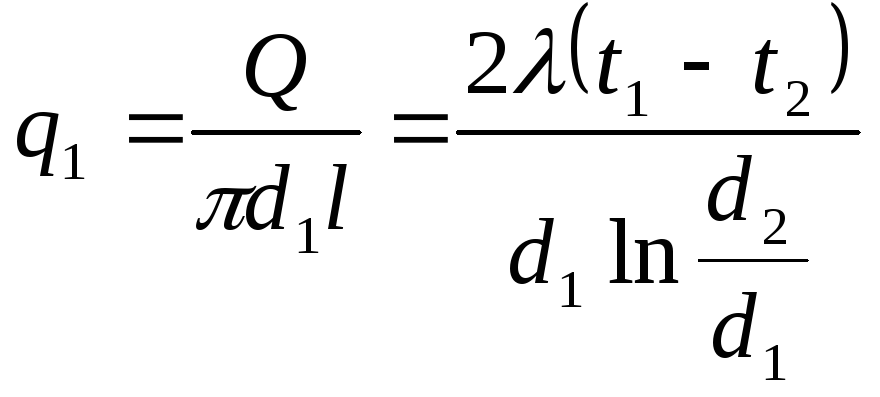, Вт/м. (4.34)

Тепловой поток через единицу наружной поверхности запишется:

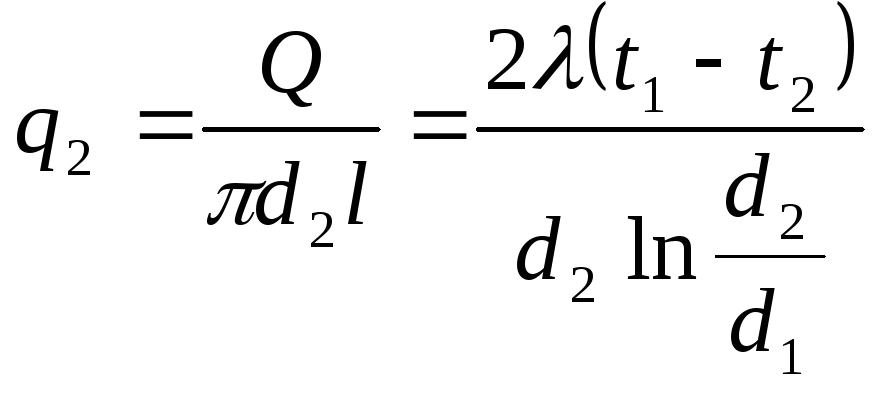, Вт/м. (4.35)

На основании полученного уравнения теплового потока на единицу длины трубы (4.33) можно получить уравнение теплового потока многослойной цилиндрической стенки. В этом случае необходимо выразить разности температур слоев из указанного уравнения, а затем, аналогично примеру с плоской стенкой, сложить полученные результаты. В результате получаем уравнение теплового потока многослойной цилиндрической стенки:

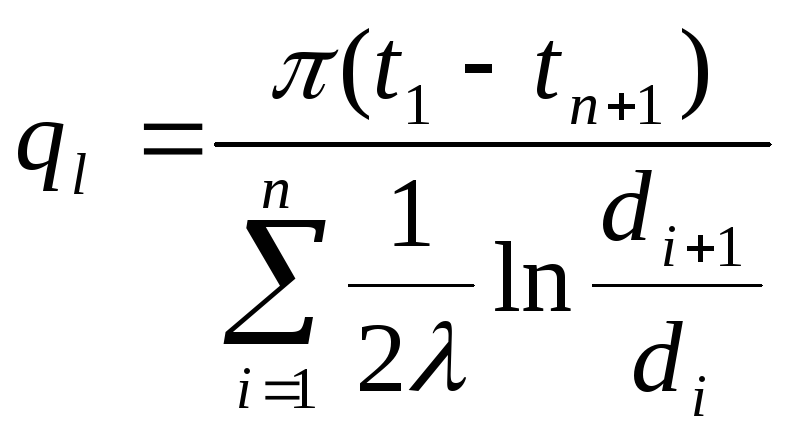, Вт/м. (4.36)

Величина, стоящая в знаменателе, называется полным термическим сопротивлением многослойной цилиндрической стенки. Уравнение (4.36) может быть использовано для определения температур на границах любого слоя:

. (4.37)

Таким образом, полученные уравнения температурного поля и теплового потока позволяют определить температуры в любой требуемой точке тела (пластины или цилиндра) и определить величину теплового потока.

Температурное поле для шаровой стенки имеет вид

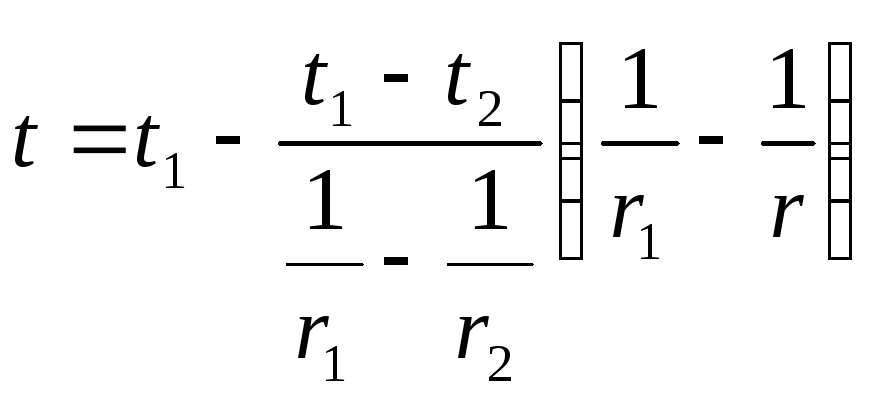. (4.38)

Тепловой поток определяется по уравнению

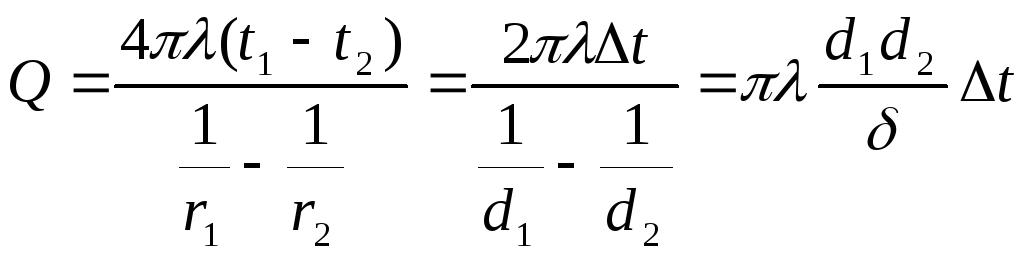, Вт. (4.39)

Указанные уравнения можно использовать для расчета температур в агрегатах и узлах автомобиля. Например, распределение температур по толщине двигателя или стенки кабины можно считать по уравнениям плоских стенок; карданных валов — по уравнениям цилиндрических стенок; заднего моста, главной передачи — по уравнениям шаровых стенок.