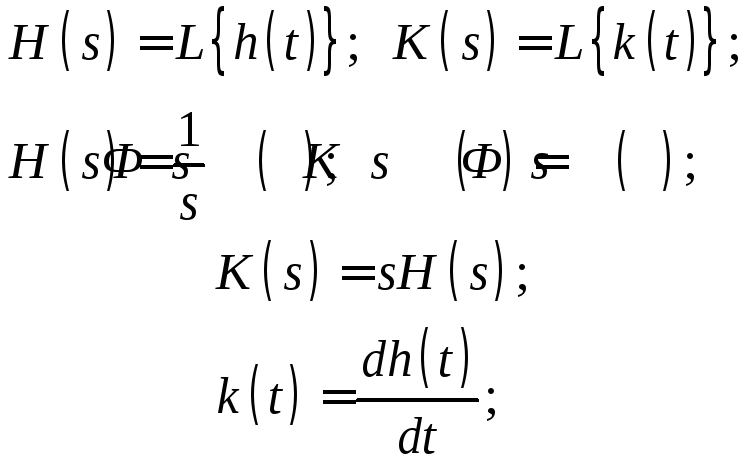13. Временные и частотные хар-ки дифференцирующего звена второго порядка.

Мат. модели:

Временные характеристики:

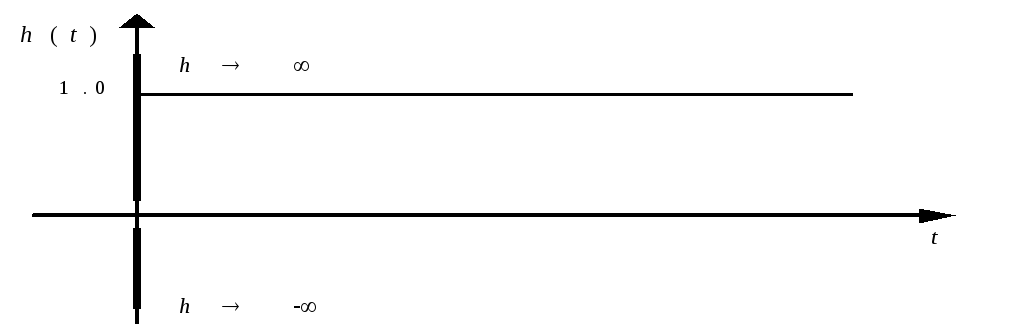
Частотные характеристики:

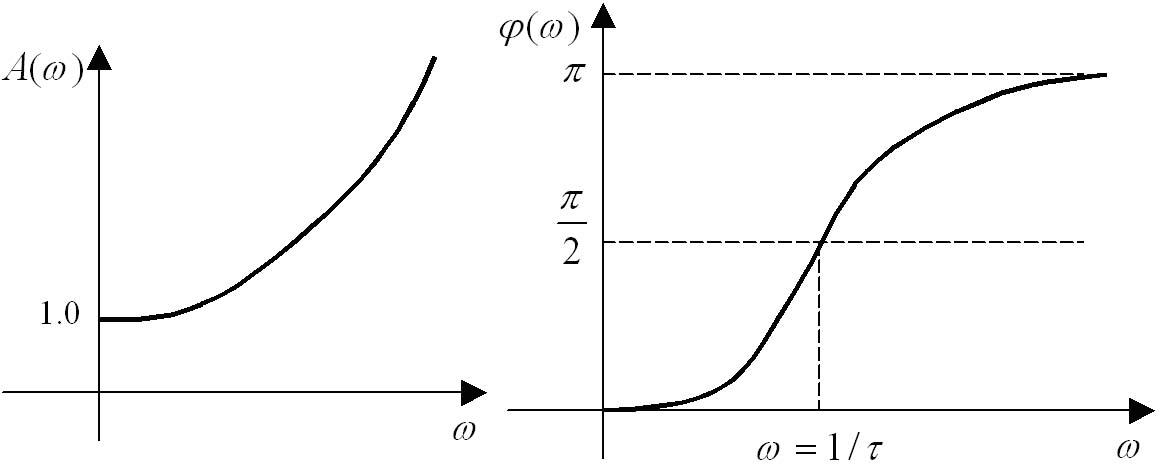
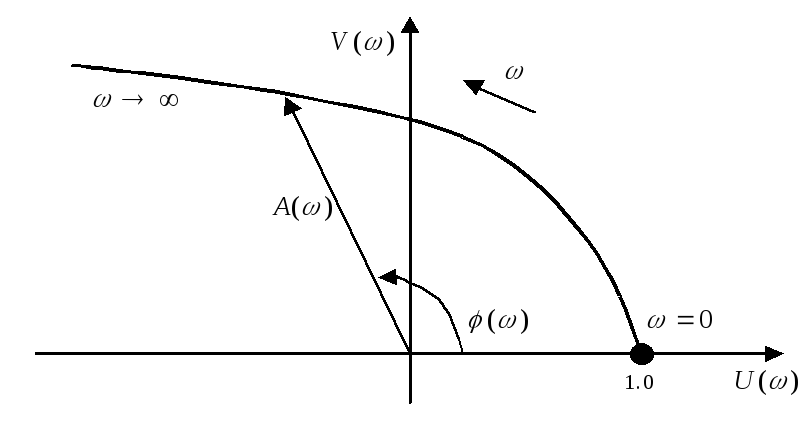
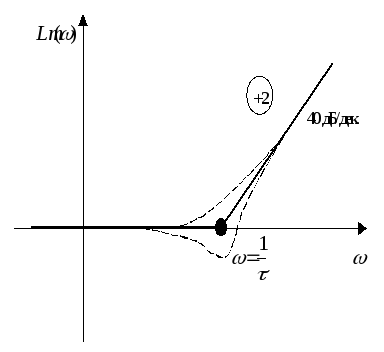
14. Понятие о неминимально фазовых звеньях сау:

Звено называется минимально фазовым, если все нули и полюсы его передаточной функции имеют отрицательные или равные нулю вещественные части.

Звено называется неминимально фазовым, если хотя бы один нуль ил полюс его передаточной функции имеет положительную вещественную часть.

Примером НМФЗ могут служить звенья: апериодическое, колебательное, ДЗПП.

Для НМФЗ характерно то, что у него сдвиг фазы по модулю больше, чем у МФЗ, имеющую одинаковую с неминимально фазовым звеном АЧХ.

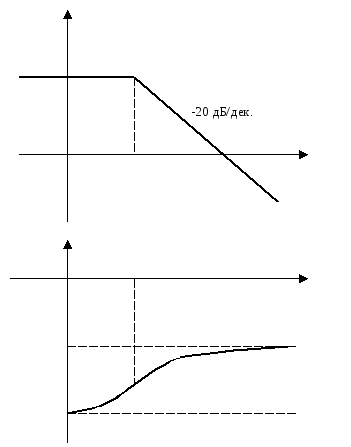
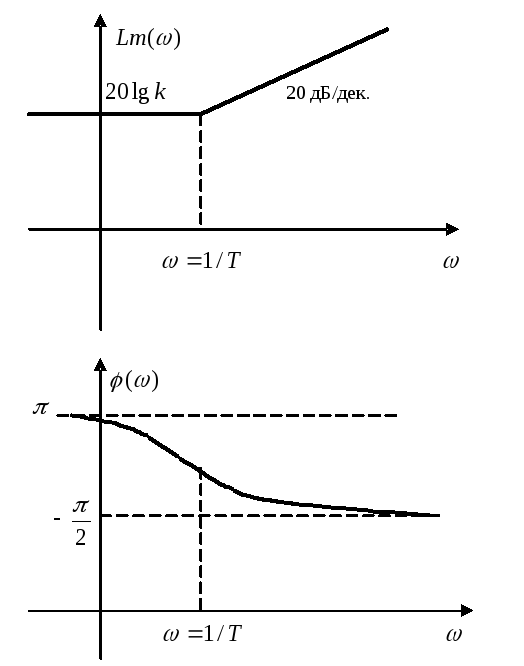
15. Лачх разомкнутых сау

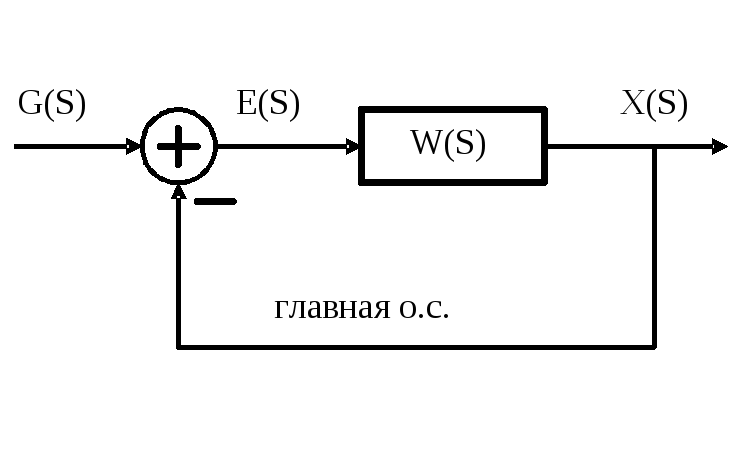
Расчетная схема:

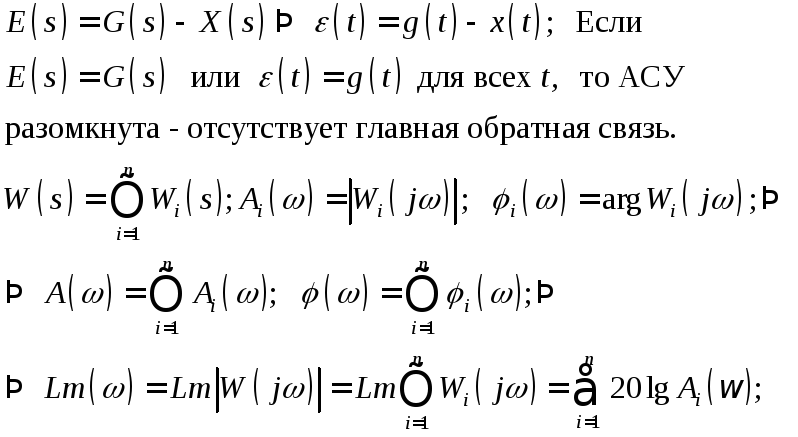
Т.о. для построения ЛАЧХ разомкнутой САУ нужно:

1. Передаточную ф-ию разомкнутой САУ представить произведением элементарных звеньев.

2. Построить ЛАЧХ элем. звеньев сис-мы, и затем суммировать.

Замечание: При построении асимптотической ЛАЧХ элементарных звеньев при частотах меньше сопрягающей частоты, под корнем оставляют только единицу, а остальными членами пренебрегают. При частотах, больше сопрягающей частоты, оставляют члены с наивысшей степенью ω.

Общее правило построения асимптотической ЛАЧХ:

1. Получить передаточную функцию разомкнутой САУ:

2. Представить эту передаточную ф-ию в виде:

3. Определить сопрягающие частоты и значение 20lgk.

4. Через точку {1, 20lgk} провести первую асимптоту с наклоном –ν до первой сопрягающей частоты.

5. Провести вторую асимптоту от правого края первой до второй сопр. частоты. Ее наклон изменится в зависимости от типа звена.

6. Повторять пункт 5 пока не надоест.

Если какая-либо сопрягающая частота является кратной и ее кратность равна μ (т.е. имеется μ одинаковых звеньев), то изменение наклона при этой частоте в μ раз больше.

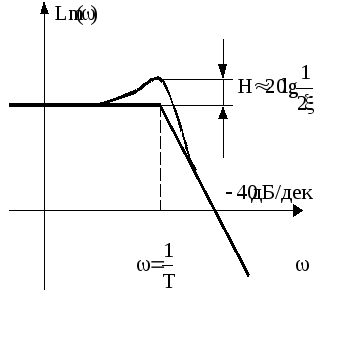
Для колебательных звеньев необходимо выполнить поправки в соответствии с графиками, шаблонами и т.п. или по формуле:

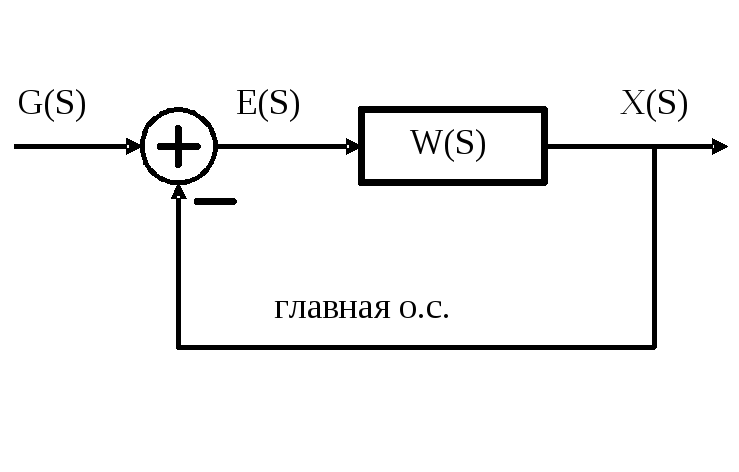
16. Характеристики замкнутых сау:

Расчетная схема:

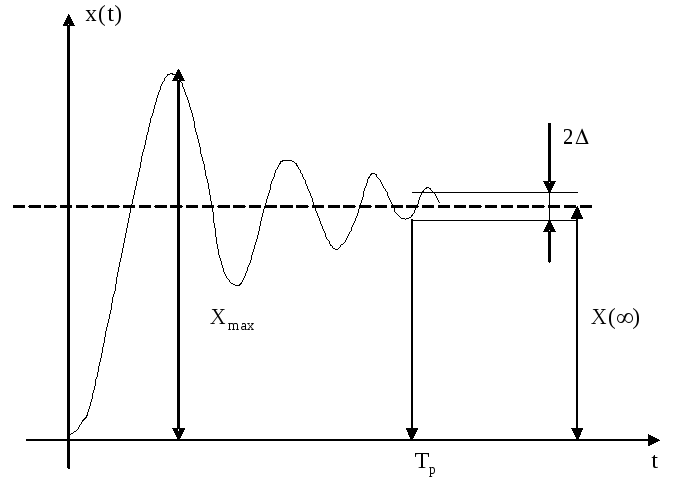
Временные хар-ки ЗСАУ:

Переходная ф-ия ЗСАУ – это ее реакция на единичное вход. возд.

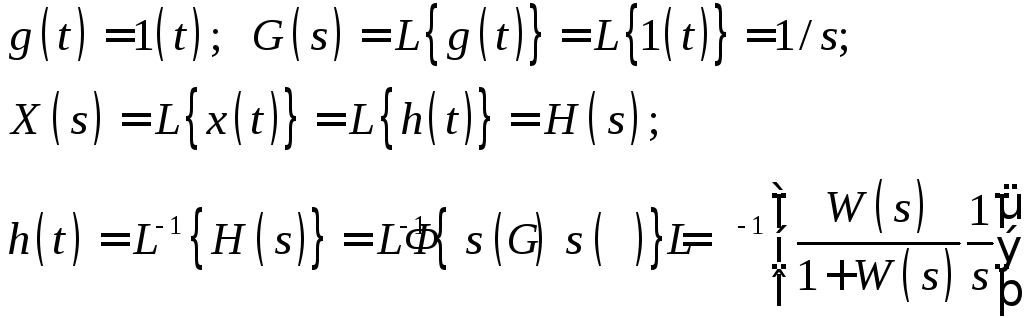
Можно определить установившееся значение переходной ф-ии, если воспользоваться предельными теоремами Лапласа. Имеем:

Для ошибки системы справедливы следующие равенства:

Можно определить установившееся значение ошибки системы, если воспользоваться предельными теоремами Лапласа. Имеем:

Импульсная переходная (весовая) ф-ия замкнутой сис-мы:

Весовая функция – ф-ия, описывающая реакцию система на входное δ-воздействие при начальных нулевых условиях.

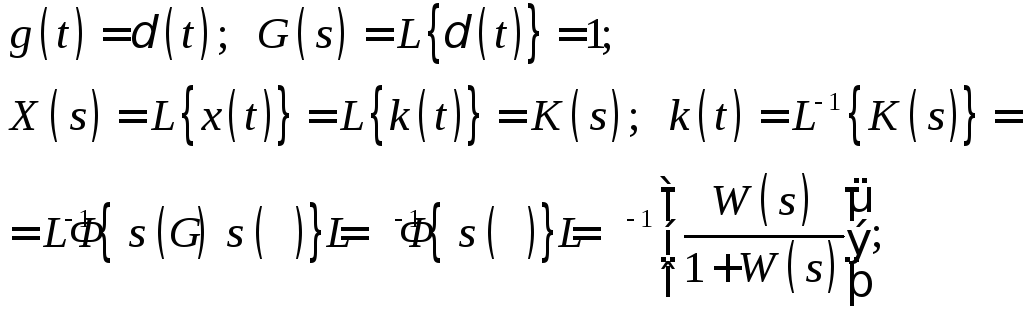
Можно определить установившееся значение весовой ф-ии системы, если воспользоваться предельными теоремами Лапласа:

Связь между импульсной переходной (весовой) ф-ией и переходной ф-ией: