20. Устойчивость линейных сау, необходимое и достаточное условие устойчивости, необходимое условие устойчивости.

22. Алгебраический критерий устойчивости Гурвица.

L(s) и M(s) – полиномы степени m и n, причем m<n.

Хар. полином:

Для того чтобы исследовать устойчивость замкнутой системы нужно составить матрицу G размера nxn из коэф-тов хар. полинома по правилу:

1. По главной диагонали выписываем коэф-ты хар. полинома, начиная с a₁ до a_n.

2. Каждый столбец матрицы G вверх от диагонального элемента заполняется по возрастающим индексам.

3. Каждый столбец ниже диагонального элемента заполняется коэф-тами по убывающим индексам.

4. Все эл-ты матрицы G выше a_n и ниже a₀ заполняются нулями.

После составления матрицы Гурвица по ней можно судить об устойчивости замкнутой САУ.

Обозначим через Δ₁,…, Δ_n диагональные миноры матрицы G.

Для того чтобы замкнутая САУ была устойчива, необходимо и достаточно чтобы Δ₁ > 0, Δ₂ > 0,…, Δ_n = det(G) > 0.

С помощью критерия Гурвица можно найти область изменения значений параметров системы, при которых она будет обладать св-вом устойчивости. Для этого: Δ_n = det(G) = 0. В результате получим уравнения границ устойчивости: a_n = 0, Δ_n-1 =0. Первое уравнение соответствует наличию у хар. полинома ЗСАУ нулевого корня λ=0. 2ое Ур-е соответствует наличию у хар. полинома системы пары чисто мнимых корней λ = ±jω.

Эти ур-я разбивают пр-во параметров ЗСАУ на области, в кот. все остальные Δ_k > 0 соответствуют значениям коэф-тов хар. полинома, при кот. ЗСАУ будет асимптотически устойчива. Вне этих областей значений параметров, система неустойчива.

19. Определение устойчивости по Ляпунову.

Пусть мат. моделью САУ явл. сис-ма нелин. дифуров n-ого порядка, которая записана в нормальной форме Коши:

Пусть внеш. возмущ. отсутствуют и что в нач. мом-т вр. нач. полож. сис-мы известно: . Тогда начальными условиям последнего равенства соответствует единственное реш. сис-мы дифуров:Это решение можно рассматривать, как ур-е некот. траект.в пр-ве переменных состояния. Эта траект. подлежит исследов. на устойчивость. Всякую траекторию движения САУ, кот. исследуется на устойч., будем назыв.невозмущ. движ-ем сис-мы и обозначать: .

Выбор невозмущ. движ-я произвольный, это может быть любое возмож. движ-е сис-мы, как установившееся, так и нет. Н.у:

Пусть заданы небольшие по модулю числа ε₁, …, ε_n. Рассмотрим движение сис-мы ур-й (*) при н.у.: .

Движение сис-мы, отвечающее измененным н.у. будем называть возмущенным движением, y_i(t). Т.е. возмущенным движением сис-мы называют всякое иное движение, которое отличается от невозмущенного. Введем отклонения:

Если все отклонения равны нулю, то возмущенное движ-е совпадает с невозмущенным. Запишем уравнения возмущенного движ-я в отклонениях: А невозмущенное движение будет:Переменныеявл. координатами состояния системы (**).

П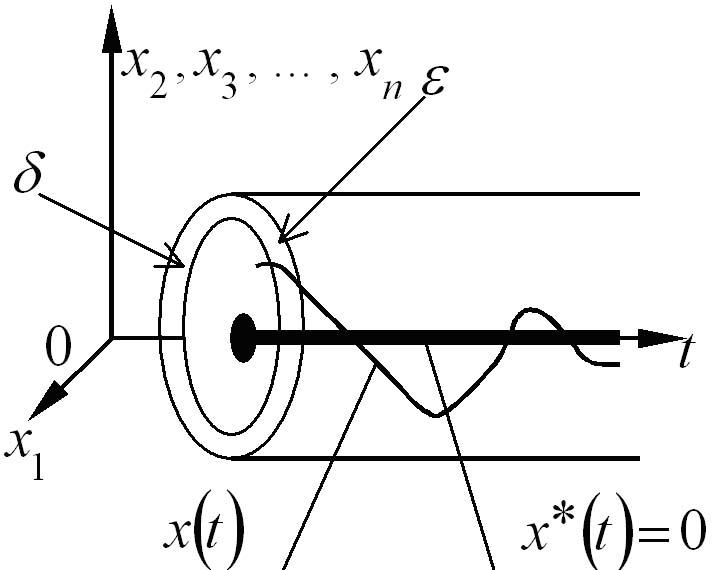усть приt = t₀ переменные x_i принемают какие-либо свои нач. знач. x_i0, из которых, по хотя бы одно не равно нулю: . Эти начальные отклонения будем называтьвозмущениями. Геометрически это можно изобразить следующим образом:

О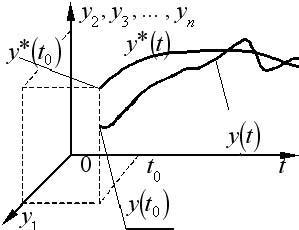ПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ:

Невозмущенное движение системы называется устойчивым, если при заданномε > 0, сколь бы оно мало ни було, существует такое δ > 0, зависящее от ε, что при начальных условиях , в дальнейшем движении (t₀ < t < ∞) будет все время .

Иными словами, невозмущенное движение системы называется устойчивым, если, задав «трубку» сколь угодно малогоn-мерного сечения ε, можно подобрать в начальный мом-т времени t₀ такую область начальных условий δ, зависящую от ε, что в дальнейшем с увеличением t возмущенное движение не выйдет из заданной трубкиε.

Невозмущенное движение будет неустойчивым, если это условие не выполняется хотя бы для одного.

Если имеем , то невозмущенное движениеназывается асимптотически устойчивым.

Если рассмотреть фазовую траекторию, то она будет такой:

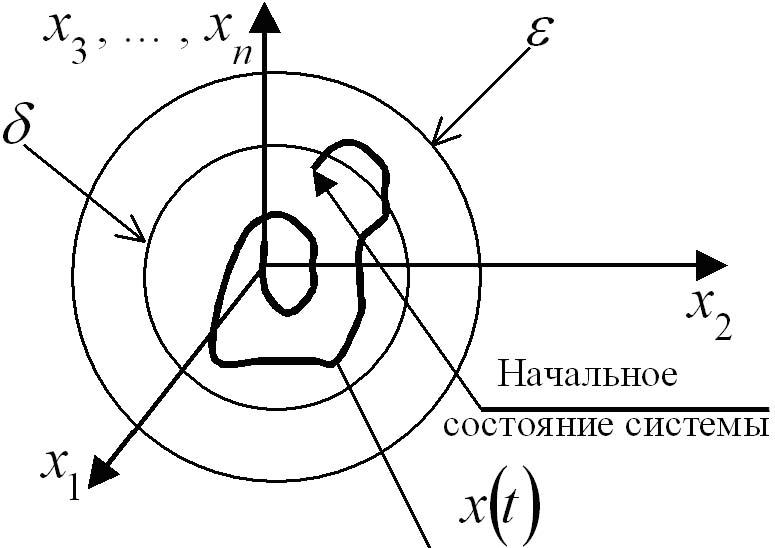
Особенности:

- Предполагается, что возмущения налагаются только на начальные условия. Т.е. возмущенное движение происходит при тех же силах, что и невозмущенное.

- Устойчивость рассматривают на бесконечно большом промежутке времени.

- Возмущения предполагаются малыми.