Оптимизационная задача управления запасами

Метод и модель Задачей управления запасами называется оптимизационная задача, в которой предполагаются известными данные о поставках товара на склад, спросе на товар, издержках и условиях хранения товарных запасов. Требуется оптимизировать работу склада по заданному критерию оптимизации [35].

Классическая задача управления запасами состоит в следующем. Выберем за единичный интервал времени один день. Пусть к концу дня t - 1 на складе находится запас в объеме х_t-1 ≥ 0. Склад делает заказ на пополнение запаса товара в объеме h_t. Это пополнение поступает к началу следующего дня t, так что запас товара в начале следующего дня составляет х₁ + h_t. Пусть S_t — объем товара, запрашиваемый потребителем (или потребителями) в день t (объем заявки).

Если S_t ≤ х_t-1 + h_t, то склад удовлетворяет заявку потребителя полностью, а остатки товара (х_t = х_t-1 + h_t — S_t) переносятся на следующий день (t + 1), причем издержки хранения этого запаса пропорциональны его объему, т.е. с*х_t = с*(х_t-1+h_t – S_t).

Если объем заявки S_t > х_t-1 + h_t„то склад полностью отдает свой запас, а за недопоставленный товар несет потери (например, штрафуется за дефицит), пропорциональные объему дефицита, т.е. k*(S_t – х_t-1 - h_t) = - k*(x_t-1 + h_t - S_t).

Таким образом, полные издержки φ(х_t-1, h_t, S_t) склада можно записать в виде:

φ(х_t-1, h_t, S_t) = max {с(х_t-1 + h_t — S_t); — k(x_t-1 + h_t - S_t)}. (5.1)

При этом остаток товара такой

Х_t = max {0; х_t-1 + h_t - S_t }.

Из уравнения (5.1) следует: если х_t-1 › 0, то φ(х_t) = с*х_t; если х_t <0, то φ(х_t) = - k*х_t; если х_t = 0, то φ(х_t) = 0.

В классической постановке задачи управления запасами предполагается, что сама величина спроса S, неизвестна, однако она является независимой случайной величиной, имеющей заданный закон распределения. Пусть распределение вероятностей величины S_t задается непрерывной функцией распределения F(x) с плотностью распределения f(х). Тогда средние полные издержки Ф (х_t-1 + h_t) задаются следующей формулой:

Ф(х_t-1+h_t)= Мφ(х_t-1, h_t, S_t) = ,

где М — математическое ожидание.

Задача ставится таким образом: определить объем заказа на пополнение h_t , минимизирующий средние полные издержки, т.е.:

Ф(x_t-1 + h_t) → min,

где h_t ≥ 0.

Если обозначить у = x_t-1 + h_t, то в случае статической постановки классической задачи управления запасами уравнение для определения минимизирующего запаса у* имеет вид:

(5.3)

Решение (5.3) задачи (5.2) определяет стратегию оптимального пополнения запасов. Величина пополнения запасов h_t^*, минимизирующая средние полные издержки, задается следующим образом:

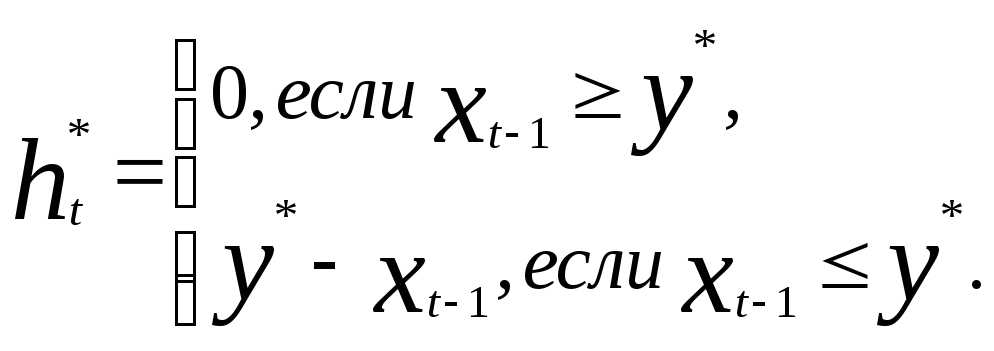
Конкретные числовые характеристики системы управления запасами зависят от вида функции плотности распределения f(х) случайной величины спроса. В качестве примера рассмотрим случай симметричного «треугольного распределения» спроса, при котором функция плотности распределения получается в виде графика. График получается при параллельном переносе вправо (т.е. заменой х на х + а) графика.

При этом функция принимает следующий вид: