4 Аналіз множинної кореляції

4.1 Теоретичні основи множинного лінійного кореляційного аналізу

Більш актуальним на практиці є здійснення аналізу не простих кореляції, а множинних. Адже економічні явища склада­ються під впливом не одного, а багатьох різних факторів, кож­ний з яких окремо може не справляти вирішального впливу. Спільний же вплив факторів іноді виявляється досить сильним, щоб за їх змінами можна було робити висновки про величину показника досліджуваного явища.

У моделях множинної кореляції залежна зміна у розгля­дається як функція кількох (в загальному випадку) незалежних змінних х.

Припущення про існування лінійного рівняння множинної регресії може бути представлене в такому вигляді:

Із погляду геометрії це рівняння визначає в просторі пло­щини відповідних змінних та у.

Параметри наведеного рівняння знаходять, розв'­язавши систему нормальних рівнянь:

Множинне кореляційне рівняння встановлює зв'язок між досліджуваними ознаками і дає змогу вирахувати очікувані зна­чення результативної ознаки під дією включених в аналіз ознак -факторів, пов'язаних із даним рівнянням. У вузькому розумінні рішення кореляційних моделей охоплює операції по знаходжен­ню числових значень параметрів досліджуваних залежностей.

При вивченні множинного кореляційного зв'язку результа­тивної ознаки, наприклад, із двома факторними аналітичне рів­няння регресії має вигляд: .

Параметри a₀, a₁ і a₂ розраховують розв»язуючи систему нор­мальних рівнянь:

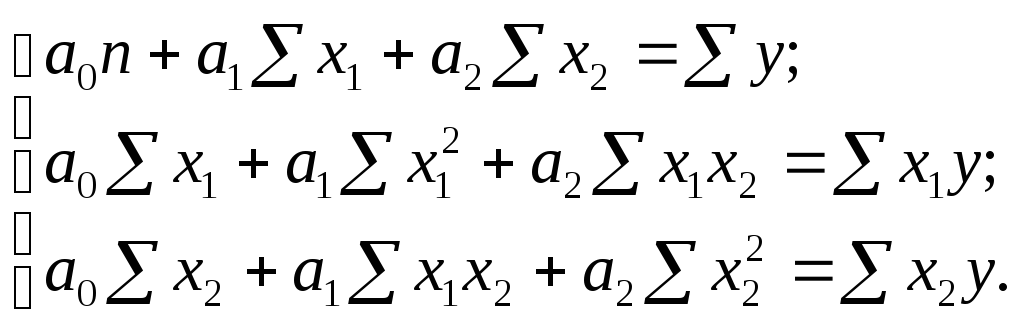
Для оцінки тісноти зв”язків у множинних лінійних кореляційних моделях застосовують три види коефіцієнтів кореляції: 1) прості коефіцієнти кореляції 2) частинні коефіцієнти кореляції 3) множинні коефіцієнти кореляції.

У множинних кореляційних моделях коефіцієнти простої кореляції між результативною ознакою і факторними, а також між самими факторними ознаками розраховують за вже відомими формулами (для двофакторної моделі буде три простих коефіцієнти кореляції):

; ; .

Оскільки існує залежність між факторами, які включені до множинної моделі, то простий коефіцієнт кореляції не може характеризувати «чистого» впливу даного фактора на результативну ознаку.В простому коефіцієнті кореляції крім «чистого» впливу даного фактора є також певна частина опосередкованого впливу інших факторів.

Для оцінки частинної (чистої) кореляції між двома досліджуваними ознаками, обчислюють частинні коефіцієнти кореляції. Отже, при досліджен­ні впливу двох факторних ознак частковий коефіцієнт кореляції характеризує тісноту лінійного зв'язку результативної ознаки (у) з однією із факторних ознак (х₁) при виключенні дії іншої факторної ознаки (х₂) і навпаки, вплив ознаки х₂ при виключен­ні впливу ознаки х₁.

Формули для визначення значень величин частинних коефі­цієнтів кореляції мають вигляд:

; .

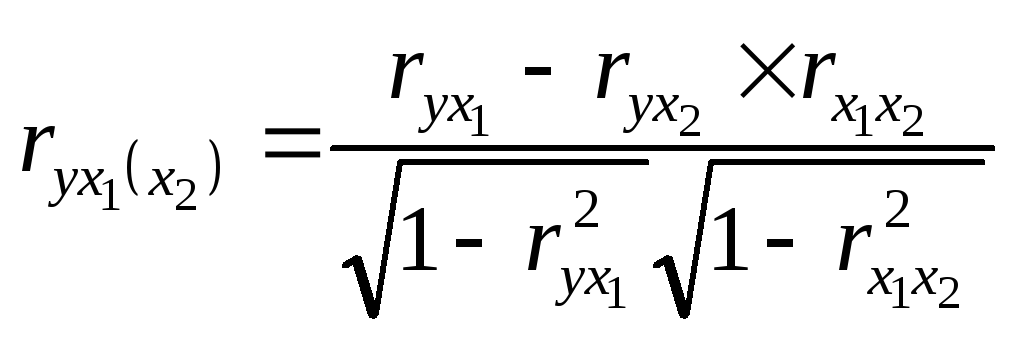Перша з наведених формул характеризує ступінь тісноти зв'язку результативної ознаки із факторною х₁ при виключенні впливу фактора х₂, друга  аналогічну залежність при виклю­ченні впливу фактора х₁.

Величина частинного коефіцієнта кореляції подібно до простого коефіцієнта може мати до­датнє і від'ємне значення, тобто вказувати на прямий чи обер­нений зв'язок між досліджуваними ознаками, а за модулем знаходиться між "0"і "1".

Використання в аналізі частинної кореляції дає змогу поглибити кількісне вивчення досліджуваних зв'язків між со­ціально-економічними процесами і явищами, виявляючи вплив конкретних причин варіації результативної ознаки.

Для оцінки ступеня впливу тісноти звя'зку між результа­тивною і сукупністю кількох факторних ознак обчислюють коефіці­єнт множинної (сукупної) кореляції.

Коефіцієнт множинної кореляції характеризує інтен­сивність кореляції (або ступінь тісноти зв'язку) між залежною змінною та кількома незалежними змінними. Його величина не може бути меншою, ніж абсолютна величина будь-якого коефі­цієнта простої чи частинної кореляції. Множинний коефіцієнт кореляції завжди має додатний знак і змінюється від 0 до 1.

Загальний математичний вираз коефіцієнта множинної ко­реляції має вигляд:

,

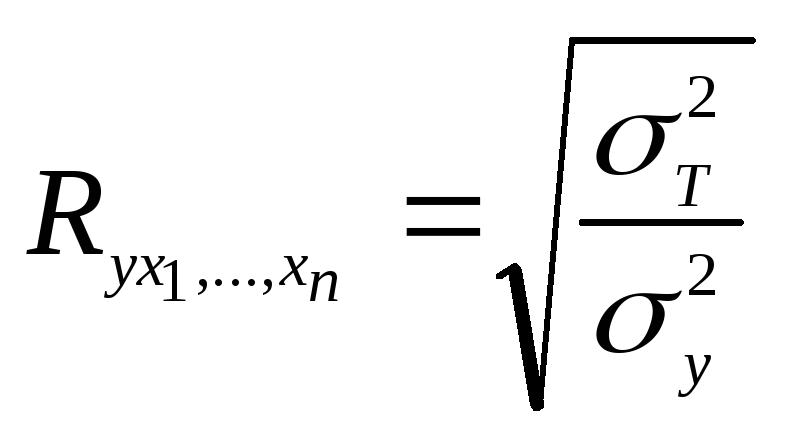де  факторна (відтворена) дисперсія;  загальна дисперсія.

Існуюють й інші формули множинного коефіцієнта кореляції.

Коефіцієнт множинної кореляції можна обчислити за зна­ченнями величин коефіцієнтів простої кореляції. Так, для дво­факторної моделі величину його розраховують за формулою:

.

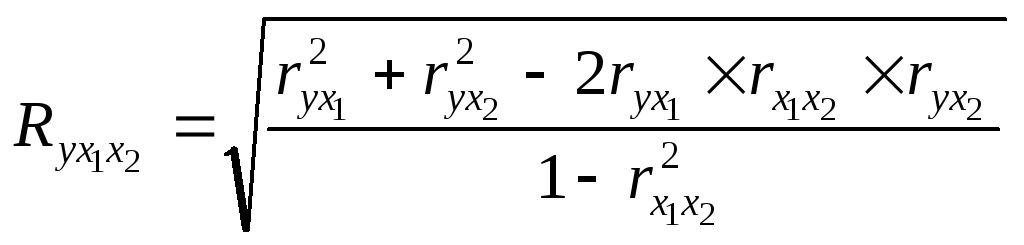В кореляційному аналізі можна визначити не тільки ступінь тісноти у вигляді коефіцієнтів кореляції чи індексів кореляції, а й встановити, на скільки процентів варіація результативної ознаки обумовлена впливом кожного фактора зокреми або усіх факторів разом взятих.Для цього обчислюють коефіцієнти детермінації.

Для простої кореляції коефіцієнт детермінації визначається як квадрат простого коефіцієнта кореляції (індекса кореляції): d = r²*100.

Аналогічно визначається множинний коефіцієнт детермінації : D = R²*100.

Частинний коефіцієнт детермінації (наприклад, для фактора х₁) визначають за формулою: d₁ = r_ух1* a₁*(σ_x1 :σ_у)*100.

Коефіцієнти детермінації мають додатні значення.Сума частинних коефіцієнтів детермінації для даної кореляційної моделі завжди дорівнює множинному коефіцієнту детерміннації.