§ 2.6. Каноническое распределение в классическом приближении. Распределение Максвелла и Больцмана

Чтобы определить состояний системы при квантовом рассмотрении, необходимо знать все квантовые числа всех частиц системы, то есть квантовые состоянии всех частиц системы, которые и определяют состояния n системы и ее энергию E_n. При этом вероятность такого состояния будет

P_n(E_n) = e^-En/kT/z

В классическом приближении состояния каждой частицы системы определяются координатами R и импульсом P. Чтобы определить состояние всей системы, нужно знать координаты и импульсы всех частиц системы. Полная энергия системы при этом будет зависеть от координат и импульсов всех ее частиц.

E = E(p,q)

Определим вероятность того, что координаты первой частицы лежат в интервале от R₁ до R₁ + dR₁, а ее импульс при этом - в интервале от p₁ до p₁ + dp₁, при этом координаты второй частицы – в интервале от R₂ до R₂ + dR₂, а ее импульс при этом - в интервале от p₂ до p₂ + dp₂ и так далее для всех частиц.

Чтобы вычислить такую вероятность, надо определить, каким квантовым состоянием системы n соответствует рассматриваемый интервал, вычислить вероятность каждого такого состояния и затем сложить. Если рассматриваемые интервалы dp и dq бесконечно малы, то в классическом приближении энергия будет одинакова и будет

P_n(E) = e^-E(p,q)/kT/z

Чтобы вычислить рассматриваемую вероятность, надо взять вероятность одного состояний и умножить на число состояний, при которых частицы системы лежат в интервалах dp и dq.

Чтобы определить число таких состояний, рассмотрим сначала одну частицу в одномерном случае и найдем число состояний, при которых ее координата лежит в интервале от x до x + dx, а проекции импульса - в интервале от p до p + dp.

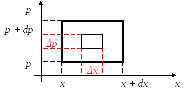
Из квантовой механики известно, что для каждой частицы в этом случае выполняется принцип неопределенности Гайзенберга

ΔpΔx ≈ 2ħΠ

Таким образом, число состояний, при которых импульс и координаты частиц лежат в заданных интервалах будет dpdx/2ħΠ; если ситема состоит из “n” частиц dpdq/(2ħΠ)^3N. И тогда вероятность будет

W(p,q)dpdq = (e^-E(p,q)/kT/z)(dpdq/(2ħΠ)^3N) = c₀ e^-E(p,q)/kTdpdq

Постоянный коэффициент c₀ можно определить из условия нормировки

∫W(p,q)dpdq = 1 = c₀ ∫ e^-E/kTdpdq

Определим вероятность того, что импульс первой частицы лежит в интервале от P₁ до P₁ + dP₁, а импульс второй частицы - от P₂ до P₂ + dP₂ и так далее для импульсов всех частиц при любых значениях их координат.

Чтобы найти эту вероятность, надо полную вероятность просуммировать по всем возможным координатам всех частиц. Тогда

W(p)dp= dp ∫W(p,q)

Полная энергия системы в классическом приближении состоит из кинетической и потенциальной

E(p,q) = T(p) + u(q)

W(p,q)dpdq = dp ∫c₀ e^-E/kTdq = dp ∫c₀ e^-T(p)/kT e^-u(q)/kT dq = dpc₀ e^-T(p)/kT∫e^-u(q)/kT dq = c₁ e^-T(p)/kTdp

Постоянный коэффициент c₁ можно легко определить из условия нормировки. Определим вероятность того, что импульс первой частицы леит в интервале от P₁ до P₁ + dP₁. При любых значениях импульса всех остальных частиц

W₁(p₁)dp₁ = dp₁∫W(p)dp₂ dp₃ dp_n

Кинетическая энергия системы будет

T(p) = (dp₁²/2m) + ∑(dp_i²/2m)

Тогда

W₁(p₁)dp₁ = [c₂ e ^(-p₁²/2mkT)]dp₁

W₁(p₁) = [c₂ e ^(-p₁²/2mkT)] – распределение Максвелла

Определим вероятность того, что координаты первой частицы лежат в интервале от R₁ до R₁ + dR₁, второй частицы – в интервале от R₂ до R₂ + dR₂ и так далее для всех частиц при любых значениях их импульсов.

W(q)dq = dq ∫W(p,q)dp = dqc₀e^-u(p)/kt ∫ e^-T(p)/kt dp = c₃e^-u(q)/ktdq

Определим вероятность того, что координаты первой частицы лежат в интервале от R до R + dR при любых координатах всех остальных частиц. Потенциальная энергия идеального газа равно сумме потенциальных энергий всех частиц системы. При этом потенциальная энергия каждой частицы зависит только от координат.

u(q) = u₁(R₁) + ∑u_i

W₁(R₁)dR₁ = dR₁ ∫c₃e^-u(q)/ktdR₂dR₃…= c₄ e^-u(R1)/ktdR₁ – распределение Больцмана

Среднее число частиц f(p)dp, импульс которых лежит в интервале от P до P + dP , будет

f(p)dp = NW₁(p)dp

W₁(p) – плотность вероятности