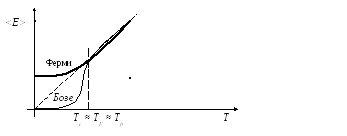§ 2.9. Теорема о равномерном распределении. Многоатомный идеальный газ

Рассмотрим идеальный газ, молекула которого состоит из “n” атомов. Тогда общая энергия газа будет E = ∑E_i

Энергия одной молекулы будет

E_i = E_k + E_n

E_k – кинетическая энергия молекулы

E_n – потенциальная энергия молекулы

Потенциальная энергия определяется энергией взаимодействия атомов в молекуле. Определим вклад в общую энергию системы от одной степени свободы в системе. На одну степень свободы в кинетической энергии системы приходится mV_x²/2 энергии, где m – масса атома. Тогда средний вклад будет

<mV_x²/2> = m< V_x²>/2 = mkT/2m = kT/2

То есть на одну степень свободы приходится kT/2 кинетической энергии. Рассмотрим вклад в потенциальную энергию системы, приходящуюся на одну степень свободы. Будем считать, что потенциальная энергия атомов в молекуле является квадратичной функцией координат. Тогда вклад в потенциальную энергию от одной степени свободу будет b₁x².

<b₁x²> = b₁<x²>

<x²> = ∫ x²W₁(x)dx

W₁(x) – плотность вероятности, определяется распределением Больцмана

W₁(x) = c₇e^(-b₁x²/kT)

Постоянный коэффициент можно найти из условия нормировки

c₇ = (b₁/ПkT)^1/2

<x²> = (b₁/ПkT)^1/2 ∫ x²e^(-b₁x²/kT)dx = kT/2b₁

Тогда средний вклад в потенциальную энергию на одну степень свободы будет

<b₁x²> = kT/2

Теорема о равномерном распределении: на каждую степень свободы потенциальной и кинетической энергии системы приходится вклад kT/2.

Рассмотрим зависимость полной средней энергии системы от температуры. При достаточно низких температурах вращательные и колебательные степени свободы молекул не возбуждаются. Поэтому при низких температурах молекула газа обладает лишь тремя степенями свободы, определяющими движение ее центра масс. Средняя энергия одной молекулы будет 3kT/2, то есть три степени свободы вносят вклад в кинетическую и потенциальную энергии 2NkT/2.

При увеличении температуры возбуждаются вращательные степени свободы, которые тоже вносят вклад в кинетическую энергию. Вращательных степеней свободы у всех молекул три, кроме линейных и двухатомных. Тогда вклад в кинетическую энергию от вращательной степени свободы будет 3NkT.

Оставшиеся степени свободы приходятся на колебательное движение. Каждой колебательной степени свободы соответствует kT/2 кинетической и колебательной энергии.

§ 2.10. Условие применимости классического приближения и вырождения идеального газа

Как известно, среднее число частиц, энергия которых лежит в интервале от E до E + dE, определяется квантовым распределением.

f(E)dE = c₀V(E)^1/2dE/( e^{(E - μ)/kT} ± 1)

“+” – распределение Ферми

“-” – распределение Бозе

V – объем системы

c₀ – можно найти из условия нормировки

∫f(E)dE = N

Это распределение справедливо всегда. В классическом приближении среднее число частиц, скорость которых в интервале от V до V + dV, дается распределением Максвелла.

f(V)dV = 4NП(m/2ПkT)^3/2V²e^(-mV²/2kT)dV

Для идеального газа E = mV²/2

dE = mVdV

f(E)dE = c_o1N(E)^1/2e^-E/kTdE

Сравнивая полученные распределения, заметим, что классическое приближении будет совпадать с квантовым, если e^(E-μ)/kT>>1. Тогда

f(E)dE = c_oV(E)^1/2e^μ/kT e^-E/kT dE

Таким образом, условием применимости классического приближения будет e^E-μ/kT>>1. Это условие должно выполняться для любых значений энергии, в том числе и в самой трудном случае (E = 0). То есть e^-μ/kT>>1.

Рассмотрим классическое приближение

N = ∫ f(E)dE = c_oVe^μ/kT ∫(E)^1/2 e^-E/kT dE = c_o2Ve^μ/kT(kT)^3/2 = N

e^-μ/kT = c_o2V(kT)^3/2/N >>1

T>>(N/c_o2V)^2/3(1/k)

Если Т_сист. > Т _{с(критич)}, где Т_сист = (N/c_o2V)^2/3(1/k), то можно пользоваться классическим приближением. Заметим, что критическая температура определяется концентрацией частиц системы N/V.

Вырожденная система – система, основная часть частиц которой находится в состоянии с минимальной энергией.

Рассмотрим ферми-частицы, функция распределения которых имеет вид

f(E)dE = c_oV(E)^1/2 dE/ (e^(E-μ)/kT + 1)

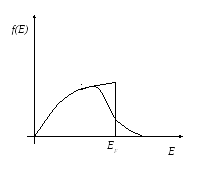
Ферми-газ считается вырожденным, если частиц с энергией E большей, чем E_F, будет мало.

Это условие будет выполняться, если

e^(E-μ)/kT > 1 E > E_F

Наилучший случай, когда μ максимально большое.

e^(E-Ef)/kT >> 1 E > E_F

Определим, чему равняется энергия Ферми. Для этого рассмотрим газ при абсолютном нуле температуры. В этом случае интеграл от 0 до ∞ можно заменить на интеграл от 0 до E_F и учесть, что знаменатель дроби при нулевой температуре будет равен единице. Тогда получается

N = ∫f(E)dE = 2c₀VE_F^3/2 /3

E_F = (3N/2V)^2/3

T_F = (1/k)(3c₀N/2V)^2/3

Рассмотрим систему из Бозе-частиц. На эти частицы не распространяется принцип Паули. Среднее число таких частиц будет

E_l<N_l> = (e^(El-μ)/kT - 1)^-1

Так как на эти частицы не распространяется принцип Паули, то в основном состоянии с E₀ = 0 может быть сколько угодно частиц. В случае вырождения в заданном состоянии должно находится много частиц

<N₀> = (e^-μ/kT - 1)^-1

e^-μ/kT ≈ 1

Среднее число частиц, лежащих в заданном интервале, можно определить с помощью функции распределения Бозе

f(E)dE = c_oV(E)^1/2 dE/ (e^(E-μ)/kT - 1)

Но надо учесть, что сюда не входят частицы с энергией E = 0, так как для этих частиц функция распределения равна нулю.

∫ f(E)dE = Ne – частицы, энергия которых не равна нулю (возбужденные частицы)

Ne = ∫ c_oV(E)^1/2 dE/ (e^(E-μ)/kT - 1)

В случае вырождения e^-μ/kT = 1

Ne = ∫ c_oV(E)^1/2 dE/ (e^E/kT - 1) = c_oV (kT)^3/2 ∫x^1/2dx/(e^x-1) = c_o3V (kT)^3/2

Если газ вырожден, то число возбужденный частиц должно быть меньше полного числа частиц.

c_oV (kT)^3/2 << N

T << (1/k)(N/c_o3V)^2/3 = T_b – температура Бозе

Оказывается, что T_c, T_F, T_b практически определяется одинаковыми функциями.