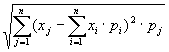Приложение 2.
ДОПОЛНИТЕЛЬНЫЙ ПЕРЕЧЕНЬ ЗАДАНИй ДЛЯ ПОДГОТОВКИ К ИСПЫТАНИЯМ
(для подготовки к Интернет-тестированию по курсу «Математика и информатика»)-
составляется в процессе подготовки студентов к Интернет-экзамену на основе использования учебных и экзаменационных тестовых заданий для студентов факультета специальной педагогики предшествующих 1-ых курсов ЛОГО-ОД, СУРДО-ОД, ОЛИГО-ОД ( начиная с 2009, 2010 и 2011 г.г.). в системе ФЕПО.
ДОМАШНИЕ задания для самостоятельной подготовки по курсу
«Математика и информатика»
( для студентов факультета специальной ПЕДАГОГИКИ )
Тема №1. Аксиоматическая теория .
1.1. К неопределяемым понятиям аксиоматического построения геометрии относятся…
-
луч, четырёхугольник
-
множество, точка, прямая
-
отрезок, угол
-
окружность, геометрическая фигура
1.2.Из приведенных высказываний истинным является следующее…
-

 В
аксиомах идет речь об основных
математических понятиях, таких как
«точка», «прямая», «плоскость».
В
аксиомах идет речь об основных
математических понятиях, таких как
«точка», «прямая», «плоскость».
-

 При
аксиоматическом построении какой-либо
теории некоторые аксиомы выводятся
путем доказательства из других аксиом
При
аксиоматическом построении какой-либо
теории некоторые аксиомы выводятся
путем доказательства из других аксиом
-

 Основные
понятия теории – это понятия, наиболее
часто используемые в этой теории.
Основные
понятия теории – это понятия, наиболее
часто используемые в этой теории.
-

 Любую
систему аксиом можно выбрать произвольно.
Любую
систему аксиом можно выбрать произвольно.
1.3. Среди предложенных математических утверждений аксиомой является следующие…
 Если
две прямые параллельны третьей, то они
параллельны.
Если
две прямые параллельны третьей, то они
параллельны.
 Если
две параллельные прямые пересечены
секущей, то накрест лежащие углы равны.
Если
две параллельные прямые пересечены
секущей, то накрест лежащие углы равны.
 Через
точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная
данной.
Через
точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная
данной.
 Если
прямая перпендикулярна одной из двух
параллельных прямых, то она перпендикулярна
и другой.
Если
прямая перпендикулярна одной из двух
параллельных прямых, то она перпендикулярна
и другой.
Тема №2. Теория множеств.
2.1 Установите соответствие между множествами и верными для них высказываниями. 1. А – множество студентов вашего вуза старше 17 лет 2. В – множество натуральных чисел, меньших 1 3. С – множество натуральных чисел, больших 1
-
множество бесконечно 3
-
 множество
является пустым
2
множество
является пустым
2 -
 множество
конечно
1
множество
конечно
1 -
 ничего
определенного о множестве сказать
нельзя
ничего
определенного о множестве сказать
нельзя
2. 2 Установите соответствие между множествами и верными для них высказываниями.
1. А – множество студентов первого курса; В – множество студентов
2. А – множество студентов; В – множество людей, умеющих водить машину
3. А – множество кошек; В – множество собак
-
множества А и В не пересекаются - 3
-
А является подмножеством В - 1
-
множества А и В равны
-
множества А и В пересекаются,ни одно из них не является подмножеством
другого - 2
2.3 Установите соответствие между множествами и верными для них высказываниями. 1. А – множество натуральных чисел, кратных 3; В – множество натурал. чисел, не кратных 3 2. А – множество натуральных чисел, кратных 6; В – множество натуральных чисел, кратных 2 3. А – множество натуральных чисел, кратных 2; В – множество четных натуральных чисел
-
В включено в А
-
 А
и В не
пересекаются
- 1
А
и В не
пересекаются
- 1 -
 А
является подмножеством
В - 2
А
является подмножеством
В - 2 -
 множества
А и В равны
- 3
множества
А и В равны
- 3
2.4.
![]() –
множество натуральных
чисел,
–
множество натуральных
чисел,
![]() –
множество
целых
чисел,
–
множество
целых
чисел,
![]() –
множество
рациональных
чисел,
–
множество
рациональных
чисел,
![]() –
множество
действительных
чисел.
Тогда истинны
следующие высказывания:
–
множество
действительных
чисел.
Тогда истинны
следующие высказывания:
-
Некоторые действительные числа являются рациональными -истина
-
Некоторые натуральные числа не являются действительными
-
Все натуральные числа являются целыми - истина
-
Все целые числа являются натуральными
2.5.
Даны два множества:
![]() –
интервал
числовой оси;
–
интервал
числовой оси;
![]() –
отрезок
числовой оси. Тогда для них истинными
высказываниями являются…
–
отрезок
числовой оси. Тогда для них истинными
высказываниями являются…
-
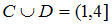 Истина
Истина -
 Истина
Истина -

-
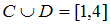
2.6.
Множества
А, В и С
изображены на диаграмме.
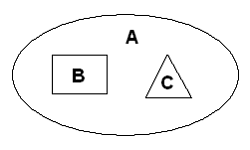 Тогда
для них верны следующие высказывания:
Тогда
для них верны следующие высказывания:
-

 A
A B=A
Истина
B=A
Истина -

 B
B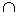 C=
C=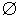 Истина
Истина -

 A
A B=B
B=B
-

 B
B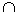 C=B
C=B
2.7
Даны множества
![]() и
и
![]() .
Тогда истинными
высказываниями являются…
.
Тогда истинными
высказываниями являются…
-
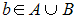 Истина
Истина -

-
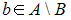
-
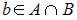 Истина
Истина
1.8.
Заданы множества
![]() и
и
![]() .
Верным
для них будет утверждение…
.
Верным
для них будет утверждение…
-
Множества А и В равны
-
Множество В есть подмножество множества А
-
Множество А есть подмножество множества В Истина
-
Множества А и В не содержат одинаковых элементов
1.9. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
-
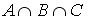 1
1 -
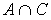 2
2 -
A 3
-
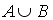 4
4
1.10.
Если отношение задано неравенством:
![]() ,
то данному отношению принадлежит
следующие пары чисел…
,
то данному отношению принадлежит
следующие пары чисел…
-
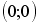
-
(4;5) истина
-
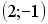
-
 истина
истина
1.11. Даны множества M={ a, b, c, d} и N={b, c, d, e, f, g}. Установите соответствия между обозначениями множеств и самими множествами. Обозначения множеств:
1.
M![]() N
2.
M
N
2.
M![]() N
3.
M\N
4. N\M
N
3.
M\N
4. N\M
Множества:
{a} - 3
{b, c, d} - 1
{a, b, c, d, e, f, g} - 2
{e, f, g} - 4
11.12.
Заданы множества
![]() {2,6,-6}
и
{2,6,-6}
и
![]() {4,-4},
тогда декартовым
произведением
этих множеств АВ
является множество…
{4,-4},
тогда декартовым
произведением
этих множеств АВ
является множество…
{(4, 6), (6, 4), (6, -4), (-6, -4), (4, -6), (-4, 2)}
{-6, -4, 2, 4, 6}
{![]() }
}
{(2, 4), (2, -4), (6, 4), (6, -4), (-6, 4), (-6, -4)} истина
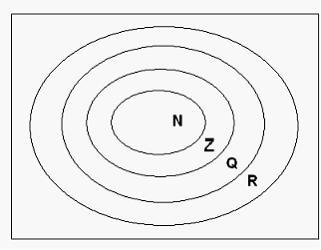
11.13. Принято обозначать: N-множество натуральных чисел; Q-множество рациональных чисел; Z-множество целых чисел; R-множество действительных чисел. Тогда верным утверждением будет…
![]() истина
истина
![]()
![]()
![]()
11.14. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
![]() 2
2
![]() 5
5
![]() 6
6
![]() 1
1
![]() 3
3
![]() 4
4
11.15 Даны множества N={ a, b, c, d, e, f, g} и K={a, b, c, d, e}. Установите соответствия между обозначениями множеств и самими множествами.
1.
N![]() K
K
2.
N![]() K
K
3. N\K
4. K\N
Множества:
{a, b, c, d, e} 1
{a, b, c, d, e, f, g} 2
{f, g} 3
{ } 4
11.16
Заданы множества
![]() {1,-3} и
{1,-3} и
![]() {-а,
в}, тогда декартовым
произведением
этих множеств АВ
является множество …
{-а,
в}, тогда декартовым
произведением
этих множеств АВ
является множество …
{(1,-a), (1, в), (-3,-а), (-3, в)} - истина
{(-а,1),(в,-3),(в,1),(-а,-3)}
{-а, в, 1, -3}
{![]() }
}
11.17.
Заданы множества
![]() {8,3} и
{8,3} и
![]() {5,6},
тогда декартовым
произведением
этих множеств АВ
является множество …
{5,6},
тогда декартовым
произведением
этих множеств АВ
является множество …
{(8,5), (8,6), (3,5), (3,6)} - истина
{(5, 8), (5, 3), (6, 8), (6, 3)}
{3, 5, 6, 8}
{![]() }
}
Тема №3. Комбинаторика
-
ПИз цифр числа 4689 можно составить различные трехзначные числа, в которых цифры не повторяются.
Всего таких чисел будет... 60р24
2оа24
-
Число различных перестановок из букв слова «зачет», в которых буква «з» стоит на первом месте, а буква «т» на последнем месте, равно… 6.
-
Количество различных способов выбора (порядок не имеет значения) 2 различных учебников по математической логике из 6 различных, имеющихся в библиотеке, равно… 15 С 2/6
-
Количество перестановок из букв слова «вальс», в которых буква «в» на первом месте, а буква «с» - в конце слова, равно…
-
24
-
3
-
6 истина
-
5
3.5. Количество перестановок из букв слова «лидер», в которых буква «е» на первом месте, а буква «д» - в конце слова равно…. 6
3.6. .Количество перестановок из букв слова «вирус», в которых буква «в» на первом месте равно….24
3.7. Количество перестановок из букв слова «время», в которых буква «я» на первом месте равно….24
Тема № 4. Алгебра высказываний.
![]()
![]() 4.1.
Даны высказывания: А = «число делится
на 2» и В = «число является четным».
Высказывание «Если
число делится на 2, то оно является
четным»
представляет собой _________ высказываний
А и В.
4.1.
Даны высказывания: А = «число делится
на 2» и В = «число является четным».
Высказывание «Если
число делится на 2, то оно является
четным»
представляет собой _________ высказываний
А и В.
-
конъюнкцию
-
эквиваленцию
-
дизъюнкцию
-
импликацию
4.2 Даны высказывания: А = «Озеро Байкал является самым чистым озером в мире» и В = «Чайковский написал 10 опер». Дизъюнкцией этих высказываний является предложение…
-
Если озеро Байкал является самым чистым озером в мире, то Чайковский написал 10 опер»
-
«Озеро Байкал является самым чистым озером в мире тогда и только тогда, когда Чайковский написал 10 опер»
-
«Озеро Байкал является самым чистым озером в мире, и Чайковский написал 10 опер»
-
«Озеро Байкал является самым чистым озером в мире, или Чайковский написал 10 опер»
4.3.
Высказывание A
– «Джон фон Нейман – архитектор ЭВМ»;
высказывание В
– «Диагонали прямоугольника равны».
Конъюнкцией
этих высказываний (![]() )
является предложение …
)
является предложение …
-
«Если Джон фон Нейман – архитектор ЭВМ, то диагонали прямоугольника равны»
-
«Джон фон Нейман – архитектор ЭВМ, и диагонали прямоугольника равны» истина
-
«Джон фон Нейман – архитектор ЭВМ, или диагонали прямоугольника равны»
-
«Джон фон Нейман – архитектор ЭВМ тогда и только тогда, когда диагонали прямоугольника равны»
4.4..
Известно, что длина прямоугольника
![]() см,
ширина –
см,
ширина –
![]() см.
Тогда истинными высказываниями являются
следующие…
см.
Тогда истинными высказываниями являются
следующие…
![]()
![]()
 Периметр
прямоугольника есть число иррациональное.
- истина
Периметр
прямоугольника есть число иррациональное.
- истина
![]()
![]()
 Площадь
прямоугольника есть число рациональное.
-истина
Площадь
прямоугольника есть число рациональное.
-истина
![]()
![]()
 Периметр
прямоугольника есть число рациональное.
Периметр
прямоугольника есть число рациональное.
![]()
![]()
 Площадь
прямоугольника есть число иррациональное.
Площадь
прямоугольника есть число иррациональное.
4.5.
Высказывание A
– «Алгебра логики изучает высказывания»;
высказывание В
– «Сумма углов треугольника равна
![]() ».
Конъюнкцией
этих высказываний (
».
Конъюнкцией
этих высказываний (![]() )
является предложение …
)
является предложение …
-
Алгебра логики изучает высказывания, и сумма углов треугольника равна
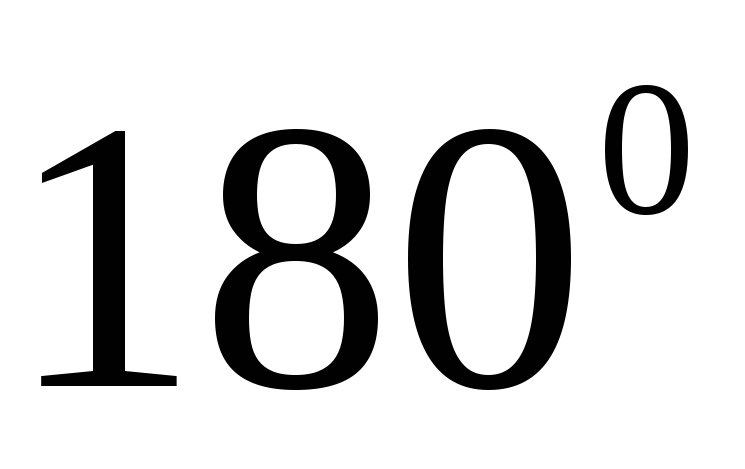 -истина
-истина -
Алгебра логики изучает высказывания, или сумма углов треугольника равна

-
Если алгебра логики изучает высказывания, то сумма углов треугольника равна

-
Алгебра логики изучает высказывания тогда и только тогда, когда сумма углов треугольника равна
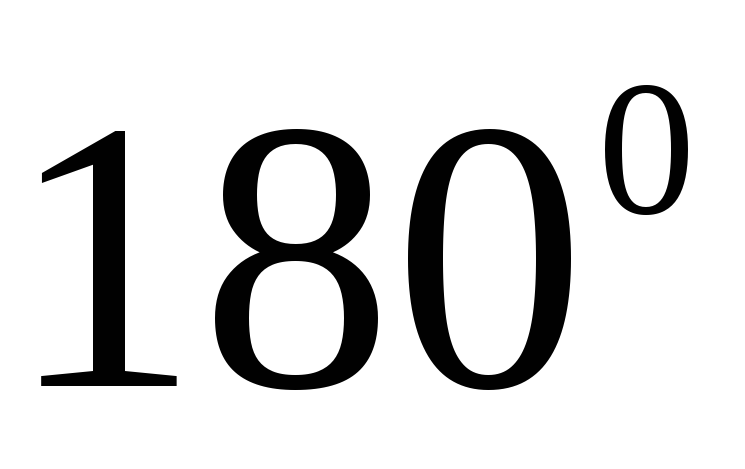
4.6.
Высказывание A
– «Принтер – это устройство вывода
информации»; высказывание В
– «Две параллельные прямые не имеют
общих точек». Дизъюнкцией
этих высказываний (![]() )
является предложение …
)
является предложение …
-
Принтер - это устройство вывода информации, или две параллельные прямые не имеют общих точек -истина
-
Принтер - это устройство вывода информации, и две параллельные прямые не имеют общих точекЕсли принтер - это устройство вывода информации, то две параллельные прямые не имеют общих точекПринтер - это устройство вывода информации тогда и только тогда, когда две параллельные прямые не имеют общих точек
Тема № 5. Теория вероятностей. Случайные события.
5.1.
Пусть A
и B
- несовместные
события. Тогда
![]() равно…
равно…![]()
![]()
-
1
-
0
-
-0,5
-
1,5
5.2 Попадание и промах при одном выстреле являются событиями…
-
несовместными
-

 независимыми
независимыми
-

 не
противоположными
не
противоположными
-

 совместными
совместными
5.3. Вероятность выпадения четной цифры при одном подбрасывании игрального кубика равна…
-

-
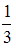
-
0,5 - истина
-

5.4. Из слова «АБРИКОС» выбирается наугад одна буква. Вероятность того, что это гласная буква, равна…
-
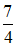
-



-



-


 -истина
-истина
5.5. Вероятность выпадения нечетной цифры при одном подбрасывании игрального кубика равна…
-

-

 0,5
-истина
0,5
-истина -



-


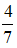
5.6. Подбрасывается игральный кубик. Подсчитывается число очков, выпавших на верхней грани кубика. Пусть дискретная случайная величина X – число выпавших очков на верхней грани кубика. Тогда вероятности ее возможных значений равны одному и тому же числу …
-

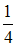
-


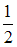
-


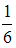 - истина
- истина -



5.7 Симметричная монета подбрасывается один раз. Пусть случайная величина X – число выпавших гербов. Тогда вероятности возможных значений X равны …
-
 -истина
-истина -

 1
1
-



-



5.8. Для вычисления дисперсии дискретной случайной величины используется формула…
-
 -
истина
-
истина
5.9. Из приведённых величин случайными являются…
-
«Число бракованных деталей в прибывшей на завод партии» - истина
-
«Число p=3,1415927»
-
«Число дней в декабре»
-
«Число очков при стрельбе по мишени» - истина
5.10. Вероятность наступления некоторого события не может быть равна...
-
0,3
-
1
-
1,3 -истина
-
0,7
5.11. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, не меньшее 4, равна …
-
 -
истина
( 1/6 х 1/6)
-
истина
( 1/6 х 1/6) -
-
 1
1 -

-

-
5.12. В студии телевидения 2 телевизионные камеры. Вероятность того, что в данный момент работает первая камера, равна 0,6, а вторая камера – 0,9. Тогда вероятность того, что в данный момент работает хотя бы 1 камера (событие А) равна …
![]()
![]()
 1,5
1,5
![]()
![]()
 0,96
-истина
Р=1-0,4х0,1=1-0,04=0,96
0,96
-истина
Р=1-0,4х0,1=1-0,04=0,96
![]()
![]()
 0,5
0,5
![]()
![]()
 0,46
0,46
5.13. В бригаде каменщиков имеется 2 звена: в первом звене 4 квалифицированных каменщика и 2 подсобных, во втором звене 3 квалифицированных каменщика и 2 подсобных. Бригадир наугад выбрал одно из звеньев, а затем аналогично выбрал каменщика. Тогда вероятность того, что этот каменщик оказался квалифицированным, равна …
![]()
![]()

![]() -истина
Р= 1/2 х(4/6+3/5) =1/2 х38/30= 19/30
-истина
Р= 1/2 х(4/6+3/5) =1/2 х38/30= 19/30
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()

![]()
5.14.
Исходом,
благоприятствующим
событию «выпало нечетное
число очков» при подбрасывании игрального
кубика, является цифра…
![]()
![]()
![]()
 2
2
![]()
![]()
 6
6
![]()
![]()
 1
-истина
1 - соответствует нечетному
числу очков
1
-истина
1 - соответствует нечетному
числу очков
![]()
![]()
 4
4
5.15. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников, 7 третьекурсников. Из этого состава наудачу выбирают 5 человек на предстоящую конференцию. Вероятность того, что будут отобраны одни третьекурсники, равна…
![]()
![]()

![]()
![]()
![]()

![]() -истина
Р= С
5/7
: С
5/15
-истина
Р= С
5/7
: С
5/15
![]()
![]()

![]()
![]()
![]()

![]()
5.16. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, большее 2, равна … 1/9 (2/6 х 2/6) для 4 и 6
5.17. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет нечетное число очков, не большее 5, равна …1/4 (1/2х1/2) для 1 и 3
5. 18. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет нечетное число очков, большее 3, равна … 1/36 (1/6х1/6) для 5
5.19. Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, не большее 4, равна … 1/9
5.20. Выберите несовместные события А и В.
-
А – «Появление 6 при бросании игральной кости», В – «Появление 4 при бросании игральной кости» истина
-
А – «Наступление ночи», В – «Восход солнца» истина
-
А – «Выбивание менее 5 очков при стрельбе по мишени», В – «Выбивание от 7 до 10 очков при стрельбе по мишени» истина
-
А – «Выбивание менее 5 очков при стрельбе по мишени», В – «Выбивание четного числа очков при стрельбе по мишени»
-
А – «Орел вверху при бросании монеты», В – «решка вверху при бросании монеты» истина
-
А – «Наступление зимы», В – «Выпадение снега»
-
А – «Появление дамы при выборе карты из колоды», В – «Появление бубновой масти при выборе карты из колоды»
5.21. Выберите совместные события А и В.
-
А – «Выбивание менее 4 очков при стрельбе по мишени», В – «Выбивание нечетного числа очков при стрельбе по мишени» истина
-
А – «Появление 6 при бросании игральной кости», В – «Появление четного числа при бросании игральной кости» истина
-
А – «Наступление шторма», В – «Наступление штиля»
-
А – «Выбор на экзамене билета с номером 13», В – «Выбор на экзамене билета с четным номером»
-
А – «Наступление зимы», В – «Выпадение снега» истина
-
А – «Появление туза при выборе карты из колоды», В – «Появление бубновой масти при выборе карты из колоды» истина
-
А – «Орел вверху при бросании монеты», В – «решка вверху при бросании монеты»
-
А – «Появление туза при выборе карты из колоды», В – «Появление короля при выборе карты из колоды»
5.23. Выберите достоверные события.
-
А – выбор черного шара из урны с черными шарами истина
-
А – наступление в Москве лета после весны истина
-
А – замерзание воды в реке при температуре +30C
-
А – выпадение 6 очков при выбрасывании игральной кости
5.24. Выберите невозможные события.
-
А – замерзание воды в реке при температуре +30C - истина
-
А – выбор черного шара из урны с белыми шарами -истина
-
А – наступление лета после весны
-
А – выпадение 6 очков при выбрасывании игральной кости
5.25. Выберите случайные события.
-
А – выпадение 6 очков при выбрасывании игральной кости -истина
-
А – выбор черного шара из урны с белыми и черными шарами -истина
-
А – выбор белого шара из урны с белыми шарами
-
А – выбор черного шара из урны с белыми шарами
5.26. Вероятность наступления равна 0 для событий …
-
А – выбор синего шара из урны с белыми шарами -истина
-
А – выращивание ананасов на ёлке в Сибирской тайге -истина
-
А – покупка выигрышного лотерейного билета
-
А – выбор синего шара из урны с синими шарами
5.27. Вероятность наступления равна 1 для событий …
-
А – выбор синего шара из урны с синими шарами - истина
-
А – закипание воды в чайнике при температуре +100C и выше -истина
-
А – наступление 32 июня
-
А – выбор синего шара из урны с синими и красными шарами
5.28. Вероятность наступления некоторого события не может быть равна ...
2 истина
0
1
![]()
1,9 истина
0,9
1,8 истина
0,8
1,7 истина
0,7
0,3
3 истина
-1,6 истина
0,5
4 истина
-0,4 истина
5.29. В поле работают независимо друг от друга 2 комбайна. Вероятность выхода из строя первого комбайна равна 0,1, второго – 0,2. Тогда вероятность выхода из строя обоих комбайнов равна …
![]()
![]()
 0,02
( 0,1х 0,2)
0,02
( 0,1х 0,2)
![]()
![]()
 0,002
0,002
![]()
![]()
 0,3
0,3
![]()
![]()
 0,1
0,1
5.30.
На сборку компьютеров поступают чипы от 2 поставщиков: 60 % от первого и 40% от второго. Брак в изготовлении чипов первого поставщика составляет 3%, а второго – 2%. Вероятность того, что взятый наудачу чип окажется бракованным, равна …
![]()
![]()
 0,024
0,024
![]()
![]()
 0,026
( 0,03 х0,6 + 0,02х0,4)
0,026
( 0,03 х0,6 + 0,02х0,4)
![]()
![]()
 2,6
2,6
![]()
![]()
 1,44
1,44
![]()
![]()
![]()
![]()
Тема№ 6. Частотный анализ случайных событий
6.1. Из 38 вопросов, предложенных студенту при тестировании, он ответил правильно на 31 вопрос. Тогда относительная частота неправильных ответов студента равна…
-
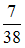 истина
истина -
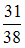
-
1178
-
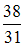
5.4. Из 1000 заемщиков кредитов банка не вернули кредит 120 клиентов. Тогда относительная частота не возврата кредитов в банке равна
-
120000
-

 0,88
0,88
-

 0,120
истина
( 120
0,120
истина
( 120

 :
1000
)
:
1000
)
6.3 Из 31 дня июля 10 дней были дождливыми. Тогда относительная частота дождливых дней в июле равна …
-


-

 41
41
-


 -истина
-истина -

 310
310
Тема №7. Теория вероятностей. Случайные величины.
5.22. Выберите дискретные случайные величины X.
-
X – число очков, выпадающих при бросании игральной кости истина
-
X – количество мальчиков, рожденных за тот или иной год истина
-
X – значение функции f(x)=x на множестве действительных чисел
-
X – отклонение размера детали (некоторый интервал) от величины, требуемой ГОСТом
6.4.
В результате некоторого эксперимента
получен статистический ряд:
 Тогда
значение относительной частоты при
Тогда
значение относительной частоты при
![]() будет
равно…
будет
равно…
-
0,1
-
0,4 - истина (1- 0,6)
-
0,5
-
0,2
Тема № 8. Плотность вероятности и нормальный закон распределения случайных величин
7.1.
Вес арбузов подчиняется нормальному
закону распределения с плотностью 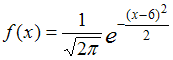 .
Тогда математическое
ожидание веса арбузов
равно …
.
Тогда математическое
ожидание веса арбузов
равно …
-
0
-

 6
-истина
6
-истина -

 2
2
-

 1
1
7.2Случайная
величина X задана функцией
распределения
![]() .
Тогда плотность
распределения вероятностей
случайной величины X
имеет вид …
.
Тогда плотность
распределения вероятностей
случайной величины X
имеет вид …
-
 истина
истина -



-


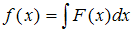
-


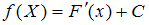
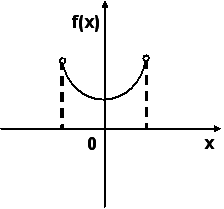
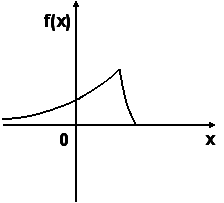
7.9. График плотности вероятностей для нормального распределения изображен на рисунке...
-
2)
-

-
3)
-
 Истина
Истина
-
4)
-
Тема № 9 . Характеристики и ряды распределения случайных величин.
8.1.
Математическое
ожидание
дискретной случайной величины, заданной
законом распределения
![]() равно…
равно…
-
3,1
-

 3,3
-истина
(2х0,2+3х0,3+4х0,5)
3,3
-истина
(2х0,2+3х0,3+4х0,5) -

 1,1
1,1
-

 3,2
3,2
8.2.
Математическое
ожидание случайной величины
![]() характеризует…
характеризует…
концентрацию возможных значений X относительно центра распределения
-
центр распределения истина
-
максимальное возможное значение случайной величины X
-
рассеивание возможных значений X относительно центра распределения
8.3.
Закон распределения вероятностей
задается таблицей
![]() при
при
![]() ,
равном
…
,
равном
…
-
0,3
-

 0,98
0,98
-

 0,7
истина
(1 - 0,3)
0,7
истина
(1 - 0,3) -
8.4. Дискретная случайная величина Х имеет закон распределения вероятностей:
![]()
Математическое ожидание М(Х) этой случайной величины равно ...2,8
8.5. Дискретная случайная величина Х имеет закон распределения вероятностей:
![]()
Математическое ожидание М(Х) этой случайной величины равно 1,3
8.6. Дискретная случайная величина Х имеет закон распределения вероятностей:
![]()
Математическое ожидание М(Х) этой случайной величины равно ...4,4
Тема № 10. Математическая статистика.
10.1
Для статистического ряда
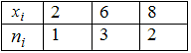 мода
равна …
мода
равна …
-
3
-

 8
8
-

 6
- истина
6
- истина -

 2
2
10.2.
Объем
выборки
по заданной
гистограмме
частот
равен …

-
25
-

 24
24
-

 12
--истина
( 1+4+5+2)
12
--истина
( 1+4+5+2) -

 4
4
10.2. Медиана вариационного ряда 3 5 6 7 8 9 равна…