4.2.2 Общее решение неоднородных уравнений

Уравнения состояния линейной стационарной системы задаются согласно (4.7) в виде

= Аx + Br,

y = Cx + Dr.

Матрица А в этих уравнениях – основная матрица системы, так как ее структура определяет переходную матрицу состояния. От этой матрицы зависит как вынужденная (установившаяся), так и переходная составляющие решения. Матрица В – матрица связи: структура этой матрицы определяет характер связи входных воздействий с переменными состояния. Матрица С – также матрица связи, а именно, связи переменных состояния с выходными переменными системы. Наконец, матрица D – опять матрица связи; на этот раз связи входных переменных непосредственно с выходными переменными. Часто для реальных систем D является нулевой матрицей, так что связь входа непосредственно с выходом отсутствует.

Как и в скалярном случае, общее решение уравнений (4.7) для х(t) и y(t) можно получить разными методами. Например, как это сделать с помощью метода вариации параметров, рассмотрено ниже.

Соответствующее однородное дифференциальное уравнение (4.12) имеет решение х₀(t) = Ф(t – t₀)x(t₀) при tt₀. Подобно формуле (1.28) частное решение ищем в виде х_Н(t) = Ф(t –t₀)U(t)x(t₀). Тогда общее решение неоднородного уравнения (4.7) равно

x(t) = x₀(t) + x_H(t) = Ф(t – t₀)x(t₀) + Ф(t – t₀)U(t)x(t₀).

Удобнее это уравнение записать в форме

x(t) = Ф(t – t₀)(E + U(t))x(t₀) = Ф(t – t₀)z(t), (4.20)

где подлежит определению неизвестный пока вектор z(t) = (E + U(t))x(t₀).

Подставляя уравнение (4.20) в уравнение (4.7), получим

Так как переходная матрица удовлетворяет однородному уравнению (4.11), первое слагаемое в последнем выражении равно нулю и получаем

(4.21)

Интегрируя уравнение (4.21) в пределах от t₀ до t, имеем

(4.22)

Учитывая, что z(t₀) = x(t₀), из уравнений (4.20) и (4.22) находим x(t)

Поскольку

окончательно получаем

(4.23)

Решение для у(t) следует из подстановки уравнения (4.23) в уравнение выхода (4.7)

(4.24)

Выражения (4.23) и (4.24) являются решениями уравнений состояния (4.7). Первое слагаемое в уравнении (4.23) представляет собой переходную составляющую решения, обусловленную начальными условиями, тогда как второе слагаемое (по сути, это интеграл свертки) является вынужденной составляющей, зависящей от входного воздействия.

4.3 Обыкновенные уравнения нестационарных систем

4.3.1 Переходная нестационарная матрица

Если параметры системы изменяются во времени, то элементы матрицы А не являются постоянными, а являются функциями времени. В этом случае однородное векторно - матричное дифференциальное уравнение имеет вид

(4.24)

При решении этого уравнения естественно обратиться к скалярной аналогии, то есть к скалярному уравнению

(4.25)

Решение уравнения (4.25) равно

(4.26)

где t₀ – некоторый начальный момент времени.

По аналогии с формулой (4.26) решение матричного уравнения (4.24) предполагается в виде

(4.27)

Но при подстановке выражения (4.27) в уравнение (4.24) видно, что формула (4.27) действительно представляет собой решение в том и только в том случае, если

(4.28)

где

К сожалению, условие (4.28) выполняется не всегда; более того, оно чаще не выполняется, чем выполняется. В двух частных, но тривиальных случаях уравнение (4.28) выполняется всегда, - это: матрица А – постоянная или А – диагональная матрица. Решение для первого случая уже разбиралось, а во втором случае уравнения состояния оказываются не связанными друг с другом, так что для каждого x_i годится решение (4.26).

Можно показать, что условие (4.28) трансформируется в условие коммутативности для матрицы А

А(t₁) А(t₂) = А(t₂) А(t₁) для всех t₁ и t₂. (4.29)

Таким образом, если выполняется уравнение (4.29), то выражение (4.27) является решением уравнения (4.24) и переходная матрица состояния (зависящая уже от двух аргументов t и t₀) равна

(4.30)

Если условие коммутативности (4.29) не выполняется, переходная матрица уже не может выражаться уравнением (4.30). Тогда решение уравнения (4.24) можно получить методом, известным как метод интегрирования Пеано – Бэкера. Этот метод заключается в следующем.

При заданных начальных условиях x(t₀) проинтегрируем уравнение (4.24)

(4.31)

Это уравнение можно встретить под названием векторного интегрального уравнения Вольтерра. Решается это уравнение путем последовательных подстановок правой части уравнения (4.31) в подинтегральное выражение вместоx(t). Например, первая итерация даст

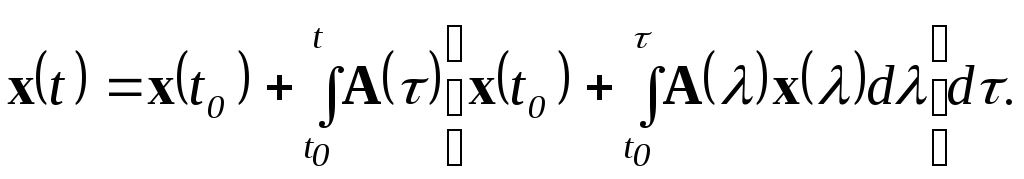(4.32)

Упростить запись подобных выражений можно введением оператора интегрирования Q(..) = . Тогда уравнение (4.31) можно записать в виде

x(t) = x(t₀) + Q(Аx),

а уравнение (4.32) приобретает вид

x(t) = x(t₀) + Q(А)x(t₀) + Q(АQ(Аx)).(4.33)

Продолжая процедуру, описываемую уравнением (4.33), получим х(t)в видеряда Неймана

x(t) = [E + Q(А) + Q(АQ(А)) + Q(АQ(АQ(А))) + …]x(t₀). (4.34)

Первое слагаемое в скобках – это единичная матрица. Второе слагаемое равно интегралу от А(t)в пределах отt₀доt. Третье слагаемое получается умножениемQ(А)наАслева и последующим интегрированием произведения в пределах отt₀доtи т.д. Если элементы матрицыАограничены на отрезке интегрирования, то бесконечный ряд сходится равномерно и абсолютно к некоторой квадратной матрицеG(А),называемойматрицантом:

G(А) = E + Q(А) + Q(АQ(А)) + Q(АQ(АG(А))) +…. (4.35)

Основное свойство матрицанта заключается в том, что

(4.36)

Это свойство нетрудно доказать, если взять производную по tот обеих частей выражения (4.35).

Выражение (4.34) совместно со свойством (4.36) дают основание утверждать, что G(А)представляет собой искомую переходную матрицу состояния нестационарной системы:

Ф(t, t₀) = G(А).(4.37)

Понятно, что при постоянной матрице Аиз выражения (4.35) следует, что

Недостаток этого метода очевиден: при медленной сходимости ряда (4.35) процесс вычисления достаточно трудоемок.

Во многих случаях переходная матрица легко получается при надлежащем выборе переменных состояния. Может оказаться полезным определить, существуют ли такие переменные состояния, чтобы было правомерным применение соотношения (4.30).

Сведем воедино свойства переходных матриц, часть из которых уже отмечалась.

Свойство 1.

Ф(t, t) = E.(4.38)

Это свойство следует из определения переходной матрицы.

Свойство 2.

Ф(t₁, t₂) Ф(t₂, t₃) = Ф(t₁, t₃).(4.39)

Воспользуемся соотношениями

x(t₂) = Ф(t₂, t₃)x(t₃)и

x(t₁) = Ф(t₁, t₂)x(t₂) = Ф(t₁, t₃)x(t₃).

Подставив первое из них во второе, получим

x(t₁) = Ф(t₁, t₂) Ф(t₂, t₃)x(t₃) = Ф(t₁, t₃) x(t₃),

откуда с неизбежностью следует соотношение (4.39).

Свойство 3.

Ф(t₁, t₂) = Ф^-1(t₂, t₁).(4.40)

Это свойство вытекает из свойства 2, если вместо t₃в формулу (4.39) подставитьt₁. Получим

Ф(t₁, t₂) Ф(t₂, t₁) = Ф(t₁, t₁) = E

или, умножая справа на Ф^-1(t₂, t₁), имеем формулу (4.40).

Свойство 4. (для стационарных систем).

Ф(t + ) = Ф(t) Ф().(4.41)

Это свойство следует непосредственно из свойств матричной экспоненты, поскольку Ф(t) = e^Аt.

Свойство 5.(для стационарных систем).

Ф^-1(t) = Ф(-t). (4.42)

Это свойство является непосредственным следствием свойства 3 в применении к стационарным системам или вытекает из формулы (4.41), если в последнюю подставить  = -t.