2. Квантовая механика и атомная физика

2.1. Квантовая механика

Квантовая механика – раздел механики, который изучает законы движения микрочастиц. Положение микрочастицы в пространстве можно описывать только вероятностным образом: ставится вопрос о вероятности нахождения частицы в определенной области пространства.

Функция координат и времени (х, t), квадрат модуля которой определяет вероятность нахождения частицы в интервале координат от х до х + dх (dр) называется волновой функцией частицы:

dp = | |² dx (2.1)

Таким образом, квадрат модуля волновой функции имеет смысл плотности вероятности: вероятность, отнесенную к единице длины:

(2.2)

Вероятность нахождения частицы в интервале координат от х₁ до х₂ определяется формулой:

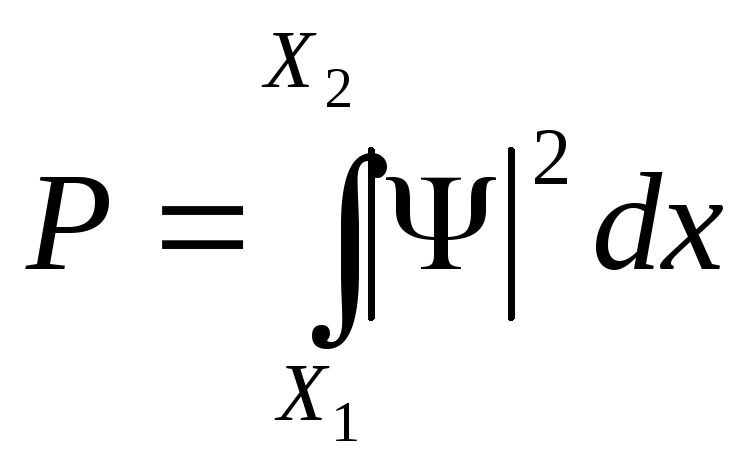(2.3)

Уравнение, которое позволяет найти волновую функцию частицы, называется уравнение Шредингера:

(2.4)

где m – масса частицы; ; U – потенциальная энергия частицы.

Если частица находится в стационарном потенциальном поле, то вероятность ее нахождения в различных областях пространства не зависит от времени. Такое состояние частицы называется стационарным. В случае стационарных состояний уравнение Шредингера принимает вид:

, (2.5)

где Е – полная механическая энергия частицы.

Уравнение (2.5) называется стационарным уравнением Шредингера.

Волновая функция частицы должна удовлетворять стандартным условиям: она должна быть однозначной, конечной, непрерывной и иметь непрерывную первую производную. Первые два требования обусловлены тем, что волновая функция определяет величину вероятности нахождения частицы в различных областях пространства. Вторые два условия связаны с видом уравнения Шредингера, в которое входит вторая производная волновой функции. Волновая функция должна также удовлетворять условию нормировки:

Если частица находится в бесконечно глубокой прямоугольной потенциальной яме шириной ℓ (рис. 5), потенциальная энергия частицы U в интервале координат 0  x  ℓ равна нулю и обращается в бесконечность при x < 0 и x > ℓ.

U

Рис. 2

n = 5

n = 4

n = 3

n = 2

n = 1

Стационарное уравнение Шредингера в этом случае принимает вид:

,

где Е – кинетическая энергия частицы.

Решением этого волнового уравнения является функция:

(2.6)

где n = 1; 2; ...... любое целое положительное число, которое называется квантовым числом. А кинетическая энергия частицы равна

, (2.7)

то есть энергетический спектр частицы в бесконечно глубокой потенциальной яме является дискретными. Значения энергии, которые может иметь микрочастица, называют энергетическими уравнениями.

Разность энергий двух соседних энергетических уровней

растет с ростом номера уровня. Плотность вероятности в данном случае:

(2.8)

А вероятность нахождения частицы в интервале координат от x₁ до x₂ определяется выражением:

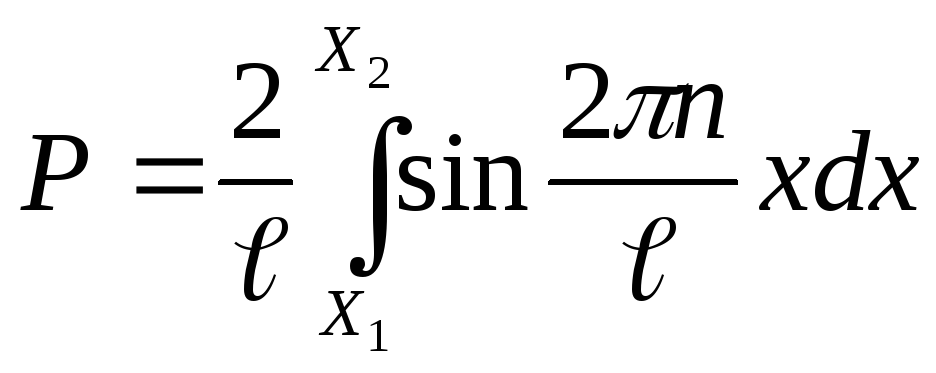(2.9)

Для нахождения первообразной необходимо сделать замену:

,

и выражение (2.9) примет вид:

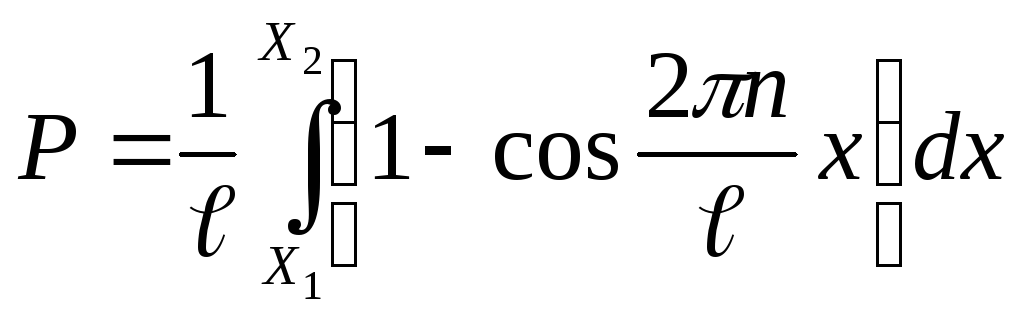(2.10)

Пример 4. Частица находится в одномерной, прямоугольной, потенциальной яме на пятом энергетическом уровне. Определить, в каких точках интервала 0  x  ℓ плотность вероятности нахождения частицы имеет максимальные и минимальные значения. Рассчитать вероятность нахождения частицы в интервале .

Плотность вероятности равна квадрату модуля волновой функции. В данном случае:

,

так как частица находится на пятом энергетическом уровне, n = 5 и

. (2.11)

Из формулы (2.11) следует, что плотность вероятности будет максимальный, если

, то есть если (2.12)

где m = 0; 1; 2;.......

Из полученной формулы (2.12) получают выражение для координат точек, в которых плотность вероятности максимальна:

.

Следовательно:

Плотность вероятности будет равна нулю (минимальное значение) в точках, в которых

, то есть ,

где m = 0; 1; 2;....

Следовательно:

Задавая значения координаты x в долях ℓ и подставляя их в формулу (2.11) получают график зависимости плотности вероятности от координаты (рис. 6)

│Ψ│²

Вероятность нахождения частицы в интервале координат

находят по формуле (2.9):