
- •Информатика
- •Утверждено редакционно-издательским советом университета
- •О структуре курса
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1. Содержание дисциплины по гос Для технических, экономических и гуманитарных специальностей
- •Для направления подготовки «Автоматизация и управление»
- •1.2.2. Объем дисциплины и виды учебной работы
- •1.2.3. Перечень видов практических занятий и видов контроля
- •Рабочие учебные материалы
- •2.1. Рабочая программа (объем дисциплины 220 часов)
- •Раздел 1. Введение. Информация и информатика
- •(12 Часов)
- •Раздел 2. Вычислительная техника (8 часов )
- •Раздел 3. Программное обеспечение компьютеров (32 часа)
- •(40 Часов)
- •(32 Часа)
- •Раздел 9. Информационные системы и информационное общество ( 8 часов)
- •2.2. Тематический план дисциплины
- •2.2.1. Тематический план дисциплины для студентов очной формы обучения
- •2.2.2. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.3. Тематический план дисциплины для студентов заочной формы обучения
- •2.3. Структурно-логическая схема дисциплины “Информатика” (Первый семестр)
- •Информатика, ч.1
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Редактирование и форматирование документов
- •Локальные и глобальные сети. Интернет. Основные понятия
- •Структурно-логическая схема дисциплины “Информатика” (Второй семестр)
- •Информатика, ч.2
- •Раздел 8
- •Раздел 9
- •2.4. Практический блок
- •Лабораторный практикум (очная форма обучения)
- •Лабораторный практикум (очно-заочная форма обучения)
- •Лабораторный практикум (заочная форма обучения)
- •2.5. Временной график изучения дисциплины
- •Балльно-рейтинговая система
- •Информационные ресурсы дисциплины
- •3.1. Библиографический список Основной:
- •Дополнительный:
- •3.2. Опорный конспект по дисциплине * введение
- •Раздел 1. Информация и информатика
- •При работе с данным разделом Вам предстоит:
- •Понятие об информации. Кодирование информации
- •1.1.5. Представление чисел в научном (экспоненциальном) формате
- •Файлы и файловая структура
- •Раздел 2. Вычислительная техника
- •При работе с данным разделом Вам предстоит:
- •2.1. Электронные вычислительные машины, основные устройства, этапы и тенденции развития
- •2.2. Базовая аппаратная конфигурация персонального компьютера
- •Монитор
- •Оперативная память
- •Раздел 3. Программное обеспечение компьютеров
- •При работе с этим разделом необходимо:
- •3.1. Системные и прикладные программы
- •3.2. Языки программирования. Алгоритм и программа. Компиляторы и интерпретаторы
- •3.3. Защита и резервирование информации
- •Раздел 4. Сетевые технологии обработки информации
- •В процессе работы с разделом Вам предстоит:
- •4.1. Локальные и глобальные сети. Интернет. Основные понятия
- •4.2. Услуги и адресация Интернета. Электронная почта
- •Раздел 5. Создание текстовых и графических документов
- •5.1. Редактирование и форматирование документов
- •5.2. Работа с таблицами и формулами
- •5.3. Схемы и диаграммы в Word и Writer
- •Раздел 6. Обработка данных средствами электронных таблиц (эт)
- •В процессе работы с разделом Вам предстоит:
- •6.1. Табличные процессоры и их характеристики
- •Имена строк – это их номера. В каждой электронной таблице более 65000 строк.
- •6.2. Копирование формул. Абсолютные и относительные адреса ячеек
- •Пример 2
- •Пример 3
- •Пример 4
- •Пример 5
- •Пример 6
- •Пример 7
- •Пример 8
- •6.3. Работа с функциями электронных таблиц
- •Пример 1
- •Пример 2 Вычислить
- •Пример 3
- •Пример 4
- •Раздел 7. Реализация в эт управленческих и экономических задач
- •В процессе работы с разделом Вам предстоит:
- •7.1. Системы принятия решений (экспертные системы) (Тема изучается студентами всех специальностей, кроме 080502.65, 080506.65, 080507.65 и 080105.65)
- •7.1.2. Разработка системы принятия решений об аттестации знаний абитуриента
- •Правила вывода
- •1) Общая схема решения
- •2) Разработка базы данных для системы принятия решений
- •3) Построение дерева принятия решений
- •4) Реализация системы принятия решений в электронной таблице
- •7.2. Финансовые вычисления в эт. Балансовая модель (Тема изучается только студентами спец. 080502.65, 080506.65, 080507.65 и 080105.65)
- •Пример 1
- •Введем в любую ячейку эт формулу
- •Пример 2
- •Пример 3
- •Пример 4
- •Пример 5
- •7.3. Оптимизация управленческих задач
- •1) Построение математической модели
- •2) Разработка эт с начальным планом решения
- •3) Улучшение (оптимизация) плана перевозок
- •Раздел 8. Технологии хранения и поиска информации в базах данных (бд)
- •В процессе работы с разделом Вам предстоит:
- •В. Создание базы данных.
- •8.1. Основные понятия. Модели данных
- •Иерархическая модель данных
- •8.2. Структурные элементы реляционных бд. Нормализация отношений и типы связей в бд
- •8.3. Создание базы данных
- •1) Отбор атрибутов, сведения о которых должны храниться в бд
- •2) Выбор системы управления базами данных (субд).
- •Раздел 9. Информационные системы и информационное общество
- •9.1. Информационные системы и их классификация
- •9.2. Информационное общество, его гуманитарные и правовые проблемы
- •9.3. Информатика и информатизация образования
- •Заключение
- •Технические и программные средства обеспечения дисциплины
- •3.4. Глоссарий (краткий словарь терминов)
- •3.5. Методические указания к выполнению лабораторных работ
- •4. Блок контроля освоения дисциплины
- •4.1. Общие указания
- •Блок тестов текущего контроля.
- •Блок тестов рубежного контроля.
- •Блок итогового контроля за первый семестр.
- •Блок итогового контроля за второй семестр.
- •4.2. Методические указания к выполнению курсовой работы
- •4.2.1. Предисловие
- •Правила вывода:
- •4.2.2.3. Разработка системы принятия решений о продаже акций предприятия
- •4.2.2.4. Разработка системы принятия решений о диагностике неисправности телевизора
- •3) Реализация системы принятия решения в электронной таблице (эт)
- •4.2.3. Оптимизация управленческих и экономических задач
- •4.2.3.1. Принципы решения задач оптимизации
- •4.2.3.2. Решение транспортной задачи
- •Определение возможных режимов работы
- •Определение возможного графика работы
- •Определение числа работников, выходящих на работу каждый день согласно данному графику
- •Определение целевой функции задачи
- •4.2.3.4. Задача планирования выпуска продукции
- •4.2.3.3. Задача о распределении ресурсов
- •4.2.3.6. Задача об оптимальном составе сплава
- •4.2.3.7. Задача о производстве красок
- •4.2.4. Проектирование баз данных (бд)
- •4.2.4.1. Основные понятия
- •4.2.4.3. Пример выполнения курсовой работы по проектированию баз данных
- •Приложение 1
- •1.3.3. Реализация балансовой модели в электронной таблице (эт)
- •2. Задания на контрольную работу
- •Варианты контрольного задания
- •Задание 2
- •4.4. Блок тренировочных тестов текущего контроля (по темам дисциплины) Тест № 1 (к теме 1.1. Раздел 1)
- •2. Чем различаются понятия информация и данные?
- •3. Что такое дискретизация информации?
- •4. Что понимается под кодированием информации?
- •Тест № 2 (к теме 1.2. Раздел 1)
- •Тест № 3 (к теме 2.1. Раздел 2)
- •Для каких целей служит оперативное запоминающее устройство?
- •Перечислите наиболее важные характеристики эвм.
- •Что такое открытая архитектура компьютера?
- •Что из себя представляет многопроцессорная архитектура эвм?
- •В чем особенность кэш-памяти?
- •Тест № 4 (к теме 2.2. Раздел 2)
- •Тест № 5 (к теме 3.1. Раздел 3)
- •Что такое сетевая ос?
- •Что такое многопользовательская ос?
- •Тест № 6 (к теме 3.2. Раздел 3)
- •2. Назовите функции программы-компилятора.
- •Перечислите основные классы системных программ.
- •Перечислите основные классы прикладных программ.
- •Что такое алгоритм?
- •Что такое машинный код?
- •Дайте характеристику языку программирования низкого уровня.
- •Тест № 7 (к теме 3.3. Раздел 3)
- •Тест № 8 ( к Разделу 4)
- •Тест № 9 (к Разделу 5)
- •Тест № 10 (к теме 6.1. Раздел 6)
- •Тест № 11 ( к теме 6.2. Раздел 6)
- •Тест № 12 (к теме 6.3. Раздел 6)
- •Тест № 13 (к Разделу 7)
- •Тест № 14 (к теме 8.1. Раздел 8)
- •Тест № 15 (к теме 8.2. Раздел 8)
- •Тест № 16 (к теме 8.3. Раздел 8)
- •Тест № 17 (к Разделу 9)
- •П равильные ответы на тренировочные тесты текущего контроля
- •Тест № 2 (к Разделу 2)
- •3. Принцип действия cd-rom основан
- •5. Для каких целей используется адаптер?
- •Тест № 3 (к Разделу 3)
- •Тест № 4 (к Разделу 4)
- •Тест № 5 (к Разделу 5)
- •1. Чтобы добавить к имеющимся в окне Word еще одну панель, следует выполнить:
- •2. Для чего предназначена команда Предварительный просмотр меню Файл?
- •3. Как выделить фрагмент текста редактируемого документа?
- •4. Какой кнопкой надо воспользоваться, чтобы выбрать стиль?
- •5. Какой кнопкой нужно воспользоваться, чтобы вызвать редактор формул?
- •6. Чтобы вставить в текстовый документ рисунок, нужно выполнить следующую команду:
- •Тест № 6 (к Разделу 6)
- •Копируем а4 в в4. Какие числа в ячейках a4 и b4?
- •10. Копируем c3 в d3. Какая формула в d3?
- •12. В ячейке в3 вычисляется значение переменной t по формуле:
- •13 Вычислить в программе Calc значение переменной z от переменной y, где y находится в ячейке d2, по формуле:
- •14. Чтобы перемножить две матрицы, находящиеся в диапазонах а1:с3 и d1:f3 Excel, а результат поместить в ячейки а5:с7, нужно выполнить команды:
- •15. Целевая ячейка в режиме Поиск решения может принимать значения?
- •Тест № 7 (к Разделу 8)
- •6. Определите тип поля «Стаж работы»
- •Правильные ответы на тренировочные тесты рубежного контроля
- •4.6. Блок итогового контроля за первый семестр
- •Вопросы для подготовки к зачету
- •I. Информатика и информационные технологии
- •II. Вычислительная техника. Программное обеспечение
- •III. Операционная система windows
- •52. Какие команды Главного меню следует выбрать, чтобы попасть в программу Проводник?
- •57. Что такое архивация файлов?
- •IV. Текстовые процессоры
- •13. Язык программирования Ассемблер – это
- •15. Чтобы присвоить документу Word новое имя, нужно выполнить следующие команды:
- •24. Какая кнопка служит для уменьшения разрядности чисел после запятой?
- •28. Копируем d3 в c4. Какая формула в c4?
- •29. Копируем c3 в c4. Какие числа в c3 и c4?
- •31. В ячейке d2 Excel вычисляется значение переменной z по формуле
- •32. Вычислить в Calc значение переменной y от переменной X, где X находится в ячейке f2,по формуле
- •35. Фирма планирует поместить в банк некоторую сумму на пять лет под 15 % годовых с ежеквартальным начислением с целью накопить
- •100 000 000 Долл. Какую сумму следует поместить в банк?
- •36. Предлагаются три инвестиционных проекта, которые характеризуются потоками предполагаемых платежей
- •Блок итогового контроля за второй семестр Вопросы для подготовки к экзамену
- •Содержание
- •Раздел 1. Информация и информатика………………………......25
- •Раздел 2. Вычислительная техника…………………………….31
- •Раздел 3. Программное обеспечение компьютеров………………...39
- •Раздел 4. Сетевые технологии обработки информации………..…48
- •Раздел 5. Создание текстовых и графических документов……....54
- •Раздел 6. Обработка данных средствами электронных
- •Раздел 7. Реализация в эт управленческих и экономических
- •Раздел 8. Технологии хранения и поиска информации
- •Раздел 9. Информационные системы и информационное
- •Учебно-методический комплекс
- •191186, Санкт-Петербург, ул. Миллионная, д.5
Приложение 1
Ф
Государственное образовательное учреждение высшего профессионального образования
Северо-Западный государственный заочный технический университет
Кафедра информатики
КУРСОВАЯ РАБОТА
по
ИНФОРМАТИКЕ
Тема: Системы принятия решения и оптимизации в электронных таблицах,
конструирование баз данных
Выполнил студент:
Институт:
Курс:
Специальность:
Шифр:
Проверил преподаватель:
Оценка:
Подпись преподавателя:
Дата:
Санкт-Петербург
2009
4 .3.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
.3.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
(для студентов спец. 080502.65, 080506.65, 080507.65 и 080105.65)
В контрольной работе студенты должны выполнить четыре задачи, связанные с финансовыми расчетами, оптимизацией управленческих решений и планированием выпуска продукции.
1. Методические указания к решению задач
1 .1.
Финансовые функции в электронных
таблицах
.1.
Финансовые функции в электронных
таблицах
Вопросы решения финансовых задач с использованием функций электронных таблиц рассмотрены в «Опорном конспекте», с.80-83
1.2. Решение задач оптимизации
Решение задач оптимизации рассмотрено в «Опорном конспекте», с.89-96 и в «Методических указаниях к выполнению курсовой работы», п. 4.2.3, с. 137-163.
 1.3. Задачи анализа и прогнозирования
1.3. Задачи анализа и прогнозирования
Рассмотрим задачу планирования производства на примере балансовой модели.
Экономическая система состоит их трех отраслей. Объемы производства каждой из отраслей за предыдущий период, текущее производственное потребление в отраслях, а также прогнозируемый конечный спрос продукции каждой из трех отраслей приведены в табл. 4.35.
Таблица 4.35
|
Отрасли |
Объемы производства отраслей |
Производственное потребление отраслей за предыдущий период |
Прогнози- руемый конечный спрос |
||
|
1 |
2 |
3 |
|||
|
1 2 3 |
600 1000 800 |
250 150 0 |
100 500 300 |
160 0 400 |
2000 2000 3000 |
Определить конечную продукцию каждой из отраслей за предыдущий период и план выпуска продукции в следующем периоде, считая, что технология производства не изменилась.
1 .3.1.
Математическая постановка задачи
.3.1.
Математическая постановка задачи
Для решения поставленной задачи можно использовать балансовую модель Леонтьева. Она представляет собой систему уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этой продукции. В рассматриваемой задаче экономическая система состоит из трех отраслей.
Пусть Хi - величина, равная суммарному выпуску продукции отрасли - i;
xij - количество продукции отрасли i, необходимой для того, чтобы отрасль j произвела Xj единиц своей продукции;
Yi - количество продукции отрасли i, остающееся после удовлетворения внутреннего спроса отраслей (конечная продукция).
Тогда взаимосвязь отраслей в процессе производства и потребления отдельного продукта Хi (i=1, 2, 3) может быть описана в виде следующих уравнений:
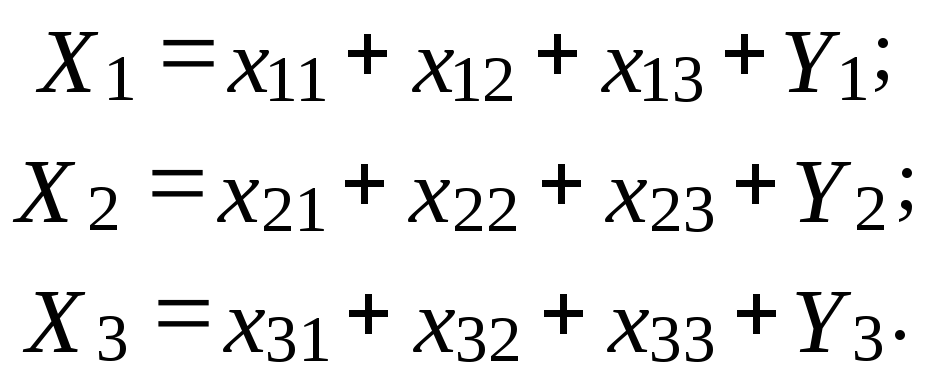 (4.24)
(4.24)
Используем понятие коэффициентов прямых затрат (технологического коэффициента) aij:
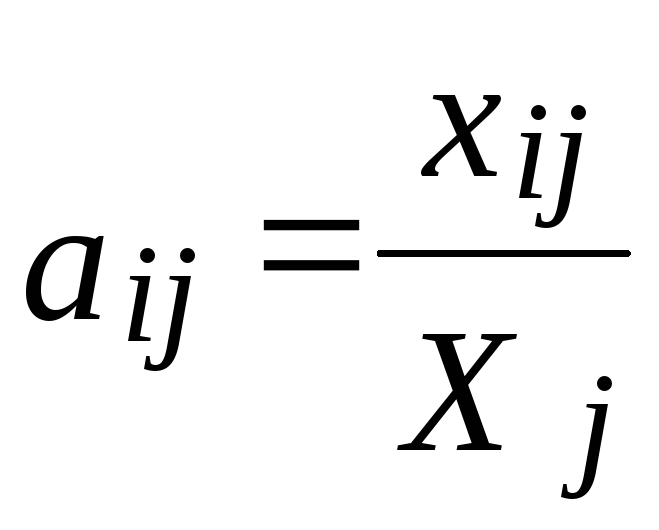 - количество продукции отрасли i,
необходимой для того, чтобы отрасль j
произвела одну единицу своей продукции.
- количество продукции отрасли i,
необходимой для того, чтобы отрасль j
произвела одну единицу своей продукции.
Тогда xij=aijXj и система уравнений (4.24) будет иметь следующий вид:
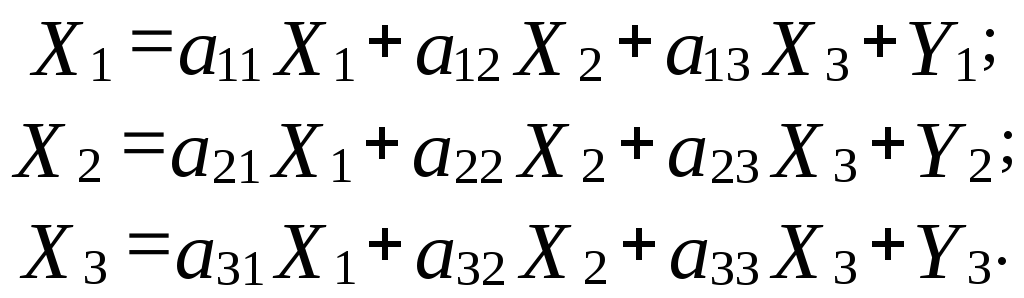 (4.25)
(4.25)
Или в матричной форме
X=AX+Y, (4.26)
где
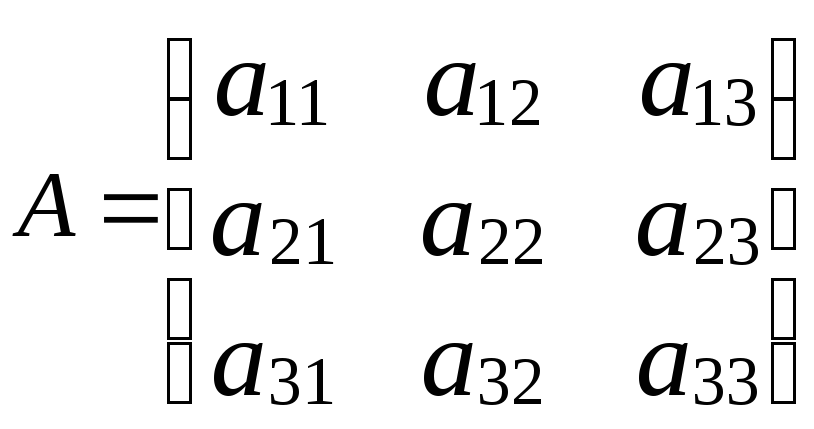 - матрица прямых затрат,
- матрица прямых затрат,
Х - вектор-столбец выпуска продукции в предыдущем периоде;
Y - вектор-столбец конечного спроса в предыдущем периоде.
1.3.2. Аналитическое решение задачи
О пределение
вектора конечной продукции за предыдущий
период
пределение
вектора конечной продукции за предыдущий
период
По условию задачи известны объемы производства каждой из отраслей за предыдущий период (суммарный выпуск продукции отрасли i): X1=600, X2=1000, X3= 800 и значения xij (i,j=1, 2, 3):
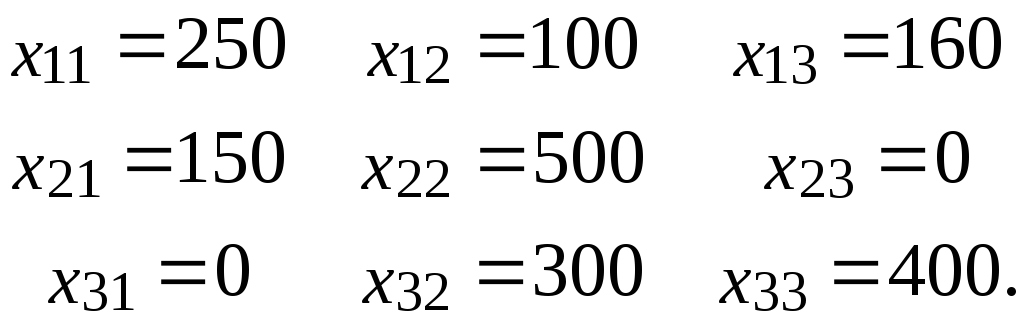
Отсюда, используя табл. 4.35, можно определить значения Yi, i=1, 2, 3 конечной продукции каждой из отраслей за предыдущий период.

Таким образом, вектор конечной продукции за предыдущий период найден: Y=(90, 350, 100).
Для определения вектора выпуска продукции Х при заданном конечном прогнозируемом векторе спроса Y=(2000, 2000, 3000) надо решить систему уравнений (4.26), из которой следует, что
![]() (4.27)
(4.27)
где Е - единичная матрица;
S=(E-A)-1 - называется матрицей полных затрат.
Определение коэффициентов прямых затрат
Учитывая, что технология производства не изменилась, определим коэффициенты прямых затрат aij:
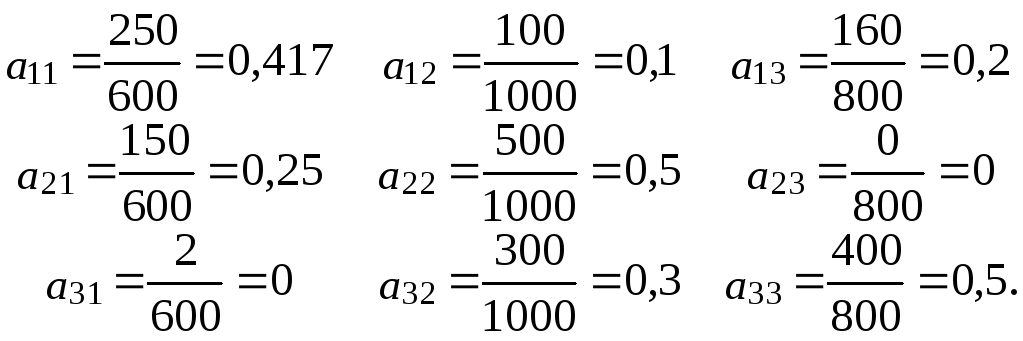
Таким образом, матрица коэффициентов прямых затрат будет иметь вид
 .
.
Проверка продуктивности матрицы
Все элементы матрицы А неотрицательные, А0.
Для того чтобы система уравнений (4.26) имела единственное неотрицательное решение при любом неотрицательном векторе Y, необходимо, чтобы матрица А была продуктивной. Экономический смысл продуктивности состоит в том, что существует такой план выпуска продукции, при котором каждая отрасль сможет произвести некоторое количество конечной продукции. Известно, что для продуктивности матрицы А0 необходимо и достаточно, чтобы все главные миноры матрицы (Е-А) были положительными числами, строго меньше единицы. Кроме того, если сумма элементов каждого из столбцов неотрицательной квадратной матрицы А положительна и строго меньше единицы, то все главные миноры матрицы (Е-А) положительны и строго меньше единицы.
Суммы элементов каждого столбца матрицы А соответственно равны
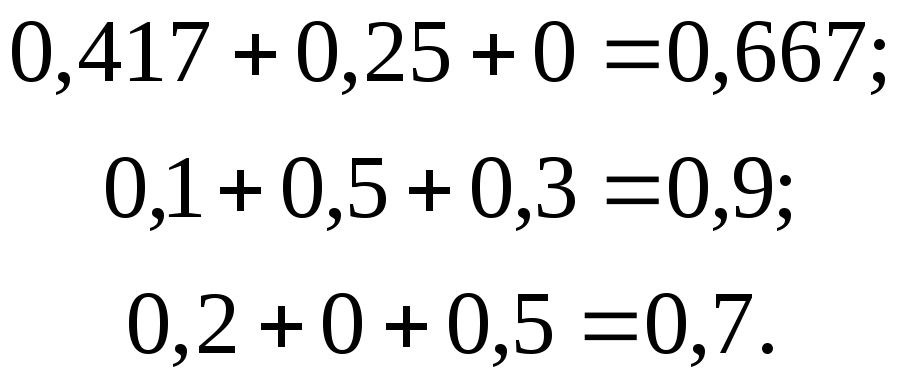
Следовательно, в силу вышесказанного, матрица А продуктивна, выражение (4.27) имеет смысл и вектор Y неотрицателен. Следовательно, для нахождения плана выпуска продукции Х можно воспользоваться формулой (4.27).
Вычисление матрицы Е-А
Вычислим матрицу (Е-А):

Вычисление обратной матрицы (Е-А)-1
Известно, что матрица В-1 называется обратной по отношению к квадратной матрице В, если произведение В*В-1=Е (Е - единичная матрица).
Для вычисления обратной матрицы воспользуемся формулой
![]() , (4.28)
, (4.28)
где [Bij] – матрица, полученная из элементов Bij, а Bij - алгебраические дополнения элементов i j матрицы.
Bij=(-1)i+j Mij, (4.29)
где Mi - минор элемента Bij (минор – это такой определитель, который получается из матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент).
Вычислим значения алгебраических дополнений элементов матрицы (Е-А). Обозначим для простоты описания вычислений Е-А=В:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Таким
образом,
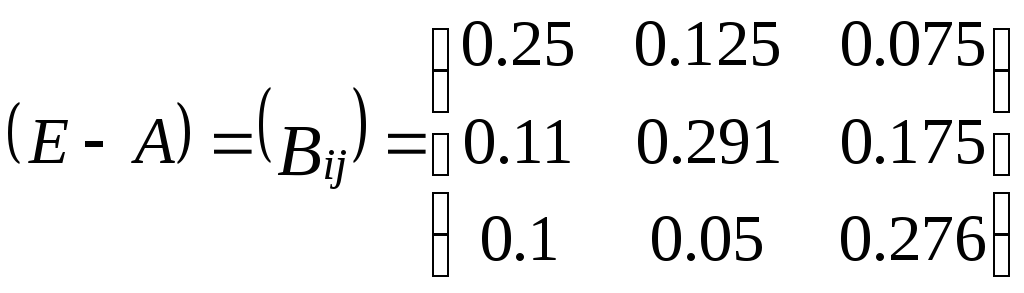 .
.
Вычисление транспонированной матрицы
Поменяв в матрице (Е-А) строки и столбцы местами, получаем
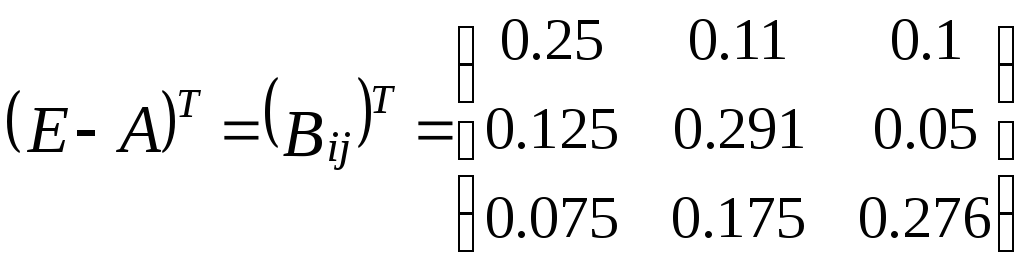
Вычисление определителя матрицы (Е-А)
Вычислим определитель, применив разложение по первой строке:
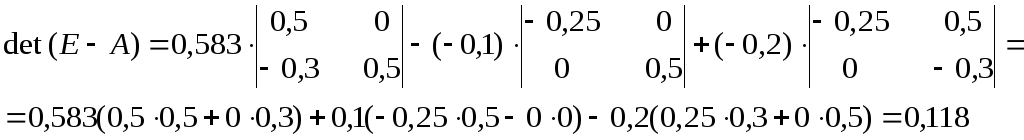
Вычисление матрицы прямых затрат S
По
формуле S=(E-A)-1=B-1=![]()

 .
.
Определение вектора выпуска продукции Х
Зная S и Y, вычислим X по формуле
 .
.
Отсюда
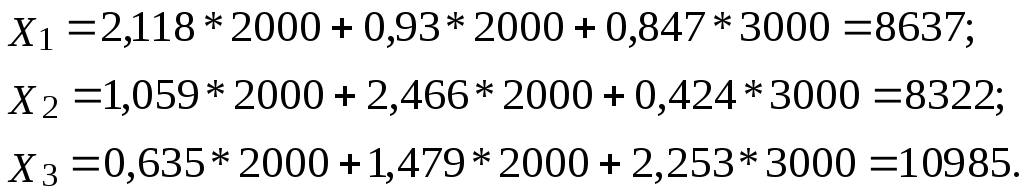
Таким образом, вектор выпуска продукции в следующем периоде при заданном векторе конечной продукции
Y=(2000, 2000, 3000) равен X=(8637, 8322, 10985).
Очевидно, что с использованием матричных операций в Excel процедура вычислений в балансовой модели существенно упрощается.
