2.2 Контур управления

Объект управления, который представляет собой последовательное соединение инерционного звена первого порядка и звена запаздывания, представлен в контуре в виде двух последовательно включенных инерционных звеньев первого порядка. Структурная схема объекта управления представлена на рисунке 2.2.

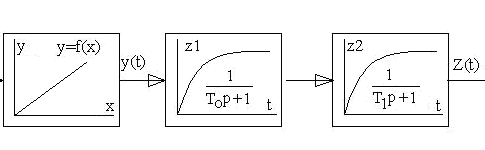
Рисунок 2.2 - Структурная схема объекта управления

Статические свойства объекта управления моделируются в виде функциональной зависимости Y=f(x), где Y-установившееся значение регулируемого параметра; x-значение входного параметра (положение выходного вала ИМ в процентах хода).

Инерционные свойства объекта с самовыравниванием идентифицируются апериодическим звеном первого порядка с передаточной функцией, представленное формулой (2.5):

W₁(p)=1/(T_op+1), (2.5)

где T₀ = 4 с.

Влияние звена запаздывания учитывается введением второго инерционного звена с передаточной функцией, представленное формулой (2.6):

W₂(p)=1/(T₁p+1), (2.6)

где T₁ = 0,8 с.

Структурная схема концентрацией водорода в защитном газе представлена на рисунке 2.3.

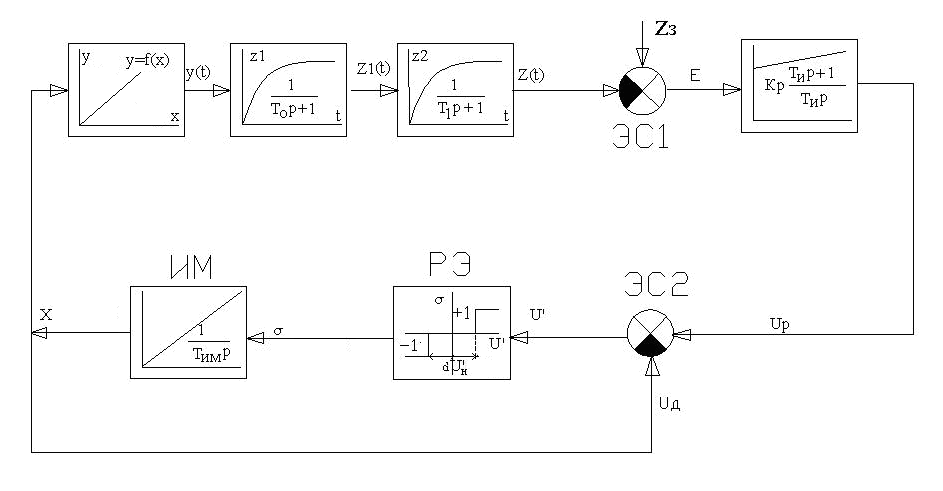
Рисунок 2.3 - Структурная схема моделируемого контура

Рассмотрим принцип действия системы регулирования. Текущее значение входной величины X подается на вход звена, имитирующего нелинейную статическую характеристику объекта управления (ОУ) затем на два звена, имитирующие инерционные свойства объекта. Сигнал с выхода объекта Z сравнивается с сигналом Z_З. Разница E=Z_З -Z с элемента сравнения ЭС1 поступает на вход ПИ-регулятора. ПИ-регулятор отрабатывает сигнал рассогласования Е во времени, вырабатывая на выходе управляющее воздействие U_Р, которое, после вычитания сигнала обратной связи Δx, подается на вход релейного элемента.

Релейный элемент представляет собой трехпозиционное реле, которое переключается в зависимости от уровня сигнала U’=U-X (где X=к_иt) и зоны нечувствительности

2.3 Расчет регулятора

2.3.1 Аппроксимация статической характеристики объекта

управления методом наименьших квадратов

Статическая характеристика реальных промышленных объектов управ­ления обычно получают, проводя специальный эксперимент на действующем объекте в реальных производственных условиях путем измерения выходного параметра объекта при некоторых дискретных значениях входного. Для математического описания экспериментальной статической характеристики используются регрессионные уравнения, представленное формулой (2.2), чаще всего предпочтение отдается многочленам целых положительных степеней:

(2.2)

где - ордината теоретической линии регрессии,- входной параметр.

В данном проекте использован метод наименьших квадратов.

Суть метода наименьших квадратов заключается в том, чтобы для всего интервала изменения аргумента выполнялось условие, представленное формулой (2.3):

, (2.3) (2.3)

где n- число экспериментальных пар;

Y_i - экспериментальное значение при Х=Х_i;

- ордината линии регрессии при Х=Х_i.

Так как вид статической характеристики не отличается от линейного, то степень аппроксимирующего многочлена возьму n=1.

Тогда аппроксимирующий многочлен будет иметь вид: y(x)=a+b^.x. Значение

коэффициентов a, b находим из решения системы уравнений, [15] представленное формулой (2.4):

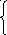 y_i = na + b  x_i;

 x_iy_i = a  x_i + b  x_i² (2.4)

Для решения системы (2.4) составлю таблицу 2.1.

Таблица 2.1 - Расчёт сумм для составления системы уравнений

№	Xi	Yi	Xi2	Xi*Yi
1	0	0	0	0
2	10	1,35	100	13,5
3	20	2,76	400	55,2
4	30	4,15	900	124,5
5	40	5,55	1600	222
6	50	6,95	2500	347,5
7	60	8,4	3600	504
8	70	9,7	4900	679
9	80	11,1	6400	888
10	90	12,5	8100	1125
11	100	13,9	10000	1390
∑	550	76,36	38500	5348,7

Коэффициенты линии регрессии находятся из определителей методом Крамера следующим образом:

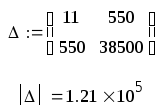
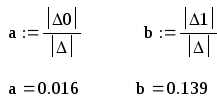
Искомое уравнение будет иметь вид:

Y(x) = 0,016 + 0,139x.

Статическая характеристика объекта управления представлена на

рисунке 2.1, где отмечены экспериментальные точки и линия регрессии, полученная в результате расчета.

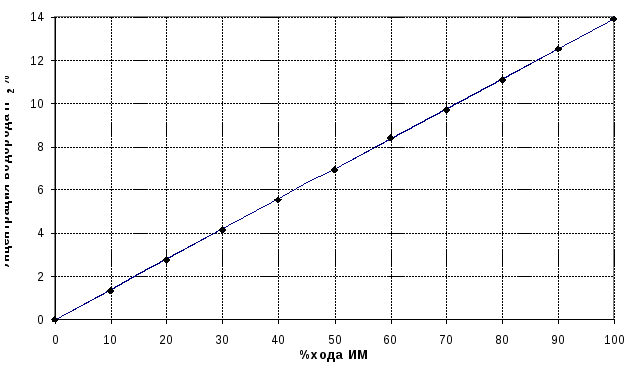
Рисунок 2.1 - Аппроксимация статической характеристики полиномом

1-ой степени