15 Графики символьных функций – команды ezplot, ezpolar

Чтобы избавить пользователя от хлопот, связанных с построением графиков функций с помощью стандартных средств (например, команды plot, [2]), в пакет Symbolic введены довольно удобные графические команды класса ezplot:

ezplot(f) – строит график символьно заданной функции f(x) независимой переменной x в интервале [- 2*pi;2*pi];

ezplot(f,xmin,xmax) – делает то же, но позволяет задать диапазон изменения независимой переменной x в интервале от xmin до xmax;

ezplot(f, [xmin, xmax, ymin, ymax]) – строит график функции f(x,у) = 0 для xmin < х < xmax, ymin < y < ymax.

Построим график функции sin(t)/t (рисунок 3):

>> ezplot('sin(t)/t'),grid

Рисунок 3

Следующая команда строит график гиперболы u² - v² - 1 = 0 для - 3 < u < 3, - 3 < v < 3 (рисунок 4):

>> ezplot('u^2-v^2-1',[-3, 3, -3, 3]),grid

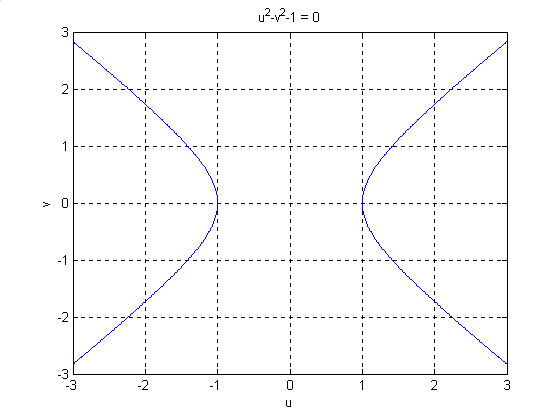
Рисунок 4

Ранее с помощью команды ezplot был построен график на рисунке 2.

График функции f(t) в полярной системе координат строит команда ezpolar:

ezpolar(f) – строит график функции f(t) при изменении угла t от 0 до 2π;

ezpolar(f,[a b]) – строит график функции f(t) при изменении угла t от a до b.

Построим график функции cos3t в полярной системе координат (рисунок 5):

>> ezpolar('cos(3*t)')

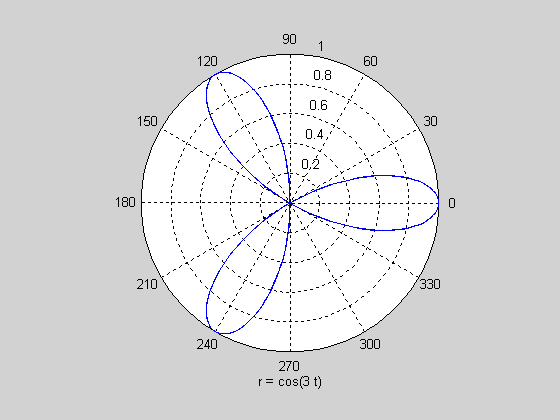
Рисунок 5

Помимо команд ezplot и ezpolar, пакет Symbolic поддерживает построение графиков других типов. Так, команда ezcontour служит для построения контурных графиков функций вида f(x,y). Похожая команда ezcontourf строит контурные графики с функциональной окраской областей между линиями равного уровня. Для построения трехмерных графиков параметрически заданных функций служит команда ezplot3. Команды ezsurf, ezsurfc, ezmesh, ezmeshc применяются для построения графиков поверхностей, заданных функциями двух переменных f(x,y). Справку с примерами по применению любой из этих команд можно получить с помощью команды doc <имя команды>.

16 Прямой доступ к ядру системы Maple – команда maple

Применение возможностей системы Maple совместно с возможностями системы MATLAB придает последней особую гибкость и резко расширяет возможности решения сложных математических задач, где целесообразно объединять аналитические (символьные) методы с численными расчетами.

Доступ к большинству функций и команд системы Maple, ядро которой включено в МАТLAB, осуществляется командой maple.

Пример:

Найти аналитическое решение дифференциального уравнения y''+2xy'+ny = 0.

Решение:

Обращение к dsolve приводит к решению, выраженному через функции Уиттекера:

>> dsolve('D2y+2*x*Dy+n*y=0','x')

ans =

C1/x^(1/2)*WhittakerW(1/4*n-1/4,1/4,x^2)*exp(-1/2*x^2)+C2/x^(1/2)*WhittakerM(1/4*n-1/4,1/4,x^2)*exp(-1/2*x^2)

Непосредственно из МАТLAB функции WhittakerW и WhittakerM недоступны, т.к. их нет в списке mfunlist функций системы Maple, доступных из МАТLAB [2].

Определение функций функций Уиттекера, варианты вызова и подробное описание с примерами использования возвращает команда mhelp Whittaker. Вычислим значение одной из них:

>> maple('WhittakerM(1,2,3)')

ans =

WhittakerM(1,2,3)

>> vpa(ans,7)

ans =

10.17605

Ниже приводятся примеры решения в МАТLAB некоторых математических задач с привлечением возможностей системы Maple.