Теоретические основы электротехники-2

Глава 12. Расчет электрических цепей при воздействии импульсных ЭДС 133

накопленной в реактивных элементах цепи энергией. Вторая составляющая отражает принужденную реакцию цепи на воздействие источников ЭДС и токов.

и предложить еще один способ расчета переходного процесса в сложных цепях. Поскольку переменные состояния должны удовлетворять начальным условиям xk(–0) xk(+0), то можно записать

т. е. получить общее решение матричного дифференциального уравнения в форме, исключающей операцию интегрирования.

Важным преимуществом такого способа решения системы дифференциальных уравнений является возможность исключения процедуры пошагового интегрирования и использования широкого спектра воздействующих функций в виде таблиц изображений Fk(p, t). Для расчета переходного процесса по этому методу следует предварительно рассчитать изображения функций, определяющих ЭДС и токи. Именно предварительно рассчитанные при помощи правого преобразования Лапласа изображения являются основой данной методики. Для расчета переходного процесса в конкретной цепи следует лишь составить матрицу À параметров уравнения состояний данной цепи и, заменив оператор ð в изображени Fk(p, t) íà –À, определить установившееся значение функции x k (t) B k Fk ( A, t). При такой замене для искомых переменных состояния происходит переход от ординарных функций времени к матричным.

Расчет переходных процессов, также как и установившихся режимов, сложных электрических цепей, как правило, производится при помощи ЭВМ с большим пакетом стандартных программ, в том числе и с программами, оперирующими матричными функциями. По этой причине переход от пошагового интегрирования для расчета установившегося режима к операциям с матричными функциями является большим преимуществом. Это преимущество становится решающим в задачах, где целью пошагового интегрирования уравнения (*) является выход на установившийся режим.

В описанной методике решения системы линейных дифференциальных уравнений состояния электрических цепей (а также иных систем с аналогичными уравнениями) важное место, помимо операций с функциями от матриц Fk(–À, t), занимает вычисление матричной экспоненты eAt . Суть проблемы заключается

134 Часть 2. Теория линейных электрических цепей

в том, что непосредственное вычисление eAt при помощи разложения eAt â ðÿä,

как по мере роста t необходимо увеличивать количество слагаемых для сохранения требуемой точности расчета. По этой причине важнейшим требованием организации процесса численного расчета матричной экспоненты является со- четание точности расчета с эффективностью процесса вычисления. В случае матрицы À с очень малыми собственными значениями, соответствующими большим постоянным времени, повышение точности приводит к увеличению времени расчета. Действительно, можно подобрать такой временной шаг h, ïðè êî-

количестве слагаемых ряда. Однако такой шаг интегрирования в выражении (*) и при вычислении eAt приведет к нежелательному и в большинстве случае неприемлемому удлинению времени расчета.

Изящный метод решения (*), уже использовавшийся в § 9.17, предложил Ю. В. Ракитский. В части вычисления eAt он заключается в последовательном удвоении начального шага h до значительно большего шага H h2N , при котором решение достигается за приемлемое время. Для этой цели им предложены формулы, позволяющие выполнить последовательное увеличение шага h äî çíà-

стоящих из операции умножения матриц, можно найти значение матрицы eAH !N eAh2N . Определив eAH легко использовать те же реккурентные соот-

ношения для последовательного вычисления eAt в желаемые моменты времени, кратные H.

12.6. Расчет электрических цепей при воздействии импульсных ЭДС методом правого преобразования Лапласа

В §§ 9.10 и 12.2 рассмотрены некоторые особенности процессов в электрических цепях с бесконечно большими импульсными токами и напряжениями. Там же было указано, что такие токи и напряжения появляются в результате физически нереализуемых допущений, например мгновенного характера процесса коммутации, пренебрежения индуктивностями и емкостями отдельных элементов и участков электрической цепи. Такого рода допущения в некоторых случаях позволяют упростить задачу расчета цепей и нередко используются на практике. Рассмотрим особенности расчета цепей, для которых характерно наличие в них бесконечных, т. е. в количественном отношении неопределенных токов и напряжений. Неопределенность амплитудых значений импульсов заставляет оперировать со связанными с ними определенными характеристиками.

Импульсные токи и ЭДС количественно однозначно могут быть характеризованы величинами их площадей. Площадь импульса тока конечна и равна инте-

гралу 0 t idt i( ) t( 0) и однозначно определяет количество связанного с

этим импульсом заряда Q. В замкнутом контуре, содержащем резисторы и конденсаторы, прохождение импульса тока через конденсатор изменяет его заряд на конечную величину i( ) t( 0) Q. В замкнутом контуре, состоящем из резисторов и индуктивных катушек, импульс ЭДС однозначно определяет изменение потокосцепления < контура, т. е. суммы потокосцеплений индуктивных катушек, на конечную величину e( ) t( 0) <. Согласно фарадеевской формулировке закона электромагнитной индукции (см. § 1.10) < r Q, импульс ЭДС в замкнутом контуре приводит к появлению импульса тока, зависящего от сопротивления r контура. Следовательно, расчет цепей с импульсными источниками тока и ЭДС сводится к нахождению распределения площадей импульсных токов и напряжений ветвей цепи. В резистивных цепях токи и напряжения ветвей можно рассчитать при помощи известных методов расчета цепей имея в виду, что они однозначно характеризуются их конечными площадями. Для резистивных цепей токи и напряжения в цепи равны нулю во всем интервале времени, кроме интервалов t( 0) воздействия импульсных ЭДС и токов.

В цепях с индуктивными катушками и конденсаторами импульсные токи и напряжения скачкообразно на конечную величину меняют токи индуктивных катушек и напряжения конденсаторов. Эти изменения происходят в первой, длящейся в течение времени t( 0), импульсной фазе процесса. Этот процесс приводит также к скачкообразному изменению энергии магнитного поля индуктивных катушек и электрического поля конденсаторов. Спустя время t( 0) наступает вторая фаза процесса, в течение которой участки цепи с источниками импульсных ЭДС оказываются как бы короткозамкнутыми, поскольку на этих участках ЭДС и, соответственно, падение напряжения равны нулю, а участки цепи с импульсными источниками тока — разомкнутыми, поскольку токи в них равны нулю. Во второй фазе импульсные ЭДС и токи равны нулю и процесс в цепи поддерживается скачкообразно появившейся после первой фазы энергией магнитных полей индуктивных катушек и электрических полей конденсаторов. Эта энергия определяет матрицу начальных значений переменных состояний цепи x(0), а также свободные токи и напряжения матрицы x(t). При наличии резистивных элементов процесс в цепи носит затухающий характер и свободные токи и напряжения могут быть рассчитаны по формуле x(t) [exp(At)]·x(0). Сказанное относилось к случаю одиночного импульса. Если импульсы источников ЭДС и токов повторяются во времени по некоторому закону, то такой процесс может быть рассчитан при помощи правого преобразования Лапласа.

Расчет процессов в цепях с источниками импульсных ЭДС и токов в общем случае, в свете изложенного в § 12.5, также сводится только к нахождению изображения воздействующей на цепь импульсной функции. В качестве примера рассмотрим расчет установившегося режима в цепи r, C при воздействии ЭДС в виде знакопеременных импульсов, отстоящих друг от друга на интервал Ò/2. Такая функция может быть представлена в виде

f (t)−(t) f (t)[−(t ) −(t T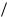2)],

136 Часть 2. Теория линейных электрических цепей

ãäå f(t) — некоторая функция определяющая площадь импульса, −(t) — единич- ная импульсная функция с площадью равной единице, t t 2E(t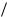2), à E(t/2) — целая часть аргумента t/2.

Правое преобразование Лапласа −(t) в первом интервале 0 – Ò/2 имеет вид(p, t) e pt [1 1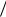(1 epT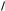2 )].

Вычислим установившееся значение напряжения на конденсаторе в цепи r, C, для которой уравнение состояния имеет вид

duC /dt ÀuC + Âu(t) –uC /rC + u(t)/rC.

Для определения U(p, t) следует принимать во внимание, что (p, t) является изображением импульсной функции с Ê Å t 1 (см. § 12.2). Для перехода от(p, t) к изображению функции u(t) необходимо либо заранее задать значение площади импульса, либо определить еe при помощи дополнительных условий. Пусть после прохождения импульса тока бесконечной величины конденсатор заряжается до значения U0. Определим соответствующую этому условию площадь импульсной функции f(t)−(t). Эта площадь равна U x t (U x è

t 0). В течение промежутка времени t 0 по конденсатору протекает ток

U x 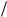r i , приводящий к скачкообразному росту заряда конденсатора на величину Q. Имеет место равенство U x t tU x r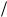r tir. Учитывая равенство Q ti U 0C можно определить площадь импульса U x t U 0 rC. Тогда U(ð, t)

1 e2rC

Нетрудно заметить, что решение для u (t) в первом полупериоде может быть

C

использовано для расчета процесса при воздействии одиночного импульса. Для

этого достаточно в выражение для u (t) подставить T , и тогда

C

u (t) U exp( t rC).

C 0

Решение этой простейшей задачи можно получить и при помощи следующих соображений. В установившемся режиме при положительном импульсе u(t) íà-

пряжение на конденсаторе u (t) скачкообразно меняется на величину U îò íå-

C 0

которого значения –U1 äî U2, а при отрицательном импульсе — от U1 äî –U2.

Затем в процессе разряда, когда ЭДС равна нулю (цепь на входных зажимах как бы короткозамкнута), напряжение U2 уменьшается по закону U 2 e t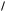rC до значе- ния U1 U 2 e T2rC . Поскольку U2 + U1 U0, то имеет место равенство

U1 (U0 – U1)e T2rC

èëè U1(1 eT2rC ) U 0 . Тогда в интервале 0 < t < T/2

1 e2rC

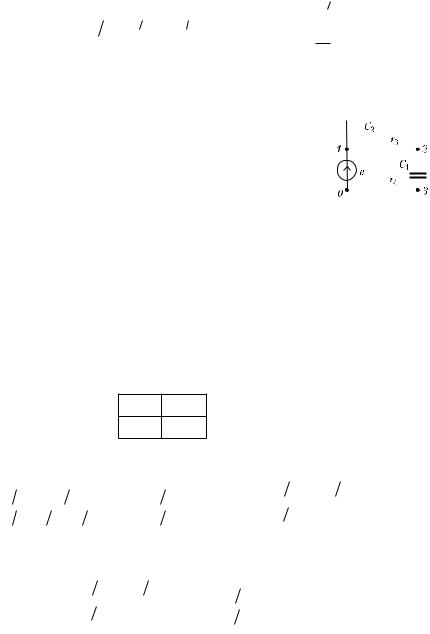
В качестве более сложного примера рассмотрим процессы в цепи с двумя конденсаторами (рис. 12.10). Матрица соединений A этой цепи имеет вид(см. § 9.12)

Матрица контурных соединений F для двух контуров, образованных двумя ветвями связи (ветвь 3 с резистором r3 и ветвь 4 с резистором r4), имеет вид

Согласно приведенным в § 9.13 формулам, для FGC можно записать

–1

1 1

Для остальных матриц имеем: FGÅ | 0,1| t, R diag(r3, r4), C diag(C1, C2),

Произведя все матричные операции для напряжений двух накопителей энергии u1 è u2, можно записать уравнения состояний

138 Часть 2. Теория линейных электрических цепей

èëè

В данном случае также возникает необходимость введения дополнительного условия для вычисления изображения U(p, t) по известному (p, t). Наличие пути для бесконечного импульса тока по двум конденсаторам через резистор r4 приводит к скачкообразному росту их зарядов на величину Q. При этом скачкообразно изменяются также напряжения u1 è u2 конденсаторов. В качестве дополнительного условия примем, что после прохождения импульса тока суммарное напряжение равно u2(+0)+ u1(+0) U0. Воспользуемся тем, что скачки напряжений u2 è u1 конденсаторов обратно пропорциональны емкостям конденсаторов. При этих условиях заряд Q U0Cý U0 /(1/C1+1/C2) U0C1C2 /(C1+C2). Следовательно, аналогично примеру простой цепи, (p, t) следует умножать на U0 è íà r4Cý (ãäå Cý C1C2/(C1 +C2)). При этих условиях U(ð, t) равно

U(ð, t) p, t)U0/(1/r4C1 + 1/r4C2) p, t)U0 r4C1C2 /(C1 + C2).

Соответственно решение для установившегося режима при воздействии ЭДС в форме периодических знакопеременных импульсов будет иметь вид

u (A, t) e At [1 1(1 eAT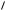2 )]BU 0 r4C1 C2 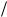(C1 C2 ).

Нетрудно заметить, что площадь импульса U0 r4C1C2 /(C1 + C2) формально можно вычислить по матрице Â. Она обратна сумме тех строк Â, которые входят в контур, образованный конденсаторами C1 è C2. В данном случае в контур входят обе строки и площадь равна U0 /(1/r4C1 + 1/r4C2) U0 r4Cý.

Энергетические процессы в цепях с импульсными ЭДС и токами, с точки зрения эффективности использования электромагнитной энергии, требуют особого рассмотрения. В § 12.2 при исследовании процесса зарядки конденсатора в цепи rC показано, что потери энергии и КПД ее использования впрямую зависят от скорости накачки энергии в электрическое поле конденсатора. Только при бесконечно медленном приращении напряжения на зажимах конденсатора удается всю энергию источника перевести в электрическое поле конденсатора. При скач- кообразном приложении постоянного напряжения к цепи r, C половина энергии источника теряется и КПД процесса зарядки оказывается равным 0,5. В цепях с импульсными токами и напряжениями, где изменения напряжений и токов в процессе зарядки могут быть теоретически бесконечно большими, следует ожидать еще больших потерь энергии и еще более низких КПД использования энергии.

Например, чтобы в цепи r, C за очень малое время t напряжение на конденсаторе выросло, скажем, от нуля до величины U0 при конечной постоянной времени rC, необходимо будет приложить такое напряжение, при котором Uõ(1 – e– t/ ) U0. При условии t << , Uõ должно быть больше U0 â 1/(1 – e– t/ ) раза. Учитывая условие t << и разложив e– t/ â ðÿä, Uõ приближенно можно

Глава 12. Расчет электрических цепей при воздействии импульсных ЭДС 139

представить в видеU x U 0 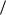(1 (1 t 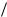)) U 0 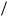t. Если, например, rC 1 мс и длительность импульса t 0,0001 rC, òîU x U 0 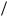t 10000U 0 . Потери энергии в виде выделяющегося в резисторе тепла приближенно можно рассчитать следующим образом. Для расчета тока в интервале 0 ... t воспользуемся условиями t << è Uõ >> U0. Тогда для приближенной оценки с достаточной точ- ностью можно полагать i U x 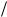r, и потери энергии за время t будут равны

P t tU x2 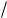r. Отношение à потерь энергии к энергии, накопленной в конденсаторе, будет равно

и для случая с 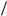t 10000 полезная энергия, накопленная в конденсаторе, оказывается много меньше потерь энергии. Низкие значения КПД цепей с импульсными токами и напряжениями следует учитывать при использовании таких цепей в системах преобразования энергии, где эффективность ее использования является важным критерием выбора того или иного технического решения.

Приведенные примеры показывают возможности и сложности применения метода правого преобразования Лапласа для расчета установившихся режимов при импульсных воздействиях. Еще раз отметим главную особенность данного метода, а именно перевод основной сложности расчета цепи на этап поиска изображения воздействующей на цепь импульсной функции. Наличие не зависящего от конкретной задачи изображения позволяет перейти к расчету конкретной и любой иной цепи при помощи простой операции замены оператора ð в изображении на матрицу параметров уравнения состояния данной цепи и умножении этой матричной функции Fk(–À, t) íà Âk.

12.7. Расчет цепи при действии последовательности импульсов путем решения разностных уравнений цепи

В ряде практических задач, например при передаче цифровых сигналов, достаточно определить значения искомой реакции цепи только в дискретные моменты времени t 0, T, 2T, …, nT. В этом случае информация о реакции цепи внутри интервала повторяемости импульсов может быть получена с использованием дискретных значений в качестве начальных условий. Такие задачи характерны для современных систем связи, управления и переработки данных, когда передаваемая информация представлена последовательностью импульсов. Последовательность импульсов можно характеризовать периодом T их следования

èдлительностью импульса Òè. В пределах времени действия импульса форма

èамплитуда отдельных импульсов могут отличаться друг от друга.

Расчет цепи при действии последовательности импульсов может быть выполнен операторным методом, а также с помощью интеграла Дюамеля. При использовании операторного метода основная трудность заключаются в полу- чении операторного изображения последовательности импульсов. Применение интеграла Дюамеля к последовательности различных импульсов также приводит к громоздкой процедуре вычислений.

140 Часть 2. Теория линейных электрических цепей

Поэтому для расчета цепей при действии последовательности импульсов были разработаны специальные методы, которые позволяют определить значе- ния тока или напряжения в цепи (реакцию цепи) в дискретные моменты времени, совпадающие с началом действия каждого импульса. Будем предполагать, что длительность Òè импульса мала в сравнении с интервалом времени, которое необходимо анализируемой цепи для выхода на установившийся режим. Последовательность импульсов может быть описана аналитически с помощью единичной функции 1(t) или c использованием −-функции. Например, последовательность прямоугольных импульсов c амплитудамиU n {U 0 ,U1,U 2 , } и длительностью Òè можно записать в виде следующей суммы:

n

u(t) U n 1(t nT) 1(t nT Tè ) .

n 0

Если длительность Òè импульса мала по сравнению с периодом Ò следования импульсов, то рассматриваемую последовательность можно описать с помощью −-функции. Действительно, полагая Òè 0 и переходя в последнем выражении к пределу при неизменной площади K n U nTè n-го импульса, имеем

откуда получим описание последовательности импульсов с помощью −-ôóíê- öèè

n

u(t) K n−(t nT).

n 0

Последовательности Un è Kn можно рассматривать как функции дискретного аргумента U n U(nT) U[n], K n K(nT) K[n] или решетчатые функции. Квадратные скобки здесь и далее показывают, что заключенная в них переменная принимает только положительные целочисленные значения. Решетчатая функция с заданным периодом T может быть построена для любой функции времени f(t) как последовательность дискретных значений функции f в моменты времени 0, T, 2T, Ο .

Можно провести аналогию между методами расчета цепей при воздействии непрерывных сигналов и методами расчета цепей при воздействии последовательности импульсов. При этом методам, основанным на решении дифференциальных уравнений при действии непрерывных сигналов, соответствуют методы, основанные на решении разностных уравнений при воздействии импульсов. Преобразованию Лапласа для непрерывных сигналов соответствует так называемое дискретное преобразование Лапласа или z-преобразование для дискретных функций, рассматриваемое в следующих параграфах настоящей главы.

Рассмотрим методы формирования и решения разностных уравнений цепи. Рассчитаем ток в цепи, изображенной на рис.12.11, при действии на ее входе прямоугольных импульсов постоянной амплитудой U0, с периодом следования Ò и длительностью Òè. Составим разностное уравнение для тока в цепи, которое для цепи первого порядка представляет собой рекуррентное соотношение, уста-

навливающее связь между значением тока в начале (n + 1)-го интервала со зна- чением тока в начале n-го интервала.

Ðèñ. 12.11

Ток в цепи на интервале nT t (n+1)T описывается дифференциальным уравнением L dtdi ri u(t), ãäå u(t) U 0 во время действия импульса и u(t)=0

в промежутке времени между импульсами. Будем отсчитывать время t t nT от момента начала действия n-го импульса. Решение в интервале времени 0 t T можно записать в виде i(t ) i (t ) Ae t (здесь & L/r — постоянная

времени цепи). Тогда i(t ) t 0 i(t) t nT и, соответственно, i(0) i[n]. Выразим постоянную A через значение тока в начале действия импульса и значение тока в установившемся режиме i (t ). На интервале 0 t Tè имеем i (t ) U 0 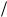r, и решение можно записать в виде

i(t ) U 0 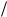r (i[n] U 0 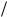r)e t .

На интервале Tè t T имеем i (t ) 0, в результате решение на этом интервале получаем из соотношения

Принимая в последнем уравнении t T, получим искомое рекуррентное соотношение:

Рекуррентное соотношение (*) представляет собой линейное разностное уравнение первого порядка с постоянными коэффициентами и позволяет рас- считать, начиная с i[1], последовательность дискретных значений тока в цепи:

i[1] i[0] q, i[2] 2 i[0] q(1 e T ), i[3] 3 i[0] q(1 e T e 2T ), ....

Òàê êàê i[0]=0, то получаемая последовательность представляет собой геомет-

142 Часть 2. Теория линейных электрических цепей

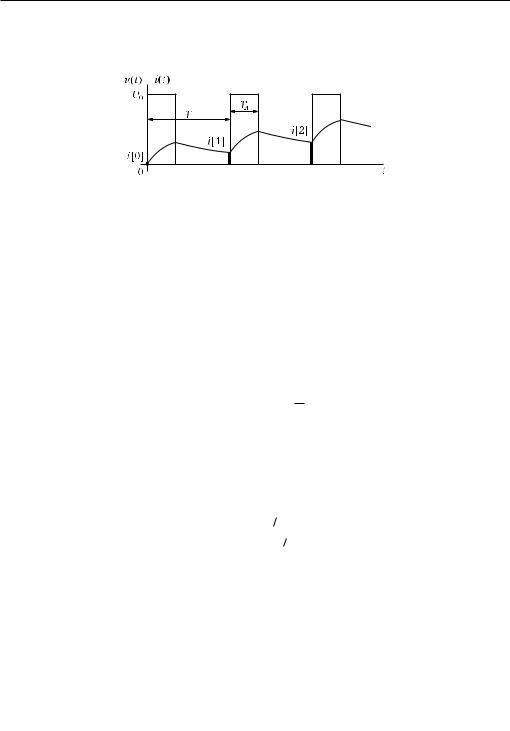
Последнее соотношение для тока i[n] представляет собой решения разностного уравнения (*). Решетчатая функция i[n] изображена на рис. 12.12 утолщенными вертикальными линиями.

Ðèñ. 12.12

Аналитические решения разностных уравнений для последовательностей импульсов можно получать также и другим способом, схожим со способом полу- чения решения дифференциального уравнения. Решение линейного разностного уравнения может быть представлено в виде

i[n] i [n] i [n],

ãäå i [n] — частное решение неоднородного разностного уравнения (*), а i [n] CΧn — общее решение однородного разностного уравнения i[n 1] i[n] 0. Как и для дифференциальных уравнений однородному разностному уравнению соответствует характеристическое уравнение Χ 0. Таким образом, решение разностного уравнения (*) имеет вид:

nT

i[n] i [n] Ce .

Обе составляющие решения должны быть определены таким образом, чтобы выполнялись условия при t 0 è ïðè t . Ïðè t i [n 1] i [n], поэтому при t в разностное уравнение (*) можно подставить i [n 1] i [n] и определить i [n] q(1 e T ). Коэффициент Ñ определим из начальных условий i[0] 0 i [n] C. В результате получим:

что совпадает с найденным ранее решением (**).

Рассчитаем далее значение тока в цепи на всем интервале повторяемости импульсов, используя полученные выражения для i[n]. Поскольку на интервале действия импульса приложенное напряжение постоянно, то для nT t nT + Òè имеем:

à äëÿ nT + Òè t (n + 1)Ò можно записать: