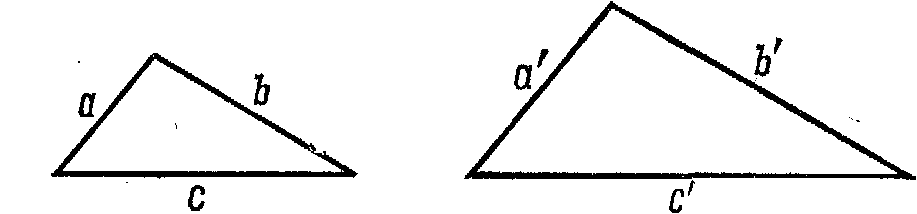Часть III структура пространства

 

 

Г лава 13 ПОСТУЛАТ ЕВКЛИДА О ПАРАЛЛЕЛЬНЫХ

Природа геометрии в физике представляет тему, имеющую большое значение для философии науки, – тему, между прочим, к которой я питаю специальный интерес. Я написал по этому предмету свою докторскую диссертацию и, хотя с тех пор мало опубликовал на эту тему, над ней я продолжаю много думать.

Почему эта тема так важна? Прежде всего она при­водит к анализу пространственно-временной системы, являющейся базисной структурой современной физики. Кроме того, математическая и физическая геометрии яв­ляются превосходными образцами двух фундаментально различных способов приобретения знания: априорного и эмпирического^23[1]. Если мы ясно поймем отличие между этими геометриями, то мы получим ценное понимание важных методологических проблем теории познания.

Рассмотрим сначала природу математической геомет­рии. Мы знаем, конечно, что геометрия была одной из самых ранних математических систем, которые были разработаны. Мы мало знаем о ее происхождении. Изу­мительным является то обстоятельство, что уже ко вре­мени Евклида она была так хорошо систематизирована. Аксиоматический характер евклидовой геометрии –

181

выведение теорем из фундаментальных аксиом и посту­латов – сам по себе был замечательным научным вкла­дом, который все еще продолжает играть основную роль в большинстве современных способов представления ма­тематических систем в точной форме. Удивительно, что этой процедуре уже следовали во времена Евклида.

Одна из аксиом Евклида, аксиома о параллельных, причиняла много беспокойства математикам в течение многих столетий. Мы можем сформулировать эту аксио­му следующим образом. На любой плоскости, на кото­рой имеется прямая Lи точкаPвне этой прямойL, существует одна и только одна прямаяL'на этой плоскости, проходящая черезP и параллельнаяL.(Две прямые на плоскости называются параллельными, если они не имеют ни одной общей точки.)

Эта аксиома казалась столь очевидной, что вплоть до начала прошлого столетия никто не сомневался в ее истинности. Споры, которые происходили вокруг нее, ка­сались не ее истинности, а того, является ли она необхо­димой в качестве аксиомы.Она казалась менее простой, чем другие аксиомы Евклида. Многие математики вери­ли, что она может статьтеоремой,которую можно будет вывести из других аксиом.

Были предприняты многочисленные попытки вывести аксиому о параллельных из других аксиом, и некоторые математики даже заявляли, что они добились здесь успе­ха. Мы знаем сегодня, что они ошибались. В то время не легко было увидеть ошибку в каждом из этих пред­полагаемых выводов, потому что они основывались – как это часто все еще делается в учебниках по геометрии для средней школы – на обращении к нашей интуиции. Мы делаем чертеж. По общему признанию, чертеж является неточным. Не существует никаких совершенных линий – линии, которые мы чертим, имеют толщину, по­тому что они проводятся на классной доске мелом или на бумаге чернилами, – но чертеж имеет целью воздействовать на наше воображение. Он помогает нам «ви­деть» истину, которую мы хотим доказать. Философия такого интуитивного подхода была наилучшим образом систематизирована Иммануилом Кантом. Интуиция является не нашим чувственным впечатлением от физиче­ского чертежа, а скорее нашим внутренним узрением геометрических конфигураций, которое не может быть

182

 

ошибочным. Позиция Канта здесь совершенно ясна. Никогда нельзя быть уверенным в том, что два отрезка прямой на классной доске являются равными, или в том, что меловая линия, изображающая круг, представляет действительный круг. Кант рассматривает такие чертежи только в качестве вторичного психологического фактора, чтобы помочь нам. Но он считал, что наша сила вообра­жения – то, что он называет Anschauung^24[2], интуиция, – является безошибочной. Если мы видим ясно геометри­ческую истину в уме, а не только нашими глазами, тогда мы видим ее с полной достоверностью.

Как мы постигаем, согласно Канту, утверждение, что две прямые не могут иметь больше одной общей точки? Мы представляем ситуацию мысленно. Вот две линии, которые пересекаются в одной точке. Могут ли они пересекаться где-то еще? Очевидно, не могут, потому что линии расходятся все больше и больше по мере того, как мы удаляемся от точки их пересечения. Кажется, таким образом, совершенно ясным, что две прямые либо имеют все точки общие (в таком случае они совпадают, чтобы образовать отдельную линию), либо они имеют самое большее одну общую точку, либо ни одной общей точки. Эти простые истины геометрии, считал Кант, мы усматриваемнепосредственно. Мы постигаем их истинность интуитивно. Тот факт, что мы не должны опираться на чертежи, привел Канта к предположению, что мы можем иметь полное доверие к истинам, полученным таким интуитивным путем. Позже мы вернемся к этой точке зрения. Здесь же мы упоминаем о ней только потому, что хотим помочь читателю понять способ мышления ученых начала девятнадцатого столетия в геометрии. Даже если они никогда не читали Канта, они имели ту же самую точку зрения^25[3]. Здесь не имеет значения то обстоятельство, заимствовали ли они свою

183

точку зрения у Канта или же она была только частью общей культурной атмосферы, которую в явном виде выразил Кант. Всякий допускал, что существуют ясные, простые и основные истины геометрии, не вызывающие никакого сомнения. Из этих простых истин, аксиом гео­метрии можно было шаг за шагом перейти к некоторым выводным истинам, теоремам.

Как мы уже указывали, некоторые математики ве­рили, что они смогли вывести аксиому о параллельных из других аксиом Евклида. Почему так трудно было обнаружить ошибки в их доказательствах? Ответ на этот вопрос связан с тем фактом, что в то время не су­ществовало достаточно сильной логики, которая давала бы строгие правила для геометрических доказательств. В некоторых местах вывода иногда незаметно допуска­лось обращение к интуиции, иногда это делалось совер­шенно явно, иногда скрытым путем. Метод для различе­ния чисто логического вывода и вывода, вносящего не­логические компоненты, основанные на интуиции, стал известен только после систематической разработки ло­гики во второй половине прошлого столетия. Тот факт, что эта новая логика была сформулирована символиче­ски, увеличивает ее эффективность, но эта черта не яв­ляется абсолютно существенной. Существенным для но­вой логики было, во-первых, то, что правила умозаклю­чений в ней могли быть установлены с полной точностью. Во-вторых, на протяжении всего вывода никакое утвер­ждение не принималось, если оно не было получено из посылок или же из ранее полученных результатов путем применения к ним правил логических умозаключений.

До разработки современной логики никакая система существовавшей логики с совокупностью ее правил не была адекватна геометрии. Традиционная логика имела дело только с одноместными предикатами, но в геометрии мы изучаем отношения между многими элементами. Точка, лежащая на прямой, или прямая, лежащая на плоскости, представляют примеры двуместных отношений. Точка, лежащая между двумя другими точками, дает пример трехместного отношения. Мы можем рассматривать равенство двух отрезков как двуместное отношение, но, поскольку отрезки не берутся в качестве исходных объектов, отрезок лучше представить как пару точек. В таком случае равенство между двумя отрезками

184

 

представляет отношение между двумя соответствующими парами точек. Иными словами, оно является четырех­местным отношением между точками. Как вы видите, геометрия нуждается в логике отношений. Эта логика не существовала в то время, которое мы рассматриваем. Когда она была создана, логические ошибки в различных предполагаемых доказательствах аксиомы о параллель­ных были обнаружены. В каком-то пункте каждого та­кого рассуждения допускалось обращение к посылкам, которые основываются на интуиции и не могут быть вы­ведены из других аксиом Евклида. Это могло бы быть интересным, если бы не тот факт, что скрытые, интуи­тивные посылки оказывались замаскированной формой самой аксиомы о параллельных.

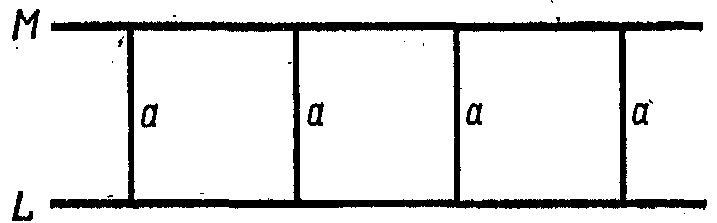
Рис. 13-1.

В качестве примера такой скрытой аксиомы, эквива­лентной аксиоме о параллельных, может служить следующая: если на плоскости существует прямая линия L и криваяM, а все точкиMнаходятся на том же самом расстоянии отL,тогдаMтакже представляет прямую линию. Это показано на рис. 13-1, гдеaпредставляет постоянное расстояние отLвсех точекM.

Эта аксиома, которая интуитивно кажется истинной, принималась иногда в качестве молчаливого предполо­жения при доказательстве аксиомы о параллельных. Когда она предполагается, тогда аксиома о параллель­ных действительно может быть доказана. К несчастью, само это предположение не может быть доказано, если мы не будем исходить из истинности аксиомы о параллельных или некоторой другой аксиомы, эквивалентной ей.

Другая аксиома, эквивалентная аксиоме о параллельных, хотя, возможно, и не так интуитивно очевидна, как только что приведенная, есть предположение о том, что

185

 

геометрические фигуры различных размеров могут быть подобными. Например, два треугольника будут подобными, если они имеют равные углы и пропорциональные стороны. На рис. 13-2 отношение a: bравно отношениюa': b'и отношениеb : cравно отношениюb': c'.Предположим, что я начерчу сначала меньший треугольник со сторонамиa, b, c.Существует ли больший треугольник

Рис. 13-2.

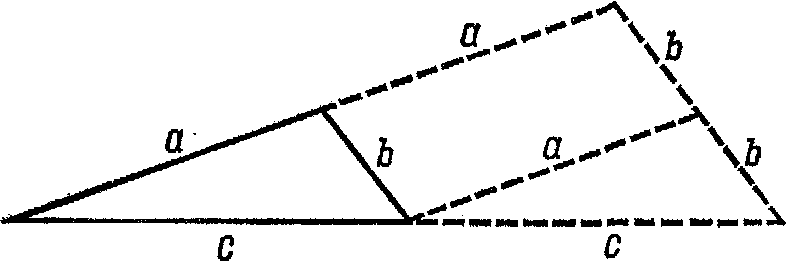
с теми же самыми углами и со сторонами a, b,c? Ка­жется очевидным, что ответ является положительным. Предположим, что мы хотим построить треугольник, стороны которого будут в точности вдвое больше сторон взятого треугольника. Мы можем это легко сделать, как показано на рис. 13-3.

Рис. 13-3.

Мы просто продолжим стороны a и cна ту же самую длину, затем соединим, их конечные точки. После некоторого размышления кажется совершенно ясным, что третья сторона должна иметь длину 2bи больший треугольник будет подобен меньшему. Если мы будем исходить из этой аксиомы о подобных треугольниках, то мы можем доказать аксиому о параллельных. Но снова мы в скрытой форме предполагаем аксиому о параллельных. Действительно, мы не можем доказать подобие двух треугольников без применения аксиомы о параллельных или другой аксиомы, ей эквивалентной. Таким образом, использование аксиомы о подобных треугольниках равносильно

186

 

использованию аксиомы о параллельных, аксиомы, которую мы пытались доказать.

Но вплоть до девятнадцатого столетия строго логически не было доказано, что аксиома о параллельных независима от других аксиом Евклида. Она не может быть выведена из них. Отрицательные утверждения такого рода, устанавливающие невозможность осуществления чего-либо, обычно значительно труднее доказать, чем утверждения позитивные. То, что позитивное утверждение того или иного рода можетбыть выведено из некоторых посылок, доказывается просто путем показа логических шагов вывода. Но как можно доказать, что нечтоневыводимо?Если вам после ста попыток не удалось вывести теорему, вы можете отказаться от дальнейших попыток, но это не служит доказательством невозможности. Может быть, кто-то каким-либо неожиданным окольным путем найдет вывод. Тем не менее, несмотря на эту трудность, формальное доказательство незави­симости аксиомы о параллельных было наконец полу­чено.

Разработка следствий из этого доказательства пред­ставляет одно из наиболее волнующих открытий в мате­матике девятнадцатого столетия. Если аксиома о парал­лельных независима от других аксиом Евклида, тогда без всякого противоречия с другими аксиомами она может быть заменена утверждением, с нею несовместимым. Путем испытания различных возможностей были созданы новые аксиоматические системы, названные неевклидовыми геометриями. Что следовало думать об этих странных новых системах, теоремы которых так проти­воречили интуиции? Должны ли они рассматриваться в качестве не более чем безобидной логической игры – игры, имеющей целью показать, как могут комбинироваться без противоречий различные утверждения? Или же они должны рассматриваться как возможно «истинные» в том смысле, что они могут быть применены к структуре самого пространства?

Последний случай казался настолько абсурдным в то время, что никто не помышлял об обсуждении этого вопроса. Фактически, когда несколько смелых математиков начали исследовать неевклидовы системы, они колебались, публиковать ли им свои результаты. Сейчас можно смеяться над этим и спрашивать, почему публикация

187

 

какой-либо системы математики должна вызывать какие-то чувства. В настоящее время мы часто придерживаемся чисто формалистического взгляда на аксиоматическую систему. Мы не спрашиваем, какие интерпретации или применения она может иметь, но ограничиваемся только вопросом, является ли система аксиом логически непротиворечивой и возможно ли вывести некоторое утверждение из них. Однако позиция большинства математиков девятнадцатого столетия была не такова. Для них «точка» в геометрической системе означала место в реальном Пространстве, а «прямая линия» – прямую в обычном смысле слова. Геометрия не рассматривалась как упражнение в логике; она ставила своей задачей исследование окружающего нас пространства, а не пространства в абстрактном смысле, которое математики имеют в виду сегодня, когда говорят о топологическом, метрическом, пятимерном пространствах и т. п.

Карл Фридрих Гаусс, один из величайших математиков, возможно самый великий математик девятнадцатого столетия, впервые, насколько известно, открыл непротиворечивую систему геометрии, в которой аксиома параллельных была заменена противоположным утверждением. Мы знаем это не из какой-либо его публикации, а только из письма, которое он написал другу. В этом письме он говорит об исследовании такой системы и выводе некоторых интересных теорем из нее. Он добавлял, что не заботится об опубликовании своих результатов, потому что «боится крика беотийцев». Читатель, возможно, знает, что в Древней Греции беотийцы – жители провинции Беотия – невысоко ценились афинянами. Мы можем перевести это выражение на современный язык так: «Эти невежды будут смеяться и скажут, что я сошел с ума». Под невеждами Гаусс подразумевает не необразованных людей, а некоторых профессоров математики и философии. Он знал, что они сочтут его сумасшедшим, если он всерьез будет говорить о неевклидовой геометрии.

Если мы откажемся от аксиомы о параллельных, то чем мы можем заменить ее? Ответ на этот вопрос, на один из наиболее важных вопросов в истории современной физики, будет подробно рассматриваться на протя­жении 14 – 17 глав.

188