Добавил:

neus500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Физика

Файл:

Микроэкономика_Гальперин, Игнатьев, Моргунов_Задачник_2007 -160с

.PDF

Скачиваний:

Добавлен:

24.07.2017

Размер:

3.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

Общее равновесие и общественное благосостояние.	131

После перемножения получаем:

10Y1 − Y1X1 = 10X1 – X1Y1 X1 = Y1.

Отсюда: U1 = X10.5X10.5 = X1 U1 = 10 − X2.

Аналогично можно показать, что U2 = X2. В результате получаем уравнение границы возможных полезностей:

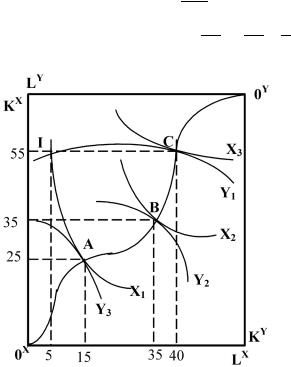
U1 = 10 − U2

Эта граница представлена на рис. 8.1

Рис. 8.1. Граница возможных полезностей

8.2. U10 = 20.5 20.5 = 2; U20 = 80.5 80.5 = 8.

Легко догадаться, что уравнение контрактной кривой

есть X1 = Y1, или, что то же самое, X2 = Y2.

См. рис. 8.2. Диагональ квадрата (коробки Эджуорта) 0102 есть контрактная кривая. Точка А — точка изначального размещения благ.

	1	2		Y1		Y2		PX		*
8.3.	MRSXY	= MRSXY	=		=		=		= p		= 1.
8.3.	MRSXY	= MRSXY	=	X	=	X	=	P	= p		= 1.
				1		2		Y

Следовательно, относительная равновесная цена (p*) есть

любой луч, пересекающий контрактную кривую под прямым углом. На рис. 8.2 эти лучи проведены через точку А и точку желаемого «секретарем рынка» размещения (точку В), где индивид 1 имеет X1 = 6, Y1 = 6; индивид 2, в свою очередь, обладает X2 = 4, Y2 = 4. Исходя из заданных нам функций полезностей индивидов можно заметить, что в точке В U1 = 6, U2 = 4 (что и нужно «секретарю рынка»).

132	Часть VI.

Используя рис. 8.2, нетрудно заметить, что для достижения нового распределения полезностей между индивидами «секретарю рынка» надо передать индивиду 2 от индивида 1 либо 8 единиц Y1, либо 8 единиц X1. Для того чтобы в этом убедиться, достаточно из точки А провести прямые горизонтальную и вертикальную линии до соединения с лучом, представляющим относительную равновесную цену и пересекающему под прямым углом контрактную кривую в точке В. После указанного перераспределения относительная равновесная цена (р*) обеспечит автоматический переход в точку В — к желаемому «секретарем рынка» распределению полезностей.

Рис. 8.2. Коробка Эджуорта и перераспределение

Решение задачи № 9

9.1.См. рис. 9.1.

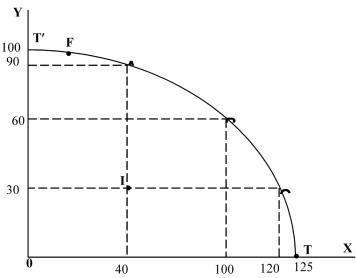
9.2.a) Точка I не является точкой оптимума, так как она не является точкой касания изоквант. Напротив, изокванты

X1 и Y3 пересекаются в точке I. В точках касания изоквант соблюдается условие парето-эффективности для производства

|(MRTSXLK = MRTSYLK ).

б) 22.5 + 25 = 47.5. Отсюда ∆K = 70 − 47.5 = 22.5 50LY отвечает 10LX. Следовательно, ∆L = 55 − 10 = 45.

Общее равновесие и общественное благосостояние.	133

MRTSX	=	∆K	=	22.5	= 0.5.
MRTSX	=	∆L	=	45	= 0.5.
LK		∆L		45
9.3. Соединяем указанные точки кривой (см. рис. 9.1).
9.4. а) См. рис. 9.2.

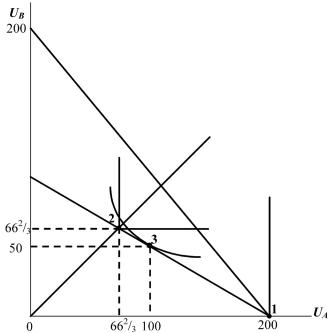
б)См.рис.9.2.КоординатыточкиI(X1 = 40,Y1 = 30).НахождениевточкеIозначаетнеэффективность,посколькуонанаходится слева от кривой продуктовой трансформации (границы производственныхвозможностей).Приимеющихсявданнойэкономике ресурсах можно достичь более высокого объема выпуска.

в) См. рис. 9.2. Нет, не будет. Переход из точки I в точку F сокращает выпуск блага X. Поэтому, несмотря на то что он переводит экономику из неэффективного состояния

вэффективное, парето-улучшения не происходит.

9.5.MRSXY = MRPTXY = ∆∆XY = 100125 = 0.8.

9.6.Нет, не обеспечат: MRPTXY = PX PX = 4. Отсюда PX = 3.2. PY 4 5

Рис. 9.1. Коробка Эджуорта для производства

134	Часть VI.

Рис. 9.2. Кривая продуктовой трансформации

Решение задачи № 10

10.1.

MRTSX

;

MRTSY

;

2KY

;

2(100 − KX )

200K

= 200L − L K

200 − LX

X X

LX(200

− KX) = 200KX.

Отсюда

200KX

200 − K

Определяем значения LX при KX = 0, 25, 50, 75 и 100 По имеющимся в условии задачи данным строим короб-

ку Эджуорта для производства, проводим в ней диагональ и по данным таблицы строим контрактную кривую для производства.

Общее равновесие и общественное благосостояние.	135

10.2. Производство блага X капиталоинтенсивно, так как

KX > KT , где KT и LT — общие количества капитала и труда. В

LX LT

коробке Эджуорта этот факт отражен расположением вогнутой контрактной кривой для производства выше диагонали.

Капиталоинтенсивность производства блага X вдвое выше

капиталоинтенсивности производства блага Y. В этом легко

убедиться, рассчитав соответствующие значения LY и KY (см.

таблицу) и сопоставив

в любых точках (кроме

крайних). Например,

= 2.

120

Решение задачи № 11

11.1. Преобразуем уравнение кривой продуктовой транс-

формации:

9Y2 = 100 − X2;

Y2 =

100 − X2

;

Y = 13 (100 − X2)0.5.

Теперь находим предельную норму продуктовой транс-

формации:

MRPTXY = dXdY = 16(100− X2)−0.5(−2X) = − X3 (100− X2)−0.5. 11.2. Для вогнутой по отношению к началу координат

кривой продуктовой трансформации должны соблюдаться

условия: dY < 0; d2Y > 0. dX dX2

136					Часть VI.

	d2Y	=	1	(100 − X2)−1.5	> 0,
	dX2	=	6	(100 − X2)−1.5	> 0,
	dX2		6

так как по условиям задачи X < 10 во всех точках кривой, кроме точки ее соединения с осью 0Y.

Кривая продуктовой трансформации вогнута, если а) имеет место убывающая отдача от масштаба в производстве обоих благ; б) если нарушается допущение об однородности факторов (например, один из факторов производства имеет убывающую производительность в производстве какого-либо блага); в) при допущении об однородности факторов и постоянной отдаче от масштаба выпуск благ требует использования факторов в различных пропорциях (например, производство одного блага — трудоинтенсивное, другого — капиталоин-

тенсивное, скажем, KX < KY ).

LX LY

11.3.− X3 (100 − X2)−0.5 = − 74;

	X2	(100 − X2)−1 =			16	(100 − X2)−1	=	144
9				49				49X2

100 − X2 =			49X2	193X2 = 14 400			X* = 8.64;
			144

Y* = 13 (100 − X2)0.5 = 13 (100 − 8.642)0.5 = 1.68.

Решение задачи № 12

12.1 Выражаем LX и LY через X и Y соответственно и получаем уравнение для кривой продуктовой трансформации:

X2 + 4Y2 = 100.

Крайние точки данной кривой: X = 10, Y = 0; X = 0, Y = 5. Затем находим общий дифференциал данного уравнения:

2XdX + 8YdY = 0,

или

− dXdY = MRPTXY = 4XY .

Общее равновесие и общественное благосостояние.	137

12.2 Условия оптимума (парето-эффективности) предпо-

лагают, что MRPTXY = MRSXY.

MRS

MUX

Следовательно,

;

X2 = 4Y2;

X2 + 4Y2 = 2X2 = 10.

В результате получаем:

X* = 50 = 7.07;

12.5

= 3.535.

Общественная полезность:

U= 7.07 3.535 ≈ 5.66.

12.3.Поскольку:

= MRPT ,

MRS

следовательно:

12.5

PY*

Таким образом, предложенные «аукционистом» цены

обеспечат парето-эффективность.

Ценность выпуска составит

P*X*

+ P*Y = 1 7.07 + 2 3.535 = 14.14.

12.4. В таком случае из уравнения X2 + 4Y2 = 100 полу-

чаем, что Y2 = 9 Y = 3. При таких значениях:

U =

8 3 ≈ 4.9;

P*X*

+ P*Y = 1 8 + 2 3 = 14.0.

Легко заметить, что в результате отклонения от паретоэффективной комбинации благ общественная полезность и ценность выпуска снизились.

12.5. От подготовки к войне ресурсов не прибавляется, следовательно, граница производственных возможностей и MRPTXY остаются прежними. С ростом «оборонного сознания» меняется только MRSXY.

MRSXY = MUX = 3Y .

MUY X

138								Часть VI.

Отсюда:
	X	=		3Y		;		12Y2 = X2.
	4Y	=		X		;		12Y2 = X2.
	4Y			X
Следовательно:
		12Y2 + 4Y2 = 100;
	Y*	= 2.5;						X* = 8.66.
Соотношение цен:
			P*				X
				X	=			= 0.866.
					=		4Y	= 0.866.
			P*				4Y
			Y

Оно говорит нам о росте относительной цены пушки

(если раньше 1 пушка стоила 0.5 одной единицы масла, то теперь приблизительно 7/8 той же единицы масла).

Определим занятость до возникновения напряженности между страной Дураков и страной Баранов. Из условий задачи

находим, что L

= X2; L = 0.5Y2. Из полученных в п. 6.2 зна-

чений X*, Y* получаем L

≈ 50, L ≈ 6.25. В условиях подготовки

к войне LW ≈ 75,

≈

6.25. Таким образом, изменение заня-

тости в производстве пушек ∆LX

= 75 − 50 = 25, а изменение

занятости в производстве масла

∆LY = 6.25 − 12.5 = −6.25.

12.6. Теперь MRS

. Отсюда:

;

4Y2 = 3X2.

Следовательно:

X2 + 3X2 = 100;

= 5;

Y* ≈ 4.33;

≈ 0.289.

Очевидно, что цена пушки относительно единицы масла

ниже, чем в предыдущих ситуациях (0.289 < 0.5 < 0.866). В условиях долгосрочного мира занятость распределяется следующим образом: LРX = 25, LРY ≈ 18.75. Таким образом, изменение занятости в производстве пушек ∆LX = 25 − − 75 = −50, а изменение занятости в производстве масла

∆LY = 18.75 − 6.25 = 12.5.

Общее равновесие и общественное благосостояние.	139

Решение задачи № 13

13.1.См. ответ на вопрос 13.6.

13.2.UA = 200, UB = 0.

13.3.Оптимальные значения UA и UB находятся в точке пересечения луча, выходящего под углом 45о из начала

координат (его уравнение UA = UB), с границей возможных полезностей (UA + 2UB = 200). Совместное решение этих двух уравнений дает нам UA = 662/3, UB = 662/3.

13.4.Заметим, что UA + UB достигает максимума в пределах области достижимых полезностей тогда, когда она соединяется с границей возможных полезностей в точке ницшеанского оптимума. Следовательно, UA = 200, UB = 0.

13.5.«Творец политики» находит следующее решение:

L = UА0.5 UB0.5 + λ(200 −UA − 2UB);

∂L

= 0.5

U0.5

− λ = 0 λ = 0.5

U0.5

;

∂U

U0.5

∂L

= 0.5

U0.5

− 2λ = 0 2λ = 0.5

U0.5

;

∂U

U0.5

∂L

= 200 −U

− 2U

= 0 U

= 200 − 2U

∂λ

Отсюда:

U0.5

= 0.5

;

U0.5

= 0.5

(200 −U

)0.5

;

(200 − 2U

)0.5

U0.5

= 200 − 2UB

= 200

2UB

4UB

UB = 50, UA = 100.

13.6. См. ниже рис. 13.1.

Решение задачи № 14

14.1. «Творец политики» находит следующее решение

L = YA0.5 + YB0.5 + λ(100 − YA − YB);

140	Часть VI.

Рис. 13.1. Социальные оптимумы:

() 1 — ницшеанский и утилитаристский оптимумы, () 2 — роулсианский оптимум, () 3 — оптимум Бернулли–Нэша.

∂L	=	0.5	− λ = 0	0.5	= λ;
∂Y	=	Y0.5	− λ = 0	Y0.5	= λ;
∂Y		Y0.5		Y0.5
A		A		A
∂L	=	0.5	− λ = 0	0.5	= λ.
∂Y	=	Y0.5	− λ = 0	Y0.5	= λ.
∂Y		Y0.5		Y0.5
B		B		B

Отсюда YA = YB = 50.

14.2. Теперь «творец политики» находит следующее решение

L = Y0.5

+ Y0.5 + λ(100 − 2Y − Y );

∂L

0.5

− 2λ = 0

0.5

= 2λ

= 4λ2

;

∂Y

Y0.5

∂L

0.5

− λ = 0

0.5

= λ

= λ2.

∂Y

Y0.5

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

Соседние файлы в предмете Физика

#
24.07.201711.22 Кб2referer.htm
#
24.07.201760.63 Mб87Капралов Е.Г., Кошкарев А.В., Тикунов В.С. и др. - Геоинформатика (Классический университетский учебник) - М., ИЦ Академия - 2005.pdf
#
24.07.20171.39 Mб14Краткая история времени. От большого взрыва до черных дыр.doc
#
24.07.20173.04 Mб39Микроэкономика_Гальперин, Игнатьев, Моргунов_Задачник_2007 -160с.PDF
#
24.07.20176.74 Mб75Перельман Я. И. - Занимательная физика. Книга 1 - 1983.pdf
#
24.07.2017218.62 Кб33Природа_силы_инерции.doc
#
24.07.20172.3 Mб89Эйнштейн А. - Теория относительности (R&C Dynamics) - 2000.pdf