Верба В.С. - Авиационные комплексы радиолокационного дозора и наведения (Системы мониторинга) - 2008

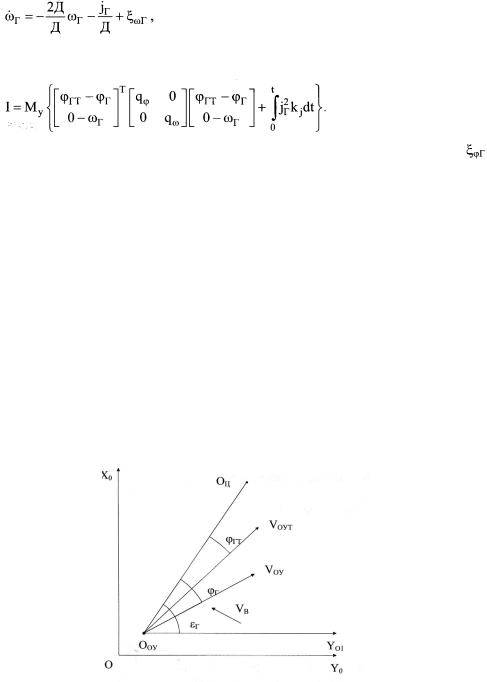
(8.8)

необходимо найти требуемый сигнал управления jVr, оптимальный по миниму­ му функционала качества

(8.9)

В (8.7)-(8.9) (рг и φΓΤ - бортовой пеленг цели и его требуемое значение; и 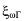- центрированные гауссовские возмущения, характеризующие флуктуа­

ции бортового пеленга и угловой скорости ωΓ линии визирования; Д и Д - дальность до цели и скорость сближения с ней; q9 и qa - штрафы за точность управления; kj - штраф за величину сигнала управления j r , под которым пони­ мается боковое ускорение ОУ.

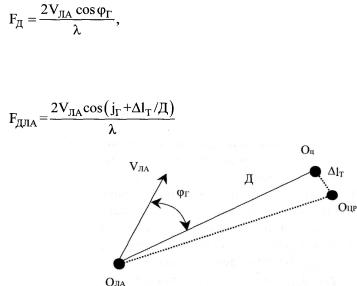
Следует отметить, что соотношение (8.8) является разновидностью клас­ сического кинематического уравнения [34] для случая, когда боковое ускоре­ ние цели равно нулю. Такая ситуация справедлива как для неподвижной цели, так и для малоподвижной цели, движущейся с постоянной скоростью. Смысл введенных обозначений поясняет рис. 8.7, где для горизонтальной плоскости в невращающейся земной системе координат показаны точки расположения цели Оц и объекта управления Ооу; векторы требуемой Уоут и фактической Voy ско­ ростей ЛА. Необходимо отметить, что при наличии ветра, направление и ско­ рость которого характеризуются вектором VB, полет к цели по прямой 0оу Оц возможен в том случае, если требуемый бортовой пеленг фгт будет равен углу сноса φγ. Вполне очевидно, что при полете ОУ к цели по линии ОоуОц (под

Рис. 8.7

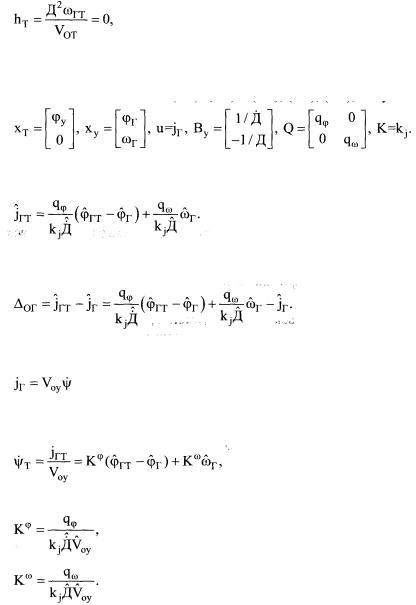
углом φΓΤ = cpy ) угловая скорость линии визирования будет равна нулю, т. е. ωΓΤ = 0. В такой ситуации текущий промах [29]

•

(8.10)

где VOT - модуль относительной скорости. Данное обстоятельство поясняет способность функционала (8.9) учитывать требования точности наведения.

Поставив в соответствие (8.7)-(8.9) и (8.1), (8.2), (8.5), получим

(8.11)

Подставив (8.11) в (8.4), найдем закон изменения требуемого бокового ус­ корения ОУ:

(8.12)

Тогда алгоритм траекторного управления ЛА при наведении на наземную цель описывается соотношением

(8.13)

Метод командного наведения совместно с законом (8.12) может быть получен с учетом связи

(8.14)

между поперечным ускорением j r , курсом ψ и собственной скоростью ОУ. Подставляя (8.14) в (8.12), получим

(8.15)

где

(8.16)

(8.17)

Принимая во внимание, что требуемые значения курса ψτ передаются на

ОУ достаточно редко с периодом Τ , преобразуем (8.15) в разностное уравне­ ние для дискретного времени:

Отсюда следует, что требуемый курс ψ τ , передаваемый на борт управ­ ляемого ЛА при командном наведении, определяется соотношением

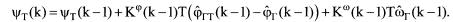(8.18)

Анализ (8.12), (8.18) позволяет сделать следующие заключения. Полученные методы наведения являются частным случаем метода после­

довательных упреждений (8.6) и отличаются от него нестационарным характе­ ром коэффициентов, учитывающих в требуемом законе наведения веса ошибок управления 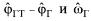. При этом на больших расстояниях до цели, когда Д

велика и закон (8.18) вырождается в разновидность прямого метода, называемую иногда путевым методом. Причем, чем меньше скорость Д, тем сильнее действие ветра и влияние ошибки 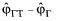на сигнал управления. При

неизменной скорости полета значение весового коэффициента (8.16), учи­ тывающего влияние ошибки по углу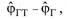 остается неизменным. В то же время по мере уменьшения дальности Д возрастает влияние второго компо­ нента Κω (8.17) сигнала управления. Это возрастание, обусловленное не толь­ ко увеличением ωΓ с уменьшением дальности, но и увеличением весового

до цели. Следовательно, в процессе полета по мере приближения к цели в зако­ не управления происходит перераспределение влияния ошибок управления от Фгт ~~ Фг на начальных участках в пользу ошибки по ωΓ на конечных участках траектории, обеспечивающей минимизацию промаха (8.10).

Синтезированный алгоритм наведения, реализуя минимум функционала качества (8.9), позволяет получить систему наведения, совместно наилучшую как по точности управления, так и по экономичности.

Сигнал управления зависит не от абсолютных значений коэффициентов штрафов ςφ , ςω и kj, а от их отношений 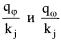, что существенно облегчает

возможных значениях ошибок управления 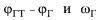для минимальных значений 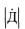и Д требуемые поперечные перегрузки не превышали допусти­ мые значения.

В состав ИУС АК РЛДН, реализующей алгоритм управления (8.18), долж­ ны входить устройства формирования оценок дальности Д от ОУ до цели, ско­ рости Д его сближения с ней, требуемого угла упреждения φΓΤ, бортового пе­ ленга φΓ, угловой скорости ωΓ JIB с ОУ и скорости Voy .ОУ. При этом оценки

фгт могут принимать различные значения, определяемые режимами работы

бортовых РЛС и типом используемого оружия.

Необходимо отметить хорошее согласование метода командного наведе­ ния (8.18) с методом самонаведения (8.12), используемым на ОУ, что дает воз­ можность реализовать смешанное управление. Его суть состоит в том, что в промежутках между поступлениями команд управления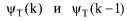

бортовая РЛС ОУ включается на очень короткое время, достаточное для полу­ чения 2-3 тактов высокоточных измерений (десятые доли секунды), дающих возможность при использовании (8.12) скорректировать погрешности наведе­ ния, определяемые ошибками формирования требуемого курса ψ τ .

В заключение следует подчеркнуть, что расчет требуемого курса по

борту управляемого ЛА формирование текущего требуемого курса по правилу

(8.19)

в котором Такой прием обеспечивает более высокую точность наведения ЛА, чем

при использовании только дискретных значений ψτ (k), особенно при выклю­ ченной БРЛС наводимого объекта.

8.3.2.Оптимизация алгоритмов наведения на малоразмерные наземные цели при использовании активного синтезирования апертуры антенны

Одним из способов улучшения разрешающей способности РЛС ЛА, приме­ няемых при наведении на малоразмерные наземные цели (МНЦ), является ис­ пользование синтезирования апертуры (СА) антенны или доплеровского обужения луча [27]. Однако желаемый эффект улучшения линейного разрешения по азимуту при использовании СА или ДОЛ достигается лишь в том случае, если ЛА движется под достаточно большим углом к линии визирования МНЦ, в то время как для ее поражения линия пути ЛА должна совпадать с ЛВ. В связи с этим алгоритмы траекторного управления должны одновременно удовлетворять противоречивым требованиям к заданному линейному разрешению и линейному промаху. Такие алгоритмы должны обеспечивать полет ЛА по криволинейной

траектории, при которой на начальном участке при полете под некоторым углом к ЛВ реализуется требуемое линейное разрешение по азимуту, а на конечном - доворот, позволяющий получить высокоточное наведение на МНЦ.

Необходимо отметить, что при полете по криволинейной траектории возрас­ тает расход энергии, затрачиваемой на управление ЛА, в связи с чем актуальной становится задача улучшения экономичности закона наведения. Удовлетворить противоречащим друг другу требованиям обеспечения высокой разрешающей способности, точности и экономичности наведения в условиях реальных ограни­ чений на располагаемые поперечные перегрузки при использовании традицион­ ных методов наведения [29] невозможно. Следует подчеркнуть, что поочередное эмпирическое использование на различных участках траектории различных мето­ дов наведения не позволяет получить приемлемых результатов из-за трудности определения момента перехода с одного закона на другой, возникновения значи­ тельных переходных процессов и сложности обеспечения экономичности.

Весьма перспективным направлением синтеза сложных законов наведения, наилучших по противоречивым требованиям точности, разрешающей способно­ сти и экономичности, является использование математического аппарата СТОУ.

Ниже будут использованы простейшие алгоритмы этой теории, рассмот­ ренные в п.8.1. Необходимо подчеркнуть, что в приложении к АК РЛДН проце­ дуры синтезирования могут использоваться в двух вариантах. Первый из них ос­ нован на использовании алгоритмов траекторного управления, обеспечивающих стабильное высокое разрешение на самом АК РЛДН. Целесообразность специ­ ального управления обусловлена тем, что при обычном переднебоковом обзоре интересующего участка местности с полетом по прямой линии изменяется ли­ нейное разрешение по азимуту, что приводит к ухудшению детальности радио­ локационного изображении. Второй вариант обеспечивает вывод наводимого ЛА на траекторию, при которой на нем после включения БРЛС обеспечивается син­ тезирование со стабильным линейным разрешением по азимуту.

В связи с этим на первом этапе будет приведен алгоритм траекторного управления самолетом-носителем АК РЛДН, обеспечивающий на нем синтези­ рование апертуры с постоянным линейным разрешением, а на втором этапе - ал­ горитмы траекторного управления, обеспечивающие вывод наводимого ЛА на траекторию, при полете по которой на нем после включения БРЛС будет реали­ зован режим синтезирования с постоянным линейным разрешением по азимуту.

Синтез выполняется при условии, что соблюдаются следующие допущения: 1) известны значения требуемой линейной разрешающей способности по

азимуту, длины волны и полосы пропускания доплеровского фильтра; 2) наземная цель движется в произвольном направлении с постоянной

скоростью, величина которой существенно меньше скорости полета самолета; 3) известны диапазон располагаемых перегрузок ЛА, максимально до­

пустимая угловая скорость ωΛ0Π линии визирования и минимально допустимый при синтезировании бортовой пеленг 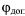цели;

Следует подчеркнуть, что в зависимости от точности аппроксимации мо­ гут быть получены различные формулы, связывающие между собой требуемое разрешение Δίχ с условиями применения ЛА, определяемые конкретными зна­ чениями УДА, фг, Д. Ниже будет рассмотрен наиболее простой случай, который базируется на аппроксимации (8.21) рядом Тейлора в линейном приближении. При таких условиях

где было учтено равенство (8.20).

Для того чтобы разрешить точки Оц и Оцр, полоса пропускания доплеровского фильтра в приемнике БРЛС ЛА не должна превышать величины

(8.22)

или

(8.23)

где

(8.24)

- угловая скорость ЛВ цели.

Из (8.22), (8.23) можно получить

(8.25)

(8.26)

Отсюда следует, что для реализации требуемого разрешения Δ/τ траекто­ рия движения ЛА должна быть такой, чтобы бортовой пеленг цели удовлетво­ рял условию

(8.27)

Анализ (8.27) позволяет прийти к следующим заключениям.

Бортовой пеленг φΓΤ, необходимый для реализации требуемого линейного разрешения Δ1τ по азимуту, зависит как от параметров системы обработки сиг­ налов AF, λ, так и от условий применения Д и УЛд·

При прочих равных условиях для обеспечения более высокого линейного разрешения по азимуту необходимо более сильное искривление траектории

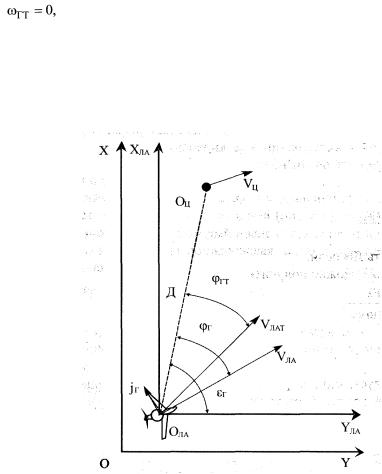
полета ЛА, характеризуемое большими значениями срг. При этом наилучшее разрешение будет обеспечиваться при боковом обзоре (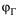=90°), когда цель

находится на траверсе.

В общем случае рассматриваемая система наведения предназначена для стабилизации линейного разрешения по азимуту, обеспечиваемого выбором бортового пеленга (8.27), высокоточного вывода ЛА на цель, обеспечивающего минимизацию промаха (8.10) при условии

(8.28)

иминимизации расхода энергии управляющих сигналов.

Всвязи с этим в состав модели состояния должны, как минимум, входить φΓ

иωΓ. Геометрические соотношения между координатами абсолютного и относи­ тельного движения наземной цели и ЛА в горизонтальной плоскости приведе­ ны на рис. 8.9.

Рис. 8.9

На этом рисунке в земной невращающейся системе координат ΧΟΥ пока­ зано текущее расположение ЛА ОДА И цели Оц. Вектор Уц характеризует ско­ рость и направление движения цели, а УЛдт и УЛд - требуемый и фактический векторы скорости ЛА; φΓτ - требуемое значение бортового пеленга, при котором

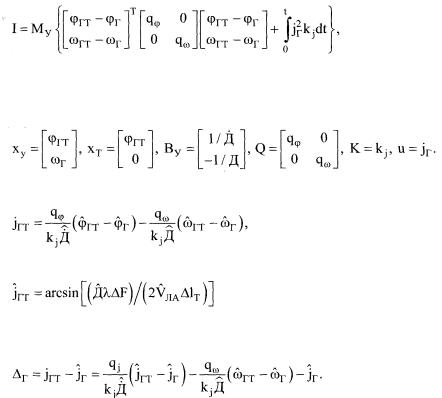
обеспечивается заданное разрешение 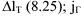- поперечное ускорение ЛА; 8г - угол визирования цели.

Из рисунка видно, что геометрические связи абсолютных и относитель­ ных фазовых координат соответствуют модели (8.7) и (8.8). Необходимо отметить, что и φΓ и а>г достаточно просто оцениваются существующими из­ мерителями.

Функционал качества (8.5), оценивающий эффективность закона наведе­ ния, должен учитывать ошибки сргт—фг управления по бортовому пеленгу, ис­ пользуемые для стабилизации линейного разрешения (8.25) по азимуту; ошиб­ ки ωΓτ—ωΓ управления по угловой скорости визирования, по которым можно оценить величину текущего промаха, и расход энергии сигналов управления j r . С учетом этих особенностей минимизируемый функционал может быть полу­ чен в виде соотношения

(8.29)

в котором ςφ и qro - штрафы за точность управления по углу и угловой скоро­ сти; kj - штраф за значение сигнала управления.

Сопоставив (8.29) с (8.5), а (8.7), (8.8) с (8.1), будем иметь

Используя эти соотношения, получим закон наведения:

(8.30)

где

(8.31)

определяется из (8.25). Тогда алгоритм траекторного управления ЛА при наве­ дении на наземную цель описывается соотношением

(8.32)

Поскольку сам АК РЛДН выполняет только информационную роль и не приспособлен для непосредственного уничтожения наземных объектов, то для него не требуется вывода на цель. В связи с этим для АК РЛДН значения ωπ определяются по правилу

(8.33)

вытекающему из соотношения (8.26). При этом бортовая РЛС АК РЛДН долж­ на формировать оценки дальности до цели и скорости сближения с ней, борто­ вого пеленга цели и угловой скорости линии ее визирования.

Необходимо подчеркнуть, что полет АК РЛДН по криволинейной траек­ тории, определяемой алгоритмом траекторного управления (8.32), (8.33), обес­ печивает стабилизацию линейного разрешения и, соответственно, стабильность радиолокационной карты и более высокую достоверность распознавания на­ земной обстановки.

Изменения относительных фазовых координат системы (8.7), (8.8) при ис­ пользовании закона наведения (8.32) иллюстрируют эпюры, приведенные на рис. 8.10-8.14, а возможный вид траектории в горизонтальной плоскости - на рис. 8.15. На этих рисунках Дп - дальность начала управления;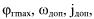 максимальные значения бортового пеленга, угловой скорости ЛВ и поперечно­ го ускорения; Δ/τ - требуемое линейное разрешение по азимуту.

Исследования полученного алгоритма показали, что он позволяет обеспе­ чить стабилизацию требуемого линейного разрешения (рис. 8.14).

При выводе с АК РЛДН самолета на наземную малоразмерную цель с по­ следующим синтезированием на нем апертуры антенны необходимо переда­ вать на него соответствующие команды по курсу ψ τ .

Для реализации (8.34) на борту АК РЛДН необходимо иметь устройства (алгоритмы) оценивания дальности от наводимого ЛА до цели, скорости его сближения с целью, бортового пеленга, угловой скорости линии визирования ЛА-цель и его собственной скорости. Такой состав измерителей не налагает никаких ограничений на практическую реализуемость метода. В остальном свойства этого алгоритма соответствуют рассмотренному в п.8.3.1.

Следует отметить, что при использовании других моделей состояния мо­ гут быть получены другие алгоритмы траекторного управления.