
- •Введение
- •Глава 2. Параллактический треугольник светила и его решение
- •§4. Параллактический треугольник и его решение по основным формулам
- •§5. Вычисление высоты и азимута светила по системам формул
- •§7. Разложение высоты и азимута в ряд Тейлора. Теория таблиц численного типа
- •§1. Небесная сфера
- •§2. Системы сферических координат
- •§3. Графическое решение задач на небесной сфере
- •Глава 3. Видимое суточное движение светил. Изменение координат светил
- •§9. Характеристика суточного движения светил
- •§10. Явления, связанные с суточным движением светил
- •§11. Изменение координат светил вследствие видимого суточного движения
- •Глава 4. Обращение Земли вокруг Солнца. Видимое движение Солнца и изменение его координат
- •§13. Обращение Земли по орбите и видимое годовое движение Солнца
- •§14. Изменение экваториальных координат Солнца в течение года
- •Глава 5. Орбитальное и видимое движение планет, Луны и искусственных спутников
- •§18. Фазы и возраст Луны
- •§21. Орбитальное движение искусственных спутников
- •Глава 6. Измерение времени
- •§22. Основы измерения времени
- •§23. Звездные сутки. Звездное время. Основная формула времени
- •§26. Поясное, декретное, летнее, московское и стандартное времена, их связь с местной системой
- •§28. Понятие о точных шкалах времени
- •Глава 7. Вычисление видимых координат светил. МАЕ
- •§31. Понятие о вычислении видимых координат светил на ЭВМ
- •§32. Устройство таблиц МАЕ для расчета часовых углов и склонений светил
- •§33. Определение времени кульминации светил
- •§34. Обоснование расчета времени видимого восхода (захода) Солнца и Луны и времени сумерек
- •§35. Определение времени восхода и захода Солнца и Луны и времени сумерек по МАЕ
- •Глава 8. Измерители времени. Судовая служба времени
- •Глава 9. Звездное небо. Звездный глобус
- •§42. Устройство звездного глобуса, его установка. Понятие о других пособиях
- •§43. Решение задач с помощью звездного глобуса
- •Глава 10. Секстан
- •§44. Основы теории навигационного секстана
- •§45. Устройство навигационных секстанов
- •§46. Понятие об инструментальных ошибках секстана и их учете
- •§47. Понятие о секстанах с искусственным горизонтом
- •Глава 11. Наблюдения с навигационным секстаном
- •§48. Выверка навигационного секстана на судне
- •§50. Приемы измерения высот светил над видимым горизонтом
- •§53. Наклонение видимого горизонта. Наклонение зрительного луча
- •§55. Общий случай исправления высот светил, измеренных над видимым горизонтом
- •§56. Частные случаи исправления высот светил
- •§57. Приведение высот светил к одному зениту (месту) и одному моменту
- •§58. Определение средних квадратических ошибок поправок и измерения углов
- •§59. Определение средней квадратической ошибки измерения высот светил в море
- •Глава 13. Астрономическое определение поправки компаса
- •§60. Основы астрономического определения поправки компаса
- •§62. Пеленгование светил. Точность поправки компаса
- •§63. Определение поправки компаса. Общий случай
- •Глава 14. Теоретические основы определения места судна по светилам
- •§65. Общие принципы астрономического определения места
- •§67. Метод линий положения. Высотная линия положения
- •§72. Ошибки в высотной линии. Оценка ее точности и вес
- •Глава 16. Методы отыскания места судна и оценки его точности при наличии ошибок в высотных линиях
- •Глава 17. Определение места по одновременным наблюдениям светил. Общий случай
- •§76. Особенности определения места по одновременным наблюдениям светил
- •§77. Общий случай определения места по звездам
- •§78. Определение места днем по одновременным наблюдениям Луны и Солнца
- •§79. Определение места днем по одновременным наблюдениям Венеры и Солнца
- •§80. Определение места по одновременным наблюдениям Венеры, Луны и Солнца
- •Глава 18. Определение места судна по разновременным наблюдениям Солнца
- •§81. Особенности определения места по разновременным наблюдениям Солнца
- •§82. Влияние ошибок счисления и наивыгоднейшие условия для определения места по Солнцу
- •§83. Определение места по Солнцу в общем случае
- •§84. Определение места комбинированием навигационных и астрономических линий положения
- •Глава 19. Ускоренные способы обработки наблюдений
- •§86. Обзор приемов ускорения обработки наблюдений
- •§87. Прием перемещения счислимого места
- •§88. Определение места с предварительной обработкой (предвычислением) линий положения
- •§92. Решение астрономических задач на клавишных ЭВМ
- •Глава 20. Частные методы определения координат места судна
- •§93. Определение широты места по меридиональной и наибольшей высотам Солнца. Понятие о близмеридиональных высотах
- •§96. Определение координат места в малых широтах по соответствующим высотам Солнца
- •§97. Графический способ определения места при высотах Солнца, больших 88°
- •§98. Особенности определения места в высоких широтах
- •Глава 21. Перспективы развития методов астрономических определений в море. Краткий исторический очерк
- •§99. Понятие об астронавигационных системах и навигационных комплексах
- •§100. Краткий очерк истории мореходной астрономии
- •Список литературы

Б.И.КРАСАВЦЕВ
МОРЕХОДНАЯ АСТРОНОМИЯ
Издание второе, переработанное и дополненное
Утверждено Управлением учебных заведений Министерства морского флота в качестве учебника
для судоводительской специальности высших учебных заведений
МОСКВА «ТРАНСПОРТ» 1978
6Т4.2
К78 УДК 528.28.656.61.052(075.8)
Красавцев Б. И.
К78 Мореходная астрономия. Изд. 2-е перераб. и доп. Учебник для судоводительской специальности высш. учеб. заведений ММФ. — М.: Транспорт, 1978. 304 с. ил., табл.
Впер.: 1 р. 30 к.
Всвязи с появлением новой техники, пособий и методов обработки наблюдений издание учебника «Мореходная астрономия» значительно переработано: сокращена первая часть курса — сферическая астрономия; даны новые Морской астрономический ежегодник (МАЕ), Мореходные таблицы (МТ— 75) и секстан CIIO-T; практическая часть курса пересмотрена в сторону упрощения способов и схем обработки наблюдений; рассмотрены приемы получения наиболее точного места, в частности с дополнительными наблюдениями Солнца «через зенит», дневные наблюдения Венеры, Луны и Солнца, значительно переработаны вопросы теории ошибок и уравнивания наблюдений.
Учебник предназначен для учащихся высших морских учебных заведений.
К 31806 − 221 221 − 78 049(01) − 78
6Т4.2
© Издательство «Транспорт», 1978
2
ВВЕДЕНИЕ
Все науки, служащие целям судовождения, имеют общую основную задачу — обеспечение безопасного, быстрого и наиболее экономичного перехода судна морем из одного пункта в другой. Для выполнения этой задачи необходим непрерывный контроль за счислением пути судна, поправками, временем и др.
Навигация рассматривает способы контроля счисления по наблюдениям земных объектов (береговых пунктов, маяков, систем), мореходная астрономия
— обеспечение контроля счисления при плавании судна в открытом море по наблюдениям небесных светил. Так как небесные светила находятся в непрерывном движении, то чтобы определить их место в данный момент, необходимо знать законы их движения, изучаемые в астрономии, а так как результаты наблюдений светил применяются для целей навигации, то в этой части мореходная астрономия примыкает к ней, так что ее часто называют астронавигацией. В спутниковой навигации это наиболее наглядно, так как движение спутников изучается в астрономии, а определение по ним производится радионавигационными методами. Мореходная астрономия, кроме того, дает сведения о службе времени, освещенности горизонта и различных явлениях, происходящих на Земле и во Вселенной. В этой части она является общеобразовательной наукой, воспитывающей правильное материалистическое понимание Вселенной и ее закономерностей.
Следовательно, предметом мореходной астрономии является приложение астрономических знаний к нуждам судовождения.
Астрономия — наука о строении и развитии Вселенной. Она подразделяется на ряд специализированных разделов, имеющих свои задачи и методы, по существу отдельных наук: астрометрия, небесная механика и теоретическая астрономия, астрофизика, космогония, общая астрономия. Из этих наук в мореходной астрономии изучаются или используются астрометрия,
3
теоретическая астрономия и общая астрономия.
Астрометрия подразделяется на сферическую, обсерваторную и практическую астрономию. Сферическая астрономия рассматривает координатные системы на поверхности вспомогательной сферы, их связь и изменения во времени, а также принципы измерения времени. Практическая астрономия изучает методы и инструменты для определения географических координат места, истинных направлений (азимутов) и точного времени. Она подразделяется на:
—геодезическую, или полевую, астрономию, в которой эти задачи решаются при помощи переносных инструментов с довольно высокой точностью, а обрабатываются в камеральных условиях с помощью ЭВМ;
—мореходную астрономию, в которой эти задачи решаются ручными инструментами одним человеком, быстро, но с меньшей точностью, или с помощью астросистем — почти автоматически;
—авиационную астрономию, в которой те же задачи решаются с еще меньшей точностью, но очень быстро, главным образом с помощью автоматических астросистем.
Таким образом, мореходная астрономия является частью практической астрономии. В мореходной астрономии используется также теоретическая астрономия, которая изучает методы определения орбит небесных тел по их видимым положениям (вычисление орбит) и наоборот — видимых положений тел по известным элементам их орбит (вычисление эфемерид). Этот последний раздел и изучается в мореходной астрономии.
Основными задачами, решаемыми мореходной астрономией, являются:
—определение места в море по наблюдениям светил;
—определение поправок приборов направления;
—обеспечение службы времени.
Вспомогательными задачами являются: определение освещенности, кульминаций светил, а также вычислительная и общая подготовка штурмана. В мореходной астрономии на базе сферической и практической астрономии
4
разработаны инструменты, методы и пособия, с помощью которых решаются навигационные задачи в открытом море. Астрономические методы, хотя и уступают радиотехническим по простоте и независимости от погоды, имеют ряд преимуществ: полную автономность, возможность применения их в любой точке Земли, как правило, большую точность, простые и дешевые приборы и пособия, а также скрытность определения. По этим причинам астрономические методы определения применяют сейчас наряду с радиотехническими, в том числе со спутниковыми.
Курс «Мореходная астрономия» состоит в основном из следующих разделов:
—основы сферической и общей астрономии, где изучаются координаты светил, их изменение, измерение времени, эфемериды;
—морские астрономические инструменты, где изучаются секстан, хронометр, звездный глобус, наклономер, работа с ними и различные поправки;
—астронавигация, где рассматриваются методы определения поправки компаса, определения места судна и анализ ошибок определения.
Для решения астрономических задач в море применяются следующие основные пособия: Морской астрономический ежегодник (МАЕ), мореходные таблицы (МТ–75), специальные таблицы ВАС–58, ТВ А–57, а также специализированные и общие ЭВМ.
В практических вопросах автор придерживался следующей последовательности изложения: принцип способа, математическое обоснование, погрешности его, практическое выполнение и пример. Поэтому книга может служить и практическим пособием для штурманов.
Автор выражает глубокую признательность проф. Р.А.Скубко, доцентам А.А.Чебан, Г.В.Макарову, В.Т.Кондрашихину и инж. В.П.Брусенцову за ценные замечания при ознакомлении с отдельными частями рукописи, а также доц. Ф.Н.Мурманскому, давшему ряд полезных указаний при ее рецензировании.
Автор
5
Часть I
ОСНОВЫ СФЕРИЧЕСКОЙ И ОБЩЕЙ АСТРОНОМИИ
Глава 1 НЕБЕСНАЯ СФЕРА И СФЕРИЧЕСКИЕ КООРДИНАТЫ СВЕТИЛ
§1. НЕБЕСНАЯ СФЕРА
Наблюдатель М, находящийся на поверхности Земли, участвует в ее суточном вращении и орбитальном обращении, вследствие чего направления на светила С1, С2 (рис. 1,а) изменяются. Для упрощения решения астрономических задач и наглядности движений вводится вспомогательная сфера, получившая название небесной сферы. Можно представить сферу построенной около места наблюдателя М (см. рис. 1,а) или описанной около центра О Земли (рис. 1,б).
Небесной сферой называется вспомогательная сфера произвольного радиуса, к центру которой параллельно перенесены основные линии наблюдателя и Земли и направления на светила.
Основным направлением наблюдателя М является его вертикаль, или отвесная линия, zО1 (см. рис. 1), положение которой в данной точке Земли постоянно и определяется направлением силы притяжения. Пересечение вертикали с поверхностью Земли представляет место М наблюдателя.
Положение точки М на Земле определяется ее географической широтой ϕ
(угол между отвесной линией и плоскостью экватора) и долготой λ (двугранный угол между меридианами — гринвичским ГР и наблюдателя М, равный дуге e0е). Введение небесной сферы позволяет построить аналогичные системы координат для светил.
При построении небесной сферы ее центр выбирают в произвольной точке О (рис. 2) и через нее проводят линии, параллельные линиям наблюдателя М (см. рис. 1,б). Линия, параллельная вертикали zO1, называется отвесной линией zn, а точки пересечения ее со сферой — зенитом z и надиром n. Линия, параллельная оси pnps Земли (см рис. 1,а), представляет на сфере ось
6
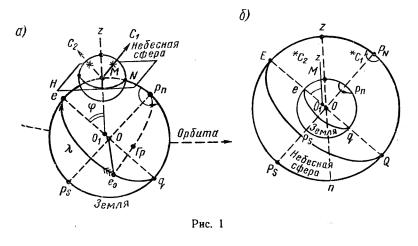
мира РNРS, вокруг которой вращается сфера. Точки пересечения ее со сферой называются полюсами мира: северным PN и южным PS (они соответствуют полюсам Земли).
Плоскость Н истинного горизонта наблюдателя М (см.рис.1,а), проведенная через центр сферы, дает в сечении со сферой истинный горизонт
— большой круг NOstSW, перпендикулярный отвесной линии zn.
Плоскость экватора Земли, перенесенная к центру О сферы дает в сечении со сферой небесный экватор — большой круг EWQOst, плоскость которого перпендикулярна оси мира.
Плоскость рnМерs (см.рис.1,а) — географического меридиана наблюдателя М, проведенная через центр сферы, дает в сечении с ней меридиан наблюдателя — большой круг PNzPSQ. Ось мира PNPS разделяет меридиан наблюдателя на полуденную часть PNzPS, включающую зенит, и полуночную РNnРS, (на рис. 2 волнистая линия). Эти части меридиана Солнце пересекает в полдень и в полночь, отсюда их названия.
Основные круги сферы делят ее на части: горизонт – на надгоризонтную иподгоризонтную, гдесветиланевидны: небесныйэкватор— насеверную(PN) и южную (PS); меридиан наблюдателя NZS — на восточную (Оst) и западную (W).
Истинный горизонт наблюдателя делится на направления (румбы). Пересечение плоскостей меридиана и горизонта дает полуденную линию N—S, а плоскостей экватора и горизонта — линию Ost — W. На сфере пересечение этих
7
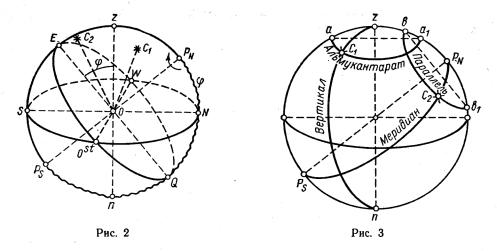
линий дает точки N, ОST, S, W, которыми горизонт разделяется на четыре четверти: NO, SO, SW, N W. Кроме того, горизонт делится на градусы (можно представить его в виде картушки компаса).
Полюс мира, расположенный над горизонтом, называется повышенным полюсом. Его наименование совпадает с широтой наблюдателя: в северной широте — РN, в южной — PS. Возвышение полюса над горизонтом, т.е. дуга NPN, равно широте, так же как дуга zЕ (см. рис. 2).
Если из центра сферы провести направления на светила, то на ее поверхности получаются точки С1, С2, называемые видимыми местами светил (в дальнейшем просто светила). На сферу можно также спроектировать и другие плоскости и объекты: плоскость орбиты Земли даст эклиптику, орбиты Луны— видимуюорбитуЛуны, орбитыспутника— видимуюорбитуспутникаит.п.
Примечание. Изображения одной и той же небесной сферы могут быть разными: для местного наблюдателя и на плоскости его меридиана с центром в глазе наблюдателя (см. рис. 1, 2) или для любого наблюдателя на Земле с центром в центре Земли (см. рис. 9) или в центре солнечной системы (см. рис. 23). Надо твердо усвоить, что все это — изображения одной вспомогательной сферы в различных видах и что из одного вида легко получить другой (сравнить рис.1, 6 и 9). Для каждого типа задач удобно определенное изображение сферы, без лишних деталей.
Введение небесной сферы приводит к упрощениям: замене направлений
— точками, плоскостей и углов — кругами. Движения светил можно рассматривать теперь как движение их мест вместе со сферой — от суточного
8
вращения Земли и по сфере — от собственных движений и других причин.
Системы вспомогательных кругов. Для удобства построения сферических координат на сфере вводятся системы взаимно перпендикулярных кругов. Круги, связанные с отвесной линией: вертикалы — большие круги, плоскости которых проходят через отвесную линию (перпендикулярные горизонту), например zС1n на рис. 3; альмукантараты — малые круги aal, плоскости которых параллельны горизонту. Вертикал, проходящий через точки
Ost, W называется первым вертикалом.
Круги, связанные с осью мира: небесные меридианы (или круги склонений) — большие круги, плоскости которых проходят через ось мира (перпендикулярные экватору), например РNС2РS на рис. 3; параллели — малые круги bbl плоскости которых параллельны экватору. Эти круги аналогичны географическим меридианам и параллелям на Земле.
Небесный меридиан РNzРS лежит в плоскости географического меридиана наблюдателя М (см. рис. 1,б) и поэтому называется меридианом наблюдателя (иногда местным меридианом); одновременно он является и вертикалом наблюдателя.
§2. СИСТЕМЫ СФЕРИЧЕСКИХ КООРДИНАТ
Системы координат на небесной сфере строятся относительно двух взаимно перпендикулярных кругов сферы, подобно широтам и долготам на земном глобусе. В этом случае получаются сферические прямоугольные координаты. Применяются и сферические полярные координаты — по сферическому углу при какой-либо точке и расстоянию от нее. На сфере эти системы часто совпадают. Из известных в сферической астрономии пяти систем небесных координат в мореходной астрономии применяются: горизонтная, две экваториальные и, изредка, эклиптическая.
Горизонтная система координат. Основными кругами (осями координат) в этой системе являются истинный горизонт и меридиан
9
наблюдателя; основным направлением — отвесная линия zn. Положение точки или светила на сфере определяется двумя координатами: высотой и азимутом
(рис. 4; сфера на нем для ϕN повернута W-м к зрителю).
Высотой h светила называется дуга его вертикала от истинного горизонта до места светила. Угол при центре сферы, измеряющий эту дугу, также называют высотой. Этот угол измеряется при наблюдениях. Высоты считаются в пределах от 0 до ±90° с «+» над горизонтом, с «—» под горизонтом, например светило C1 имеет h=46°, светило С1' —h=–30°; высота зенита +90°, надира –90° и т.п.
Азимутом А светила называется дуга истинного горизонта между меридианом наблюдателя и вертикалом светила. Эта дуга измеряет плоский угол при центре сферы или сферический угол А при зените, которые поэтому также называют азимутами.
В мореходной астрономии применяют три системы счета азимутов: полукруговой, круговой и четвертной.
Полукруговой азимут считается в пределах 0–180° от полуночной части меридиана наблюдателя или от вертикала повышенного полюса в сторону Ost-a или W-a до вертикала светила, например А=N100°W (см. рис. 4). В северной широте начальной точкой счета является N, в южной — S, поэтому первая буква наименования азимута совпадает с широтой, вторая — с половиной сферы, где расположено светило. Этот счет азимутов применяется при решении сферических треугольников по формулам и по таблицам ВАС–58.
Круговой азимут считается от точки N в сторону Ost–a до вертикала светила в пределах 0–360°, т.е. совпадает с истинным пеленгом светила, например для светила С1 А=ИП=2600. Этот счет применяется при определениях
∆K и при прокладке.
Четвертной азимут считается по четвертям — от ближайшей части меридиана наблюдателя до вертикала светила в пределах 0–90°, например светило С1 имеет А=80°SW. Этот счет применяется в формуле синусов и ТВА– 57. Необходимо уметь свободно переходить от одной системы счета азимута к
10
другим — это постоянно требуется на практике. Например, для светила С2 (см. рис. 4) имеем: полукруговой А=N150°Ost; круговой А=150°; четвертной А=30°SO. Положение светила С1 в горизонтной системе запишется так: А=260°; h=46°. Одна горизонтная координата определяет на сфере положение одного круга: азимут — положение вертикала, высота — альмукантарата.
Полярные координаты. Положение точки на сфере может быть определено и без построения горизонта — непосредственно при зените. Зенит является полюсом, а меридиан наблюдателя — полярной осью координат Лиг. Азимут в полярных координатах определяется как угол при зените в полукруговом счете (см. рис. 4).
Зенитным расстоянием z называется дуга вертикала от зенита до места светила в пределах 0—180°. Зенитное расстояние связано с высотой соотношением:
z=90°–h. |
(1) |
Дуга z измеряет центральный угол z между отвесной линией и направлениями на светила (этот угол измеряется береговыми инструментами). Полярные координаты применяются при решении сферических треугольников.
Меридиональная высота. Высота светила, расположенного на меридиане наблюдателя, называется меридиональной высотой Н. Ей придается наименование той точки горизонта, над которой она измерена, например для С3 Н=35°S. Наименование меридионального зенитного расстояния Z обратно Н. Так, для светила С3 Z=55°N.
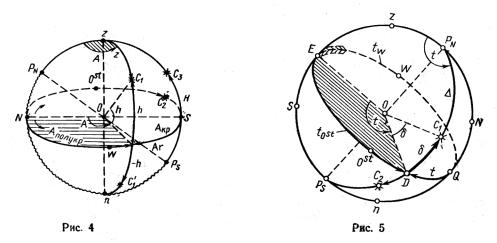
Первая экваториальная система координат. Основным направлением в этой системе является ось мира PNPS, а основными кругами — экватор и меридиан наблюдателя. Положение точки на сфере определяется двумя координатами: склонением и часовым углом (рис. 5).
Склонением δ светила называется дуга меридиана светила от небесного экваторадо места светила. Уголδ при центресферы, равный этой дуге, также называют склонением (его измеряют в обсерваториях). Склонения считаются от 0 до 90° к N или S, например на рис. 5 для светил С1 и С2 имеем δ1=33°N, δ2=26°S.
11
Примечание. В мореходной астрономии принято склонению придавать знак «+», если оно одноименно с широтой, и знак «—», если разноименно. В обсерваторной и геодезической астрономии, а также в электронных цифровых вычислительных машинах (ЭЦВМ) знак «+» придается северному склонению (и широте), знак «—» — южному.
Часовым углом t называется дуга экватора от полуденной части меридиана наблюдателя до меридиана светила, считаемая в сторону точки W от 0 до 360°. В таком счете часовой угол называют вестовым или обыкновенным и наименования обычно не приписывают. Кроме этого, применяется полу круговой счет часовых углов: от 0 до 1800 к W или Ost-y, который называют иногда практическим, так как он применяется при решении треугольников и в таблицах. Из рис. 5 видно, что tОSt=360°tw при tW>180°. Для светила С1 имеем t=245°W или t=115°Оst. Дуга экватора ED измеряет центральный угол t или сферический угол при полюсе t, которые также называют часовыми углами.
Место светила С1 на сфере запишется теперь так: t=245°; δ=33°N. Одна экваториальная координата определяет на сфере положение одного круга: часовой угол — положение меридиана светила; склонение — параллели.
Полярные координаты. Положение точки можно определить при полюсе мира — в полярных координатах t и ∆. Часовой угол t определяется как угол при повышенном полюсе в полукруговом счете (на рис. 5 t=115°Ost).
Полярным расстоянием ∆ называется дуга меридиана светила от повышенного полюса до места светила, считаемая от 0 до 180°, например для
12
светила С1 ∆=57°, С2 ∆=116°. Очевидно, что ∆=90°–δ. По определению часовой угол отсчитывается от плоскости географического меридиана места, поэтому на рис. 5 и аналогичных всегда изображается местный часовой угол. Для других меридианов часовые углы другие.
Вторая экваториальная система координат. В этой системе при той же оси мира основными кругами являются небесный экватор и меридиан точки Овна (E). Точка Овна, или точка весеннего равноденствия, расположена в пересечении экватора с эклиптикой, т.е. связана с орбитой Земли. Положение светила в этой системе определяется склонением и прямым восхождением (рис. 6). Склонение δ в этой системе аналогично первой экваториальной системе.
Прямым восхождением α светила называется дуга экватора от точки Овна до меридиана светила, считаемая в сторону, обратную W-м часовым углам (т.е. в сторону Ost) от 0 до 360°. Дуге α соответствуют при центре сферы и при полюсе углы α, также называемые прямым восхождением. Например, для светила С1 α=95°; δ=35°N. Вместо α в современных морских пособиях применяется звездное дополнение: τ=360°—α.
Звездным дополнением τ называют дугу экватора от точки Овна до меридиана светила, но считаемую в сторону W-x часовых углов, например для светила С1 имеем τ=265°. В отечественных пособиях τ применяется только для звезд, отсюда и его название. Направление счета α — прямого восхождения — совпадает с вращением Земли и ее обращением по орбите, отсюда и название координаты.
Полярные координаты. В этом случае прямое восхождение (или τ) считается как угол при полюсе между меридианами точки Овна и светила, а
полярное расстояние ∆ аналогично первой системе координат (см. рис. 6). Эта система координат аналогична географическим: α — с λ; δ — с ϕ.
Первая и вторая экваториальные системы отличаются только положением начального меридиана: t считается от точки Е, а α — от точки Овна tE,
положениежеточкиОвнаопределяетсяеечасовымугломtEW, поэтому(рис. 6) имеем
13
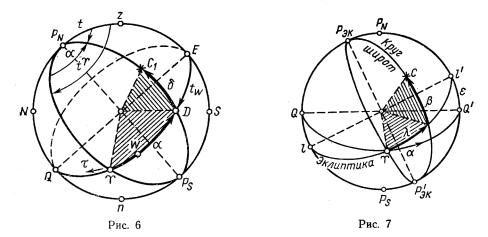
tE=t+α |
(2) |
т.е. часовой угол точки Овна (звездное время) равен сумме часового угла и прямого восхождения светила. По этой формуле (в §23 она названа основной формулой времени) можно перейти от одной системы к другой.
Эклиптическая система координат. В этой системе основным направлением является ось эклиптики ll', а основными кругами — эклиптика (плоскость орбиты Земли) и круг широты точки Овна (рис. 7). Эклиптика, как всякий большой круг, имеет ось РЭКР'ЭК, которая пересекает сферу в полюсах эклиптики — северном РЭК и южном Р'ЭК. Большие круги, проходящие через полюса эклиптики, называются кругами широты (см. рис. 7).
Эклиптической широтой β называется дуга круга широт от эклиптики до места светила в пределах 0 — 90° со знаком «+» к северу, « — » — к югу.
Эклиптической долготой λ называется дуга эклиптики от точки Овна до круга широты светила от 0 до 360 в сторону счета а. Для светила С имеем
β=+40°, λ=60°. Эта система широко применяется при предвычислении координат по формулам §12 и 31, в частности на ЭВМ.
Единицы измерения сферических координат. Координаты на небесной сфере являются дугами больших кругов или сферическими углами, поэтому для их измерения применяют все единицы измерения углов (градусная мера, радианная) и специально астрономическая часовая мера дуг и углов.
Часовая мера основана на исторически сложившемся разделении одного
14
оборота сферы на 24 части (часа), каждого часа — на 60 мин и 1 мин — на 60 с. Между часовой и градусной мерой дуг (в дальнейшем и времени) установлено соотношение: за 24Ч сфера поворачивается на 360°, поэтому 360°=24Ч; 15°=1Ч; 1о=4м; 1'=4c; 0,25'=1c. В мореходной астрономии координаты измеряются до 0,1' или до 0,5c, в практической части — до 1c. Таблицы перехода приведены в МТ– 75 (табл. 39) и МАЕ (приложение 3).
Пример 1. λ=98052,5' Ost перевести в часовую меру. Решение.
|
900 |
Ч |
|
0 |
|
45' m |
c |
Ч |
M |
|
|
|
|
+ 8 |
|
4 + |
|
|
+ (7,5' 4) |
= 6 35 |
30° |
|
|
|
||||||||
λ = |
15 |
|
|
15 |
||||||
|
|
|
|
|
|
|
|
|
||
§3. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ НА НЕБЕСНОЙ СФЕРЕ
При решении конкретных задач применяется более удобная для данного случая система координат. Горизонтная система ориентирована в пространстве относительно отвесной линии наблюдателя, поэтому h и А светила зависят от положения наблюдателя на Земле и по ним можно определить его место. Часовые углы измеряют угол поворота сферы, поэтому их удобно применять при измерении времени, и т.п. В задачах возникает необходимость перехода от одной системы координат к другим. Самым простым является графическое построение сферы, оно необходимо также при изучении систем координат. При построении сферы можно использовать различные ее изображения — пространственные и плоские. Для построения необходимо знать широту наблюдателя (иногда и λ).
Связь широты наблюдателя с координатами точек сферы. В этом вопросе удобнее применить плоское изображение сферы, для чего местная сфера (см. рис. 1,а и рис.2) проектируется на плоскость меридиана наблюдателя (рис. 8). Угол между отвесной линией zn и плоскостью небесного экватора EQ
равен географической широте по ее определению. Дуга EZ поэтому равна ϕ, но эта же дуга — склонение зенита, поэтому δz=ϕ, т.е. склонение зенита равно
15
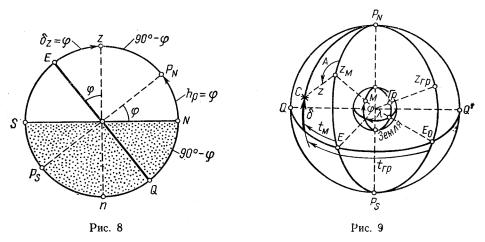
широте места.
Из рис. 8 видно, что широте равны еще три дуги, остальные равны 90°–ϕ.
Дуга NPN, равная широте, вместе с тем — высота точки PN, т.е. hPN–ϕ, или высота повышенного полюса равна широте места. Рис. 8 удобен для нанесения высот и склонений на меридиане наблюдателя, но неудобен для других задач.
Геоцентрическое изображение сферы. Для различных наблюдателей на Земле удобнее общее изображение сферы (геоцентрическое). Если поместить центр сферы в центре Земли (см. рис. 1,б), а затем повернуть ось мира PNPS вертикально, получим изображение сферы, справедливое для любого наблюдателя на Земле (рис. 9). Место наблюдателя М проектируется в точку zм, а его меридиан — в меридиан наблюдателя РNzMРS. Аналогично получаются зениты и меридианы других мест, например для Гринвича zГP и РNzГРРS. Для наблюдателя М — полуденная точка экватора Е, от нее отсчитываются tм светила С, как обычно, к W-y. Для Гринвича имеем точку E0 и часовой угол tГР.
Из рис. 9 видно, что долгота места равна разности часовых углов: |
|
tГР—tM=λ |
(3) |
На геоцентрическом изображении сферы нет горизонта, |
поэтому |
применяются полярные координаты при zм, т.е. A и z (см. рис. 9). Помимо приведенных изображений сферы, применяются еще изображения ее на плоскости экватора, горизонта, первого вертикала (как плоские, так и пространственные); онирассматриваютсяприрешениисоответствующихзадач.
16

Графическое преобразование координат на небесной сфере. Переход от одной системы координат к другим можно выполнить различными путями:
–построением сферы и систем координат от руки (приближенное графическое решение);
–с помощью моделей сферы звездного глобуса, планетария, координатных кругов1;
–аналитическим решением сферических треугольников (с любой степенью точности).
Рассмотрим графическое решение задач. Построением сферы называется выполнение перспективного или плоского рисунка ее с нанесением основных линий, точек и координатных систем. В общем случае удобнее применять условное перспективное изображение местной сферы на плоскости меридиана наблюдателя (см. рис. 2).
Меридиан наблюдателя проводится циркулем, остальные кривые наносятся от руки. При построении сферы условимся:
–все большие круги сферы, кроме меридиана наблюдателя, изображать эллипсами;
–полуночную часть меридиана наблюдателя изображать волнистой
линией;
–линии на видимой части сферы, т.е. той, где расположено светило, проводить сплошными, а внутри и позади сферы — пунктирными;
–дуги, равные координатам (или их дополнениям), откладывать на глаз, приблизительно в масштабе основной окружности с точностью до ±5°, как правило, от центра чертежа к его краям.
Порядок построения сферы и преобразования координат рассмотрен в примере 2. Следует иметь в виду, что графическое решение задач на сфере не исчерпывается задачей преобразования координат. В дальнейшем будут введены движения светил и графическое приближенное решение поможет понять особенности этих движений.
1 Приборы и машины для преобразования координат рассмотрены в § 91.
17
Пример 2. Построить сферу для ϕ=40°S, нанести светило по t=295°W и
δ=50°S. Определить h и А.
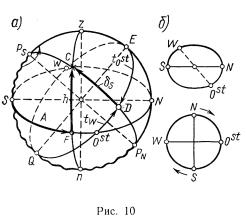
Решение. Проводим окружность R=4 см. Вертикальный диаметр ее изобразит отвесную линию zn, горизонтальный — полуденную линию NS (рис. 10). Однако прежде чем нанести точки N и S, следует определить, какой стороной к наблюдателю должна быть повернута сфера. Указанием служит часовой угол или рассматриваемое явление, например заход светила на W-e. На рис. 2 сфера повернута Оst-м к нам, на рис. 4 — W-м. В данном примере t=295°, W=65°О5t, т.е. светило расположено в Ost-й половине сферы и она должна быть повернута к нам Ost-м. Мысленно представляя горизонт NOstSW в виде картушки компаса (рис. 10), поворачиваем ее Оst-м к себе, при этом справа будет N, слева S. От точки S откладываем вверх дугу ϕ=40°S, получаем повышенный полюс Ps, так как в южной широте над горизонтом будет PS. Проводим ось мира PSPN и помечаем полуночную часть PsSnPN. Перпендикулярно PSPN проводим экватор EQ, точка Е его расположена на полуденной части меридиана.
Строим изображение горизонта и экватора в виде эллипсов, их малые полуоси наносим с помощью циркуля. В пересечении эллипсов получаем точки Ost и W. Линии «внутри» и «позади» сферы делаем пунктирными. На этом рисунок сферы закончен. В заключение следует показать стрелкой при полюсе направление вращения (с Ost-a на W). Координата t в практическом (полукруговом) счете откладывается по экватору от точки Е в данном случае к Ost-y. Для удобства отсчета от Ost-a откладывается дуга OstD, равная 90°–65°=25°. Через полученную точку D проводится меридиан PSDPN. По нему от точки D к Ps откладывается δ=50°S, полученная точка С — место светила на сфере. Проводя через нее вертикал zСn, отмечаем дуги FC и SF, которые равны высоте и азимуту светила. На глаз оцениваем эти координаты и записываем: h=45°, А=55° SO=125°.
18
Преобразование координат с помощью моделей сферы. Моделью сферы и некоторых систем координат является прибор, называемый звездным глобусом. На нем сфера представлена с точки зрения наблюдателя, смотрящего на нее снаружи. Звездный глобус может изображать как местную сферу, так и геоцентрическую, если его вынуть из ящика (см. §42).
Глобус имеет координатные сетки, разделенные на градусы, поэтому преобразование координат осуществляется установкой глобуса и его координатных кругов на заданные значения и снятием искомых значений координат приблизительно до 1°. Рекомендуется решить пример 2 на звездном глобусе.
Другой имитацией сферы является проекционная установка, называемая планетарием. В нем сфера рассматривается изнутри так, как виден небесный свод в натуре. В связи с этим изображения созвездий на глобусе ив планетарии обратны. Планетарий облегчает изучение созвездий и координатных систем, а также позволяет приближенно преобразовывать их (до 3°).
19
