
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •Глава 1. КООРДИНАТИЗАЦИЯ ПРОСТРАНСТВА (ИСТОРИЯ)
- •Координатизация пространства в древнее время
- •Координатизация пространства в новое время
- •Координатизация территории России до ХХ в.
- •Координатизация территории России и СССР в ХХ в.
- •Государственные геодезические сети (плановые)
- •Схемы, программы, этапы развития нивелирных сетей
- •Космическая геодезия и координатные системы
- •Глава 2. МЕТОД И СИСТЕМЫ КООРДИНАТ
- •Общие сведения о координатизации и классификации систем координат
- •Прямоугольные декартовы системы координат
- •Прямоугольные системы координат на плоскости
- •Преобразование плоских прямоугольных координат из одной системы в другую
- •Прямоугольная пространственная система декартовых координат
- •Преобразования пространственных прямоугольных систем координат
- •Преобразования линейных отображений
- •Приведение квадратичной формы общего вида к каноническому
- •Криволинейные координаты
- •Общие сведения о системах криволинейных координат
- •Криволинейные координаты на поверхности
- •Полярные системы координат и их обобщения
- •Пространственная система полярных координат
- •Цилиндрическая система координат
- •Сферическая система координат
- •Полярные координаты на поверхности
- •Глава 3. СИСТЕМЫ КООРДИНАТ, ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИИ
- •Общая классификация систем координат, используемых в геодезии
- •Земные геодезические системы координат
- •Системы полярных координат в геодезии
- •Криволинейные эллипсоидальные системыгеодезических координат
- •Определение эллипсоидальных геодезических координат при раздельном способе определения планового и высотного положений точек земной поверхности
- •Преобразование пространственных геодезических полярных координат в эллипсоидальные геодезические координаты
- •Преобразование референцных систем геодезических координат в общеземные и обратно
- •Пространственные прямоугольные системы координат
- •Связь пространственных прямоугольных координат с эллипсоидальными геодезическими координатами
- •Преобразование пространственных прямоугольных референцных координат в общеземные и обратно
- •Топоцентрические системы координат в геодезии
- •Связь пространственной топоцентрической горизонтной геодезической СК с пространственными полярными сферическими координатами
- •Преобразование топоцентрических горизонтных геодезических координат в пространственные прямоугольные координаты Х, У, Z
- •Системы плоских прямоугольных координат в геодезии
- •Связь плоских прямоугольных координат Гаусса – Крюгера с эллипсоидальными геодезическими координатами
- •Преобразование плоских прямоугольных координат Гаусса – Крюгера из одной зоны в другую
- •Перевычисление плоских прямоугольных координат пунктов локальных геодезических построений в другие системы плоских прямоугольных координат
- •Глава 4. СИСТЕМЫ КООРДИНАТ,ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИЧЕСКОЙ АСТРОНОМИИ И КОСМИЧЕСКОЙ ГЕОДЕЗИИ
- •Системы координат сферической астрономии
- •Системы отсчета в космической геодезии
- •Звездные (небесные) инерциальные геоцентрические экваториальные координаты
- •Гринвичская земная геоцентрическая система пространственных прямоугольных координат
- •Топоцентрические системы координат
- •Глава 5. КООРДИНАТИЗАЦИЯ ОКРУЖАЮЩЕГО ПРОСТРАНСТВА В НАЧАЛЕ ХХI ВЕКА В РОССИИ
- •Системы государственных геодезических координат в начале ХХI в.
- •Построение Государственной геодезической сети
- •СПИСОК ЛИТЕРАТУРЫ
- •ПРИЛОЖЕНИЕ 1. РЕШЕНИЕ ПРЯМОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ В ПРОСТРАНСТВЕ
- •ПРИЛОЖЕНИЕ 2. РЕШЕНИЕ ОБРАТНОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ В ПРОСТРАНСТВЕ
- •ПРИЛОЖЕНИЕ 3. ПРЕОБРАЗОВАНИЕ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ B, L, H В ПРОСТРАНСТВЕННЫЕ ПРЯМОУГОЛЬНЫЕ Х, У, Z
- •ПРИЛОЖЕНИЕ 4. ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВЕННЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ Х, У, Z В ГЕОДЕЗИЧЕСКИЕ B, L, H
- •ПРИЛОЖЕНИЕ 5. ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВЕННЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ Х, У, Z СК-42 В КООРДИНАТЫ СИСТЕМЫ ПЗ-90
- •ПРИЛОЖЕНИЕ 6. ПРЕОБРАЗОВАНИЕ РЕФЕРЕНЦНОЙ СИСТЕМЫ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ B, L, H В СИСТЕМУ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ПЗ-90 B0, L0, H0
- •ПРИЛОЖЕНИЕ 7. ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВЕННЫХ ПОЛЯРНЫХ КООРДИНАТ СИСТЕМЫ S, ZГ, A В ТОПОЦЕНТРИЧЕСКИЕ ГОРИЗОНТНЫЕ ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ ХТ, УТ, ZТ
- •ПРИЛОЖЕНИЕ 8. ПРЕОБРАЗОВАНИЕ ТОПОЦЕНТРИЧЕСКИХ ГОРИЗОНТНЫХ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ХТ, УТ, ZТ В ПОЛЯРНЫЕ ПРОСТРАНСТВЕННЫЕ КООРДИНАТЫ – S, ZГ, A
- •ПРИЛОЖЕНИЕ 9. ПРЕОБРАЗОВАНИЕ ТОПОЦЕНТРИЧЕСКИХ ГОРИЗОНТНЫХ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ХТ, УТ, ZТ В ПРОСТРАНСТВЕННЫЕ ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ X, У, Z
- •ПРИЛОЖЕНИЕ 10. ПРЕОБРАЗОВАНИЕ ЭЛЛИПСОИДАЛЬНЫХ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ B, L В ПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ ГАУССА – КРЮГЕРА Х, У
- •ПРИЛОЖЕНИЕ 11. ПРЕОБРАЗОВАНИЕ ПЛОСКИX ПРЯМОУГОЛЬНЫX КООРДИНАТ ГАУССА – КРЮГЕРА X, Y В ЭЛЛИПСОИДАЛЬНЫЕ ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ B, L
B = ϕ − ξ; |
|
|
|
|
(3.2) |
|
|
|
L = λ −η secϕ, |
|
|
|
|
|
где ξ и η – проекции полного уклонения отвесных линий, соответственно, на плоскость меридиана и первого вертикала.
3.2.3.Определение эллипсоидальных геодезических координат при раздельном способе определения планового и высотного положений точек земной поверхности
При построении наземных геодезических сетей, предназначенных для определения положения точек физической поверхности Земли, во многих странах мира принят принцип раздельного определения планового и высотного положения. С целью определения планового положения точки на земной поверхности строятся специальные (плановые) геодезические сети в виде триангуляции, трилатерации, полигонометрии. Для определения высотного положения точки, строятся сети нивелирования.
Обработка наземных плановых геодезических сетей должна осуществляться на координатной поверхности, в качестве которой, как уже отмечалось выше, в настоящее время используется эллипсоид вращения. Поэтому в геодезии возникает задача – по результатам (элементам) геодезических сетей (сторонам, углам, азимутам) определить геодезические координаты B, L и азимуты А точек поверхности земного эллипсоида.
Эта задача в геодезии получила специальное название – прямая геодезическая задача на эллипсоиде, хотя с точки зрения преобразования координат ее можно трактовать как задачу преобразования эллипсоидальных полярных координат точки в геодезические.
Существует большое разнообразие способов решения этой задачи на эллипсоиде, основанных на интегрировании дифференциальных уравнений (2.62) в системе геодезических координат. Не останавливаясь здесь на анализе этих методов, их достоинствах и недостатках, приведем без вывода один из наиболее простых в практическом отношении, который в геодезической
литературе называется «способом со средними аргументами» и позволяет определить координаты с точностью 0.0003" при S ≤ 60 км.
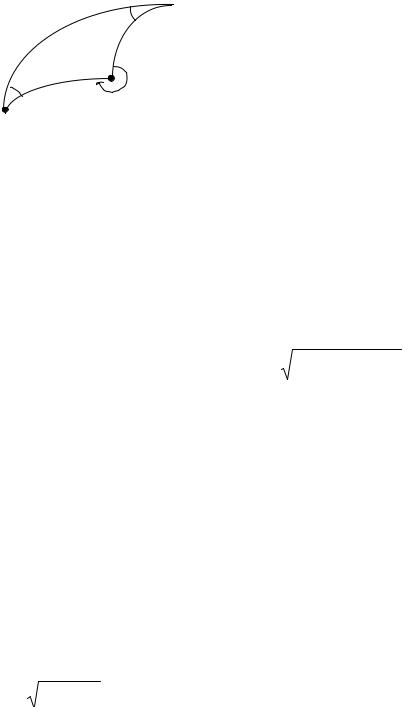
Прямая геодезическая задача на эллипсоиде
На рис. 3.3 дана геометрическая интерпретация решения прямой
геодезической задачи на эллипсоиде.
Дано: S, А12, В1, L1.
Требуется определить: В2, L2, А21. Решение осуществляется по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 = B1 + |
B; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
L2 = L1 + |
L; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
90 – B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 – B2 |
|
|
|
|
A21 = A12 ± 180 + |
|
|
A; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A12 |
|
|
2 (B2, L2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l''2 |
|
|
|
|
|
a''2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
'' |
|
|
'' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
= b |
1 |
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
; |
|
|
|
|
|||||||
|
|
|
|
|
A21 |
|
|
|
|
|
|
|
|
|
|
|
|
12ρ |
''2 |
|
24 |
ρ |
''2 |
|
|
|
(3.3) |
||||||||||||||||
1 (B1, L1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
'' |
|
|
'' |
|
|
|
|
|
b''2 |
|
|
|
|
|
a''2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
= l |
|
1 − |
|
|
|
|
|
|
|
+ |
|
|
|
|
; |
|
|
|
|
||||||
Рис. 3.3. Геометрия решения |
|
|
|
|
24 |
ρ |
''2 |
|
24ρ |
''2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
геодезической задачи на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
эллипсоиде |
|
|
|
|
|
|
|
|
'' |
= a |
'' |
|
+ |
|
b''2 |
|
+ |
l''2 |
|
|
− |
a''2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12ρ''2 |
|
12 |
ρ |
|
|
24ρ''2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
''2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
b′′ = |
S cos Aср |
ρ′′ |
; |
l′′ |
= |
S sin Aср sec Bρ |
′′ |
; |
a′′ = l′′sin Bср ; |
|
|
|
(3.4) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
M ср |
|
|
Nср |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M |
cp |
= |
a(1 − e2 ) |
; |
N |
cp |
= |
|
|
a |
; W = |
|
1 − e2 sin2 B |
|
|
, |
|
|
|
|
|
|
|
(3.5) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
Wcp3 |
|
|
Wcp |
|
cp |
|
|
|
|
|
|
|
|
|
|
|
|
cp |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в (3.5) а – большая полуось эллипсоида.
Прямая геодезическая задача решается методом итераций.
Обратная геодезическая задача на эллипсоиде
Формулы обратного перехода от геодезических координат B1, L1, B2, L2 к полярным – S, A12 и A21 легко можно получить путем обращения формул (3.3)
B = B2 − B1; L = L2 − L1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
'' |
|
|
|
|
|
|
''2 |
|
|
|
''2 |
sin |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
M cp |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
L |
|
|
|
|
L |
|
Bcp |
|
|
|||||||
P = S cos Acp |
= |
|
|
|
|
|
1 − |
|
|
|
− |
|
|
|
|
|
|
|
|
; |
|
|
|
|||||||
|
|
ρ '' |
|
12ρ ''2 |
|
|
24ρ |
''2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L'' cos B |
|
|
|
|
|
|
|
|
|
|
|
|
L''2 sin2 B |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
N |
cp |
|
|
B |
''2 |
|
|
|
|
|
|||||||||||
Q = S sin Acp |
= |
|
|
|
|
|
cp |
|
|
+ |
|
|
|
− |
|
|
|
cp |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
; |
|
||||||||||
|
|
|
|
ρ '' |
|
|
|
|
24ρ ''2 |
|
|
24ρ ''2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = |
P |
2 |
+ Q |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.6) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Acp |
= arctg |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A12 = Acp − |
A |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A21 = Acp ± 180 + |
A |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом ∆А вычисляется по последней формуле системы (3.3).
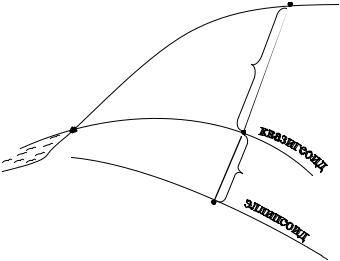
Что касается третьей координаты, геодезической высоты Н (как высоты точки физической поверхности Земли относительно земного эллипсоида), то она определяется как сумма двух слагаемых
H = H γ |
+ζ , |
|
|
|
(3.7) |
||
где Нγ – нормальная высота |
|
||||||
точки Q (рис. 3.4) относительно |
|
||||||
поверхности квазигеоида и ζ – |
|
||||||
высота |
|
квазигеоида |
над |
Нγ |
|||
эллипсоидом. |
|
|
|
|
|||
Нормальная |
высота |
|
Нγ |
|
|||
определяется |
из |
нивелирования |
О |
||||
|
|
|
|
|
|
||
(геометрического |
|
или |
|
||||
тригонометрического) |
точек |
ζ |
|||||
физической |
поверхности Земли, |
а |
|||||
|
|||||||
высота |
ζ |
квазигеоида |
над |
|
|||
эллипсоидом |
определяется |
|
из |
|
|||
специальных |
геодезических |
работ, |
|
||||
получивших |
|
название |
|
||||
нивелирования квазигеоида. |
|
|
|
||||
Но как Нγ, так |
и |
ζ |
Рис. 3.4. Система геодезических высот |
||||
непосредственно |
измерению |
не |
|
||||
подлежат. Из измерений можно получить только их приращения при переходе от одной точки к другой и, если известны для одной из точек Нγi, так и ζ i, то тогда
H γ |
= H |
γ |
+ |
H |
γ |
|
; |
|
|
|
|
|
i+1 |
|
i |
|
|
i,i+1 |
|
|
|
(3.8) |
|
||
ζi+1 = ζi + ζi,i+1 , |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
H iγ,i+1 = |
H i,i+1 |
+ |
|
(γ 0i −γ 0i+1 )H cp + |
(g −γ )cp |
H i,i+1 ; |
(3.9) |
|||||
γ cp |
|
|||||||||||
|
|
|
|
|
|
|
γ cp |
|
|
|||
|
|
|
ϑ'' +ϑ'' |
|
|
|
|
|
|
|||
ζi,i +1 = − |
i |
|
i+1 |
|
S. |
|
|
(3.10) |
|
|||
2ρ'' |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
В этих формулах использованы следующие обозначения:
ϑ – проекции полного уклонения отвесных линий в соответствующих точках на вертикальную плоскость, проходящую через обе точки;
S – расстояние между точками;
∆Нi,i+1 – непосредственно измеренное превышение;
γ 0i = γ э (1+ β sin2 B) |
– нормальное ускорение силы тяжести на эллипсоиде |
|||||
для точки i; |
|
|
|
|
||
(g – |
γ) – аномалия силы тяжести; |
|||||
β = |
5 |
q −α; |
q = |
aω 2 |
||
|
|
|
; |
|||
2 |
γ |
|
||||
|
|
|
э |
|||
а– большая полуось эллипсоида;
α– сжатие эллипсоида;
ω – угловая скорость вращения Земли; γ э = 978031.97 мгл – нормальное ускорение силы тяжести на экваторе (в
системе ПЗ-90).
3.2.4.Преобразование пространственных геодезических полярных координат в эллипсоидальные геодезические координаты
По аналогии с решением задач на эллипсоиде, преобразование пространственных полярных координат в геодезические принято называть прямой геодезической задачей в пространстве, а обратный переход – обратной геодезической задачей в пространстве.
Прямая геодезическая задача в пространстве |
|
|
|
|
|
||||
|
|
|
|
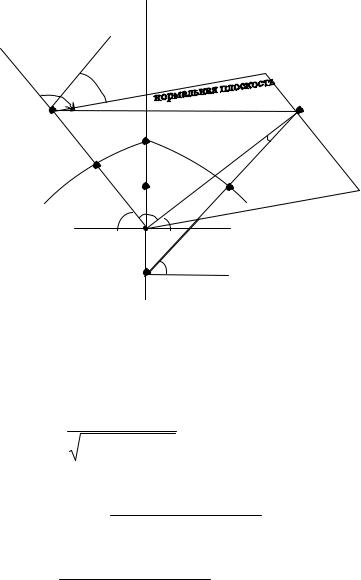
Решение |
|
|
прямой |
||
|
|
11 |
|
геодезической |
задачи |
между |
|||
|
|
|
двумя точками в пространстве |
||||||
|
|
|
|
||||||
|
|
|
|
заключается в том, что по |
|||||
|
15 |
|
|
геодезическим |
|
координатам |
|||
|
|
|
первой точки Q1(В1, L1, Н1) – |
||||||
|
|
|
|
||||||
|
|
17 |
13 |
полюса |
пространственной |
||||
12 |
30 |
|
полярной системы координат, и |
||||||
|
16 |
|
|||||||
|
19 |
|
21 |
сферическим |
|
|
полярным |
||
|
18 |
координатам |
|
второй |
точки |
||||
|
|
|
|
||||||
|
|
σ φ2 |
|
Q2(S, |
Z12, A12) |
вычисляются |
|||
|
27 |
29 |
|
|
|
|
|
|
|
31 L1 = |
26 |
|
22 L = |
геодезические |
|
координаты |
|||
|
24 |
28 |
|
точки Q2(В2, L2, Н2). |
|
||||
|
23 |
|
|
В |
плоском |
треугольнике |
|||
|
|
|
|
Q1n1Q2 (рис. 3.5) угол при |
|||||
|
|
|
|
вершине n1 обозначим через σ, |
|||||
Рис. 3.5. Геометрия прямой и обратной |
сторону Q2n1 |
– через d, а угол, |
|||||||
составленный |
|
отрезком |
d с |
||||||
|
пространственных задач |
|
|||||||
|
плоскостью экватора – через φ2. |
||||||||
|
|
|
|
||||||
Тогда, вычислив радиус кривизны первого вертикала |
|
|
|
|
|||||
Ni = |
a |
(i = 1, 2), |
|
(3.11) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 − e2 sin2 B |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
определяем |
|
|
|
|
|
|
|
|
|
|
|
S sin Z12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ = arctg |
|
; |
|
|
|
|
|
|
|
|
S cos Z12 + N1 |
+ H1 |
|
(3.12 а) |
|
|
|
||
|
|
|
|
|
|
|
|
||
d = S cos Z12 + N1 + H1 . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
cosσ |
|
|
|
|
|
|
|
|
Из точки n1 (рис. 3.5), как из центра, опишем сферу единичного радиуса. Пересекая поверхность сферы плоскостями меридианов точек Q1 и Q2 и
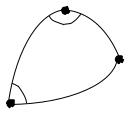
нормальной плоскостью Q1n1Q2, получим сферический треугольник q1pq2 (рис. 3.6), из которого
ϕ2 = arcsin(cosσ sin B1 + sinσ cos B1 cos A12 ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinσ sin A12 |
|
|
|
ctgσ cos B1 |
|
|
|
|
|
|
|
||||||||||||||
L = (L2 |
− L1) = arcsin |
|
|
|
|
|
= arcctg |
|
|
|
|
|
|
|
− ctgA12 sin B1 . |
|||||||||||
|
cosϕ |
2 |
|
|
|
|
sin A |
|
||||||||||||||||||
(3.12 б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
Проектируя отрезки Q2n1 и Q2n2 (рис. 3.5) на |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
p |
ось |
вращения |
эллипсоида |
|
|
и на |
плоскость |
||||||||||||||||||
|
90 – φ2 |
экватора, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
90 – B1 |
ΔL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.13) |
|||
|
q2 |
|
|
B |
= arctg tgϕ |
2 |
+ |
|
|
|
|
|
|
; |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
d cosϕ2 |
|
|
|
|
||||||||
A12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
= e2 |
(N |
|
|
sin B − N |
|
sin B ); |
|||||||
|
|
|
|
|
где |
|
|
|
n n |
2 |
|
2 |
1 |
|||||||||||||
q1 |
σ |
(3.14) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
L; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
L2 = L1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рис. 3.6. Сферический |
|
|
H2 |
= |
|
d cosϕ2 |
− N2. |
|
|
|
|
|
|
|
|
|||||||||||
треугольник единичной |
|
|
|
cos B2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
сферы |
(3.15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Широта В2 по формуле (3.13) определяется |
|||||||||||||||||||||
последовательными приближениями. |
|
В |
первом приближении |
величина |
||||||||||||||||||||||
N 2 sin B2 в выражении (3.14) вычисляется по широте φ2.
Обратная геодезическая задача в пространстве
Решение обратной геодезической задачи между точками в пространстве состоит в том, что по заданным геодезическим координатам B, L, H двух точек определяются полярные координаты второй точки, т. е. расстояние S между полюсом полярной системы координат и второй точкой по прямой, азимут
нормальной плоскости в первой точке А12, и зенитное расстояние Z12 с первой точки на вторую (см. рис. 3.5).
В треугольнике Q2n1n2 угол при вершине Q2 обозначим через γ. Вычислив в соответствии с выражениями (3.11) и (3.14) N1, N2 и отрезок ∆, из треугольника Q2n1n2 находим
|
∆cosB2 |
|
|
|
γ = arctg |
|
|
; |
|
|
+ H1 − ∆sin B2 |
|
||
N2 |
|
(3.16) |
||
d = N2 + H1 − ∆sin B2 ; |
|
|||
|
|
|
|
|
|
cosγ |
|
|
|
2 = B2 − γ ; |
|
|
|
|
∆L = L2 − L1. |
|
|
||
|
|
|||
Далее, решая сферический треугольник q1pq2 (рис. 3.6) относительно σ и А12, получим
