
- •Введение
- •Основные обозначения
- •1. Общие сведения
- •1.1. Ветроволновые воздействия и виды реакции судна на них
- •1.2. Опасности штормового плавания
- •1.2.1. Особенности качки.
- •1.2.2. Проблемы движения против волн
- •1.2.3. Опасности плавания по волне
- •1.2.4. Нагрузки на движительную установку и корпус
- •1.2.5. Основные факторы, влияющие на интенсивность качки
- •Следует также отметить, что с ростом скорости судна ускорения, скорости, угловые и линейные перемещения корпуса, сила ударов волн и интенсивность других неблагоприятных явлений в общем случае увеличиваются.
- •1.3. Мореходность судна и ее обеспечение
- •1.4. Критерии мореходности и режимы штормового плавания
- •1.5. Основные виды контроля мореходности в рейсе
- •2. Характеристика морского волнения
- •2.1. Виды волнения
- •2.2. Регулярное волнение
- •2.3. Нерегулярное двумерное волнение
- •2.4. Нерегулярное трехмерное волнение
- •2.6. Наблюдаемые на судне параметры волнения
- •3.1. Назначение и состав АСКМ
- •3.2. Функциональные возможности систем
- •3.3. Отображение информации в АСКМ
- •4. Датчики информации АСКМ
- •4.1. Устройства для измерения параметров воздействий среды
- •4.1.1. Датчики ветра
- •4.1.2. Определители параметров волнения
- •4.2. Измерители параметров движения судового корпуса
- •4.2.1. Инерциальные датчики угловых параметров качки
- •4.2.2. Инерциальные устройства для измерения линейных параметров качки
- •4.2.3. Комбинированные инерциальные датчики
- •4.2.4. Спутниковые измерители параметров движения корпуса судна
- •4.3. Датчики напряжений корпуса судна и гребного вала
- •4.3.1. Резисторные измерители напряжений
- •SBSG
- •LBSG
- •4.3.2. Волоконно-оптические тензометры
- •4.3.3. Датчики давления
- •4.5.1. Основные виды данных о погоде
- •4.5.2. Компьютерный учет гидрометеорологической информации на судах
- •5. Теоретические основы расчета мореходности
- •5.1. Программные средства для расчетов параметров мореходности
- •5.2.1. Понятие линейной динамической системы
- •5.2.2. Линейная система с детерминированными сигналами
- •5.2.4. Линейная динамическая система с недетерминированными сигналами
- •6. Понятие о методах выбора оптимального плана перехода
- •7. Образцы судовых АСКМ
- •7.1. Система мониторинга параметров мореходности «HULLMOS»
- •7.3. Система для оценки и оптимизации мореходности «VOSS»
- •7.5. Интегрированная морская система поддержки решений «IMDSS»
- •8. Достоинства систем контроля мореходности судна
- •Список литературы
- •6. Понятие о методах выбора оптимального плана перехода
входного, но с другой амплитудой и фазой. Представление сигналов системы суммой гармоник позволяет значительно упростить анализ линейных систем.
Основные виды сигналов динамических систем.
Реальные входные и выходные величины линейной системы описываются двумя видами моделей: детерминированной и недетерминированной (стохастической, вероятностной). Детерминированные сигналы – это функции времени конкретного вида. Недетерминированные сигналы являются случайными процессами, которые только при реализации принимают тот или иной конкретный вид, причем заранее он неизвестен.
5.2.2. Линейная система с детерминированными сигналами
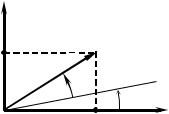
Изображение гармоники на комплексной плоскости. Для упрощения анализа линейной системы ее входные и выходные величины представляются в виде суммы гармоник. Математически гармоника u(t) описывается выражением:
u(t) = u)sin(ωu t + Ψu ) . |
(5.4) |
||
где u – амплитуда гармоники; Ψu – начальная фаза; ωu – |
|||
угловая частота. |
|
|
|
Im |
|
|
|
UIm |
|
|
|
|
u |
ωut |
|
|
|
|
|
0 |
|
Ψu |
Re |
|
URe |
|
|
|
|
|
|
Рис. 5.2. Изображение гармоники на комплексной плоскости
Вместо (5.4) используют также изображение гармоники на плоскости комплексных чисел с действительной ( Re ) и мнимой ( Im ) осями (рис. 5.2). На этой плоскости гармонический сигнал u(t) представляется вектором u длиной u , вращающимся с
149
угловой скоростью ωu относительно начала координат. Изображение гармоники u(t) на плоскости комплексных чисел
обозначим как u(iωu ) , где |
i – мнимая единица. Как любое |
|||
комплексное число, u(iωu ) |
можно записать в алгебраической, |
|||
тригонометрической |
и |
показательной |
формах. |
В |
алгебраическом виде u(iωu ) представляется суммой действительной и мнимой компонент:
u(iωu ) =U Re + i U Im . |
(5.5) |
Тригонометрическая форма u(iωu ) |
получается путем |
замены в (5.5) URe = u)cosϕ, UIm = u)sinϕ , где ϕ = ωu t + Ψu :
|
|
u(iωu ) = u)(cosϕ +isinϕ) . |
(5.6) |
||||||
Для получения показательной формы в (5.6) учитывается, |
|||||||||
что cosϕ = |
1 |
(eiϕ + e−iϕ ) , а sinϕ = |
|
1 |
(eiϕ |
− e−iϕ ) : |
|
||
2 |
|
|
|||||||
|
) iϕ |
) |
|
2i |
|
|
|
||
|
|
i(ω |
t+Ψ ) |
. |
(5.7) |
||||
|
|
u(iωu ) = ue |
= ue |
|
u |
u |
|||
Комплексно-частотное разложение детерминированных сигналов. Допустим, что сигналы на входе и выходе линейной системы являются детерминированными и относятся к функциям, удовлетворяющим условиям Дирихле. С помощью преобразования Фурье любой такой сигнал Z (t) можно
заменить суммой Z(ω) гармоник с частотами от нуля до бесконечности:
∞ |
|
Z (ω) = ∫u)(ω)sin[ωt + Ψ(ω)]. |
(5.8) |
ω=0 |
|
Выражение Z (ω) называется частотным разложением
сигнала Z (t) . Если в (5.8) использовать изображения гармоник на комплексной плоскости, то полученное выражение Z (iω)
будет комплексно-частотным разложением Z (t) −
изображением Z (t) в комплексно-частотной области. Функцию Z (t) в этом случае называют оригиналом Z (iω) . Разложение
150

Z (iω) можно записать в алгебраической или в показательной
форме:
Z (iω) = ZRe (ω) +i ZIm (ω) = Z)(ω) eiϕZ (ω) ; (5.9)
где ϕZ (ω) = ω t + Ψz (ω) ; Z (ω) – амплитуды компонентов
сигнала с частотами от нуля до бесконечности.
Анализируя (5.9), нетрудно установить, что взятие производной от оригинала Z (t) сводится к умножению
изображения Z (iω) на (iω) : |
|
||
|
dZ (t) |
iω Z(iω) . |
(5.10) |
|
dt |
||
|
|
|
|
Представление линейной системы в комплексно-
частотной области. Обозначим комплексно-частотные
изображения входного |
X и выходного Y сигналов в линейной |
|||
системе (рис. 5.1) как |
X (iω) и Y (iω) , а |
связывающий их |
||
оператор, как W (iω) : |
|
|
|
|
Y (iω) =W (iω)X (iω) . |
(5.11) |
|||
X(iω) |
|
Y(iω) |
||
W(iω) |
||||
|
|
|
||
|
|
|
|
|
Рис. 5.3. Линейная система в комплексно-частотной области
В результате получим представление линейной системы в комплексно-частотной области (рис. 5.3). Оператор W (iω)
называется комплексно-частотной передаточной функцией или амплитудно-фазовой частотной характеристикой (АФЧХ)
системы.
Комплексно-частотная передаточная функция системы
определяется как отношение выходной величины системы к входной при условии, что входная величина изменяется по гармоническому закону с различными частотами от 0 до∞:
W (iω) =Wy/ x (iω) = |
Y (iω) |
. |
(5.12) |
|
|||
|
X (iω) |
|
|
Учитывая в выражении (5.2) свойство (5.10), получаем:
151

|
m |
|
|
|
|
∑bk (iω)k |
|
|
|
W (iω) = |
k=0 |
. |
(5.13) |
|
n |
||||
|
|
|
||
|
∑ap (iω) p |
|
|
p=0
Таким образом, при переходе в комплексно-частотную область связь между входным и выходным сигналами становится алгебраической, что упрощает анализ линейной
системы. Учитывая в (5.13), что i2 = −1, и избавляясь от иррациональности в знаменателе, функцию W (iω) запишем в
алгебраической форме: |
|
|
|
W (iω) =WRe (ω) + i WIm (ω) . |
(5.14) |
||
Амплитудно-частотная |
и |
фазово-частотная |
|
характеристики системы. Изображения сигналов системы
выразим в виде (5.8): |
|
|
|
|
) |
|
|
||
|
) |
iϕ |
|
(ω) |
|
iϕy (ω) |
|
||
X (iω) = X (ω)e |
x |
; Y (iω) =Y (ω)e |
. (5.15) |
||||||
|
|
|
|||||||
Здесь X (ω) , Y (ω) |
– амплитуды компонентов входного и |
||||||||
выходного |
сигналов |
|
|
системы; |
ϕx (ω) = ω t + Ψx (ω) ; |
||||
ϕy (ω) = ω t + Ψy (ω) . Учитывая (5.15), передаточную функцию
W (iω) запишем в показательной форме:
|
W (iω) = |
Y (iω) |
= A(ω)eiϕ(ω) . |
(5.16) |
||
|
X (iω) |
|||||
|
|
|
|
|
||
В этом выражении |
|
|
|
|
||
A(ω) = Ay/ x |
(ω) = |
Y)(ω) |
; ϕ(ω) =ϕy (ω) −ϕx (ω) . |
(5.17) |
||
|
|
X (ω) |
|
|
||
Функции |
A(ω) , |
ϕ(ω) |
называют соответственно |
|||
амплитудно-частотной (АЧХ) и фазово-частотной (ФЧХ) характеристиками линейной динамической системы.
Амплитудно-частотная характеристика равняется отношению амплитуды выходной величины к амплитуде входной при условии, что входная величина изменяется по гармоническому закону с различными частотами от 0 до ∞.
152

Фазово-частотная характеристика представляет собой разность фаз выходной и входной величины при условии, что входная величина изменяется по гармоническому закону с различными частотами от 0 до ∞.
Через составляющие WRe (ω) и WIm (ω) передаточной
функции (5.14) АЧХ и ФЧХ линейной системы могут быть найдены по формулам:
A(ω) = |
|
W (iω |
|
= W 2 |
+W |
2 |
; |
(5.18) |
||
|
|
|||||||||
|
|
|
|
|
Re |
|
Im |
|
|
|
ϕ(ω) = arctan |
WIm |
(ω) |
. |
|
|
(5.19) |
||||
WRe |
|
|
|
|||||||
|
|
|
|
|
(ω) |
|
|
|
||
Амплитудно-частотная характеристика является модулем, а фазовая частотная характеристика – аргументом передаточной функции.
5.2.3. Правила получения частотных характеристик линейных систем
Приведем ряд правил, используемых при нахождении частотных характеристик линейных динамических систем.
Правило 1. Чтобы получить выражение комплексночастотной передаточной функции W (iω) по уравнению системы (5.2), необходимо в нем заменить оператор производной на (iω) , обозначения X входного и Y выходного сигналов их изображениями X (iω) , Y (iω) . Затем найти
отношение изображения выходного сигнала к изображению входного и привести к виду (5.14) или (5.16).
После этого по формулам (5.18) и (5.19) можно найти амплитудно-частотную и фазово-частотную характеристики динамической системы.
|
|
|
|
W(iω) |
|
Y(iω) |
||
X(iω) |
|
|
|
|
|
|
|
|
W1(iω) |
|
|
W2(iω) |
|
|
Wn(iω) |
||
|
|
|
|
|
|
|||
|
|
|
||||||
Рис. 5.4. Последовательное соединение звеньев
153
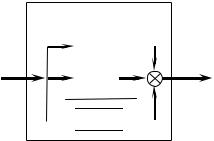
Правило 2. Когда линейная система представляет собой последовательное соединение звеньев (рис. 5.4) с известными
передаточными функциями Wk (iω) , то передаточная функция W (iω) такой системы равна произведению передаточных функций звеньев:
n
W (iω) =W1(iω)×W2 (iω)×...×Wn (iω) = ∏Wk (iω) . (5.20)
|
|
|
|
k=1 |
|
W(iω) |
|||
|
|
|
|
|
X(iω) |
W1(iω) |
|
|
Y(iω) |
|
|
|||
|
|
|
||
W2(iω) |
|
|||
|
|
|
|
|
|
|
|||
 Wn(iω)
Wn(iω) 
Рис. 5.5. Параллельное соединение звеньев
Правило 3. Если линейная система представляет собой параллельное соединение звеньев (рис. 5.5) с известными
передаточными функциями Wk (iω) , то передаточная функция W (iω) такой системы равна сумме передаточных функций звеньев:
n
W (iω) =W1 (iω) +W2 (iω) +... +Wn (iω) = ∑Wk (iω) . (5.21)
k =1
В заключение следует отметить, что достоинством частотных характеристик является и то, что они могут быть определены экспериментальным путем. При этом необязательно знать математическое описание системы.
154
