127

x(t −τ ) = x(t −τ ) .

Перечисленные свойства могут быть легко доказаны с помощью формулы (13.1).

В общем случае среднее значение произведения двух функций времени не равно произведению их средних значений:

x(t ) y(t) ¹ x(t ) y(t ) .

Однако если x(t ) и y(t ) имеют малый уровень пульсаций и изменяются относительно медленно, то можно пользоваться приближенным равенством:

Поскольку средние значения токов и напряжений удовлетворяют условиям линейности и инвариантности во времени, для них справедливы законы Кирхгофа:

åik = 0;

k

åuk = 0 .

k

Компонентные уравнения линейных элементов для средних значений аналогичны уравнениям для мгновенных значений.

Для резистора u (t ) = Ri (t ) .

Для индуктивного элемента u (t) = L didt(t) .

Компонентное уравнение емкостного элемента i (t ) =C dudt(t) .

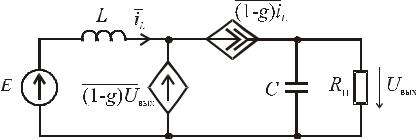
Нелинейным элементам, а также элементам, изменяющимся во времени соответствуют схемы замещения на основе управляемых источников. В качестве иллюстрации на рис. 13.1 показан повышающий импульсный регулятор, а на рис. 13.2 – схема замещения для средних значений.

128 Рис. 13.1

Рис. 13.2

В схеме на рис. 13.2 g(t ) – функция переключения.

Рассмотренный метод, заключающийся в замене каждого элемента моделью для средних значений, называют методом прямого усреднения (in-place averaging).

Достоинство метода заключается в том, что непрерывную модель можно анализировать с помощью программ схемотехнического моделирования, таких как Pspice или Multisim.

3. Уравнения состояния электрических цепей

В последние годы для расчета систем с периодической коммутацией предложено несколько методов. Одним из них является метод усредненных переменных состояния. Он широко используется для исследования характеристик импульсных преобразователей.

Рассмотрим сначала основные положения метода переменных состояния применительно к цепям с непрерывными токами и напряжениями.

Поведение электрической цепи описывается в общем случае системой дифференциальных уравнений. С помощью подстановок и замены переменных эту систему уравнений можно преобразовать к одному дифференциальному уравнению n-го порядка. Как правило, порядок уравнения равен суммарному числу индуктивных и емкостных элементов: n= nL + nC . Однако более рационально записывать систему дифференциальных уравнений в нормальной форме (форме Коши).

Уравнения в форме Коши состоят из уравнений первого порядка, разрешенных относительно первой производной одной из переменных. В левой части каждого уравнения записывают производную, а в правой –

129

функции переменных цепи и напряжений и токов независимых источников.

В матричной форме уравнения состояния имеют вид:

[X(t)] =[A][X(t)] + [B][U (t)] .

Квадратную матрицу [A] называют матрицей параметров схемы, а

[B]– матрицей параметров входного воздействия.

Вкачестве примера запишем уравнения состояния последовательной RLC-цепи (рис. 13.3):

didtL = − RL iL (t) − L1uC (t) + L1e(t), dudtC = C1 iL (t) .

Рис. 13.3

Матрица параметров схемы

линейную комбинацию вектора переменных состояния и вектора входных воздействий:

[Y (t)] = [C][ X (t)] + [D][U (t )].

130

Матрицы [C] и [D] зависят от конфигурации и параметров цепи. Например, если компонентами вектора [Y (t )] являются напряжения uL и uR, они находятся с помощью уравнений

uL (t) = −RiL (t) − uC (t) + e(t) ;

uR (t ) = RiL (t) .

В матричной форме

Существует несколько причин, по которым дифференциальные уравнения электрической цепи целесообразно представлять в форме уравнений состояния. Во-первых, уравнения состояния можно записать как для линейных, так и для нелинейных цепей. Во-вторых, не всегда можно получить аналитическое решение нелинейного дифференциального уравнения, а численные методы решения ориентированы на уравнения, записанные в нормальной форме. Наконец, в-третьих, матричная форма уравнений состояния не зависит от порядка цепи.

4. Метод усредненного пространства состояний

Метод усредненного пространства состояний основан на том факте, что любой широтно-импульсный преобразователь представляет систему с двумя или более состояниями. В каждом из двух положений ключа система линейна, и уравнения состояния могут быть записаны обычным путем. Переменными состояния являются токи индуктивных и напряжения емкостных элементов. В матричной форме записи уравнения состояния импульсной системы имеют вид

[X ] =[A]1 [X ] + [B]1 [U ]

[X ] =[A]2 [X ] + [B]2 [U ]

Здесь [A]1 , [A]2 , [B]1 , [B]2 – системные матрицы для каждого из двух состояний ключей.

Основной момент в методе усредненных переменных состояния состоит в замещении двух уравнений состояния одним эквивалентным уравнением

[X ] =[A][X ] +[B][U ],

133

В настоящее время получил распространение вариант метода, называемый прямым усреднением (direct circuit averaging). Анализируемая цепь представляется схемой замещения, в которой каждый элемент заменен усредненной моделью. Компонентные уравнения индуктивного, емкостного и резистивного элементов выполняются как для мгновенных, так и для средних значений переменных. Поэтому модели этих элементов описываются такими же уравнениями, как и сами элементы.

5.Выводы

1.Анализ и проектирование импульсных источников являются весьма трудоемкими. Причина в том, что традиционные методы анализа непрерывных цепей для таких систем неприменимы.

2.Основными аналитическими методами расчета импульсных преобразователей являются метод усреднения и метод переменных состояния.