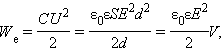Работа силы (сил) над одной точкой
Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:
![]()
Здесь
точкой обозначено скалярное
произведение, ![]() — вектор
перемещения; подразумевается, что
действующая сила
— вектор
перемещения; подразумевается, что
действующая сила ![]() постоянна
в течение всего того времени, за которое
вычисляется работа.
постоянна
в течение всего того времени, за которое
вычисляется работа.
В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки:
![]()
(подразумевается
суммирование по кривой, которая является
пределом ломаной, составленной из
последовательных перемещений ![]() если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
если
вначале считать их конечными, а потом
устремить длину каждого к нулю).
Если существует зависимость силы от координат, интеграл определяется следующим образом:
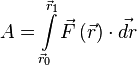 ,
,
где ![]() и
и ![]() — радиус-векторы начального
и конечного положения тела соответственно.
— радиус-векторы начального
и конечного положения тела соответственно.
Следствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю
Кинетическая энергия
Рассмотрим систему, состоящую из одной материальной точки, и запишем второй закон Ньютона:
![]()
![]() —
есть
равнодействующая всех сил,
действующих на тело. Скалярно
умножим уравнение
на перемещение материальной
точки
—
есть
равнодействующая всех сил,
действующих на тело. Скалярно
умножим уравнение
на перемещение материальной
точки ![]() .
Учитывая, что
.
Учитывая, что ![]() ,
получим:
,
получим:
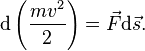
Если система
замкнута, то есть внешние по отношению
к системе силы отсутствуют, или
равнодействующая всех сил равна нулю,
то  ,
а величина
,
а величина
![]()
остаётся постоянной. Эта величина называется кинетической энергией материальной точки. Если система изолирована, то кинетическая энергия является интегралом движения.
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
![]()
где:
![]() —
масса
тела
—
масса
тела
![]() —
скорость центра
масс тела
—
скорость центра
масс тела
![]() — момент
инерции тела
— момент
инерции тела
![]() — угловая
скорость тела.
— угловая
скорость тела.
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
![]()
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
Неконсервативными(диссипативными) силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными
Если тело перемещается
вблизи поверхности Земли, то на него
действует постоянная по величине и
направлению сила тяжести ![]() Работа
этой силы зависит только от вертикального
перемещения тела. На любом участке пути
работу силы тяжести можно записать в
проекциях вектора перемещения
Работа
этой силы зависит только от вертикального
перемещения тела. На любом участке пути
работу силы тяжести можно записать в
проекциях вектора перемещения![]() на
осьOY,
направленную вертикально вверх:
на
осьOY,
направленную вертикально вверх:
|
ΔA = Fт Δs cos α = –mgΔs y, |
где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY (рис. 1.19.3), то сила тяжести совершила работу
|
A = –mg (h2 – h1) = –(mgh2 – mgh1). |
Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
|
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
|
Потенциальная энергия Eр зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготения). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид :
|
где M – масса Земли, G – гравитационная постоянная.
Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
|
|
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
|
Потенциальная энергия - часть общей механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле (например, гравитационном; см. Поля физические) . Численно П. э. системы в данном её положении равна: работе, которую произведут действующие на систему силы при перемещении системы из этого положения в то, где П. э. условно принимается равной нулю (П = 0). Из определения следует, что понятие П. э. имеет место только для консервативных систем, т. е. систем, у которых работа действующих сил зависит только от начального и конечного положения системы. Так, для груза весом Р, поднятого на высоту h, П. э. будет равна П = Ph (П = 0 при h = 0); для груза, прикрепленного к пружине, П = 0,5сl2, где l — удлинение (сжатие) пружины, с — её коэффициент жёсткости (П = 0 при l = 0); для двух частиц с массами m1 и m2, притягивающихся по закону всемирного тяготения, П = —fm1m2/r, где f — гравитационная постоянная, r — расстояние между частицами (П = 0 при r = ¥); аналогично определяется П. э. двух точечных зарядов e1 и e2.
Первая — обобщенная форма: количество затраченной работы равно количеству полученной энергии. Вторая — частная в современной терминологии формулируется так: сумма кинетической и потенциальной энергии в замкнутой системе остается всегда постоянной.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергиител, взятому с противоположным знаком:
|
A = –(Eр2 – Eр1). |
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
|
|
Следовательно
|
|
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
|
|
Обратим
внимание на то, что сила ![]() натяжения
нити всегда перпендикулярна скорости
тела; поэтому она не совершает работы.
натяжения
нити всегда перпендикулярна скорости
тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
|
|
Из этих соотношений следует:
|
|
Центростремительное
ускорение в нижней точке создается
силами ![]() и
и![]() направленными
в противоположные стороны:
направленными
в противоположные стороны:
|
|
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
|
F = 6mg. |
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.20.2).
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
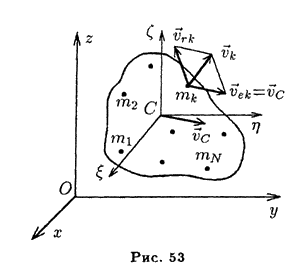
При сложном движении тела кинетическую энергию вычисляют при помощи следующей теоремы (теоремы Кёнига): кинетическая энергия механической системы равна кинетической энергии ее центра масс в предположении, что в нем сосредоточена масса всей системы, плюс кинетическая энергия системы в ее относительном движении по отношению к осям Кёнига.
Докажем
эту теорему. Пусть скорости материальных
точек системы относительно неподвижной
системы координат Oxyz равны соответственно v1,
v2,
…, vn.
Введем вспомогательную систему координат
![]() c
началом в центре масс системы С и осями,
движущимися поступательно вместе
с центром масс (рис.
53; на рисунке оси
c
началом в центре масс системы С и осями,
движущимися поступательно вместе
с центром масс (рис.
53; на рисунке оси ![]() выбраны
соответственно параллельными осям
выбраны
соответственно параллельными осям ![]()
![]() ).
Как и для твердого тела эти вспомогательные
оси называются осями Кёнига. Теперь
движение каждой точки системы можно
рассматривать как движение сложное, в
котором переносным является движение
осей Кёнига, а относительным — движение
точки по отношению к осям Кёнига. Для
скоростей v1,
v2,
…, vn,
являющихся абсолютными скоростями, на
основании теоремы сложения скоростей
можем записать:
).
Как и для твердого тела эти вспомогательные
оси называются осями Кёнига. Теперь
движение каждой точки системы можно
рассматривать как движение сложное, в
котором переносным является движение
осей Кёнига, а относительным — движение
точки по отношению к осям Кёнига. Для
скоростей v1,
v2,
…, vn,
являющихся абсолютными скоростями, на
основании теоремы сложения скоростей
можем записать:
![]()
Здесь
учтено, что при
переносном поступательном движении переносные
скорости всех точек одинаковы и равны
скорости начала подвижной системы
координат (в данном случае —
скорости ![]() центра масс).
Подставляя это выражение в формулу
для кинетической энергии системы,
получаем:
центра масс).
Подставляя это выражение в формулу
для кинетической энергии системы,
получаем:
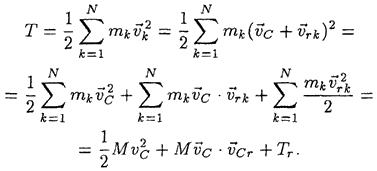
В
этой формуле 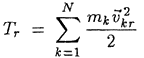 — кинетическая энергия
системы в относительном движении по
отношению к осям Кёнига;
— кинетическая энергия
системы в относительном движении по
отношению к осям Кёнига; ![]() —
относительная скорость центра масс по
отношению к этим же осям. В силу выбора
подвижных осей
—
относительная скорость центра масс по
отношению к этим же осям. В силу выбора
подвижных осей ![]() и из полученного равенства следует
и из полученного равенства следует
![]()
что и доказывает теорему.
При
помощи теоремы Кёнига получим формулу
для вычисления кинетической энергии при
плоскопараллельном движении. Примем
за полюс центр масс тела,
оси Кёнига ![]() расположим
в плоскости движения, ось
расположим
в плоскости движения, ось ![]() —
перпендикулярно этой плоскости. Тогда
плоскопараллельное движение представится
как сумма поступательного движения вместе
с осями Кёнига (переносное движение)
и вращения вокруг оси
—
перпендикулярно этой плоскости. Тогда
плоскопараллельное движение представится
как сумма поступательного движения вместе
с осями Кёнига (переносное движение)
и вращения вокруг оси ![]() с
угловой скоростью тела
w
(относительное движение).
Так как относительное движение
вращательное, слагаемое
с
угловой скоростью тела
w
(относительное движение).
Так как относительное движение
вращательное, слагаемое ![]() в
формуле Кёнига определяется по формуле
в
формуле Кёнига определяется по формуле ![]() ,
где
,
где ![]() — момент инерции тела
относительно оси Кёнига, перпендикулярной
плоскости движения. После подстановки
этого значения в формулу Кёнига, получаем
— момент инерции тела
относительно оси Кёнига, перпендикулярной
плоскости движения. После подстановки
этого значения в формулу Кёнига, получаем
![]()
По этой формуле и следует вычислять кинетическую энергию тела при плоскопараллельном движении.
Для
замкнутой системы тел момент внешних
сил всегда равен нулю, так как внешние
силы вообще не действуют на замкнутую
систему.
Поэтому ![]() ,
то есть
,
то есть
![]() или
или ![]()
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени. Это один из фундаментальных законов природы. Аналогично для замкнутой системы тел, вращающихся вокруг оси z:
![]() отсюда
отсюда ![]() или
или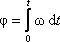 .
.
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Работой A,
совершаемой постоянной силой ![]() называется
физическая величина, равная произведению
модулей силы и перемещения, умноженному
на косинус угла α между векторами
силы
называется
физическая величина, равная произведению
модулей силы и перемещения, умноженному
на косинус угла α между векторами
силы![]() и
перемещения
и
перемещения![]() :
:
|
Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
Если проекция ![]() силы
силы![]() на
направление перемещения
на
направление перемещения![]() не
остается постоянной, работу следует
вычислять для малых перемещений Δsi и
суммировать результаты:
не
остается постоянной, работу следует
вычислять для малых перемещений Δsi и
суммировать результаты:
|
|
Это сумма в пределе (Δsi → 0) переходит в интеграл.
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x)
Примером силы, модуль которой
зависит от координаты, может служить
сила упругости пружины, подчиняющаяся закону
Гука. Для того, чтобы
растянуть пружину, к ней нужно приложить
внешнюю силу ![]() модуль
которой пропорционален удлинению
пружины
модуль
которой пропорционален удлинению
пружины
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
|
|
Этой же формулой выражается
работа, совершенная внешней силой при
сжатии пружины. В обоих случаях работа
упругой силы ![]() равна
по модулю работе внешней силы
равна
по модулю работе внешней силы![]() и
противоположна ей по знаку.
и
противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
|
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
|
|
Работа момента сил,
действующего на тело, вращающееся вокруг
неподвижной оси ![]() ,
где
,
где ![]() —
момент силы,
—
момент силы, ![]() —
угол поворота.
В общем случае
—
угол поворота.
В общем случае 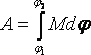 .
Совершенная
над телом работа переходит
в его кинетическую энергию.
.
Совершенная
над телом работа переходит
в его кинетическую энергию.
В общем случае, работа переменной силы,
действующей на тело, движущееся по
криволинейной траектории 
Электричество
Напряженность и потенциал электростатического поля, Кулоновское поле точечного заряда 33
Теорема Гаусса для вектора эл. поля 35
Циркуляция вектора напряженности электростатического поля. Потенциал, связь напряженности и потенциала поля 37
Электрический диполь 38
Диполь в электрическом поле 42
Диэлектрики в электрическом поле, поляризация, коэф. Относительной диэлектрической проницаемости 45
Вектор электрического смещения. Теорема Гаусса для вектора смещения 49
Электроемкость. Конденсаторы 61
Энергия и плотность энергии электростатического поля. Энергия системы точечных зарядов 63
Проводники в эл. поле. Индуцированные заряды, экранировка 69
Магнетизм
Силы Ампера и Лоренца, определение вектора маг. Индукции 72
Магнитное поле. Закон Био-Савара-Лапласа 76
Теорема Гаусса для вектора индукции маг. Поля 82
Контур с током в маг. поле, маг. момент, маг. диполь 82
Токи намагничивания и токи проводимости в веществе. Вектор намагниченности и вектор напряженности 87
Теоремы о циркуляции для вектора напряженности м.п. 88
Понятия о диа- пара- и ферромагнетиках, коэф. Относительной маг. проницаемости вещества. 89
Электричество
Электрическое
поле
– силовое поле, посредством которого
взаимодействуют электрические заряды.
Электростатическое
поле
– поле, создаваемое неподвижными
электрическими зарядами.
Пробный
точечный положительный заряд
(Q0)
– заряд, используемый для обнаружения
и опытного исследования электростатического
поля и не искажающий исследуемое поле
(не вызывает перераспределения зарядов,
создающих поле).
Напряженность
электростатического поля
Напряженность
поля точечного заряда
Скалярная
форма записи
Направление
вектора Е совпадает с направлением
силы, действующей на положительный
заряд. Если
поле создается положительным зарядом,
то вектор Е направлен от заряда во
внешнее пространство; если поле создается
отрицательным зарядом, то вектор Е
направлен к заряду.
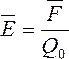 (н/Кл).
(н/Кл).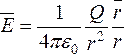 (векторная
запись)
(векторная
запись) .
.
Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа Работа консервативных сил совершается за счет убыли потенциальной энергии.
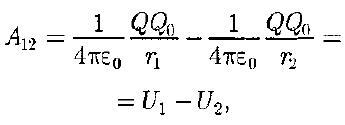

Потенциальная энергия U определяется с точностью до постоянной С. Значение постоянной обычно выбирается так, чтобы при удалении заряда на бесконечность (r → ∞) потенциальная энергия обращается в нуль ( U = 0), тогда С = 0 и потенциальная энергия заряда Qo, находящегося в поле заряда Q на расстоянии r от него, равна

Если поле создается системой n точечных зарядов Q1, Q2,..., Qn, то работа электростатических сил, совершаемая над зарядом Qo, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Qo, находящегося в этом поле, равна сумме потенциальных энергий Ui каждого из зарядов:

Из формул вытекает, что отношение U/Qo не зависит от Qo и является энергетической характеристикой электростатического поля, называемой потенциалом:
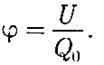
Потенциал поля, создаваемого точечным зарядом Q, равен

Тогда
![]()
С другой стороны
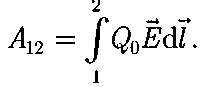
Следовательно:

Если перемещать заряд Qо из произвольной точки за пределы поля, т. е. на бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля равна
![]()
Откуда

Потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля на бесконечность.
Единица потенциала и разности потенциалов — вольт (В): 1 В — потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.
Потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
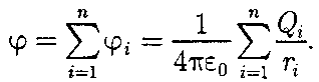
Теорема Гаусса для электростатического поля:
поток вектора напряженности поля через любую замкнутую поверхность равен полному заряду внутри этой поверхности, деленному на e0 .
В интегральной форме:
 ,
(23.15)
,
(23.15)
где q − суммарный заряд внутри поверхности S.
Их расположение внутри поверхности не играет никакой роли. Заряды, расположенные вне замкнутой поверхности S не вносят вклада в поток F, ибо, сколько силовых линий входит в замкнутую поверхность, столько этих линий и выходит.
Рассмотрим некоторые важные примеры.
а). Поле бесконечной равномерно заряженной плоскости.
Пусть
плоскость заряжена равномерно с
поверхностной плотностью заряда s
(Кл/м2).
Вектор напряженности электрического
поля перпендикулярен плоскости и нормали
![]() к
ней.
к
ней.
Поскольку
поле вверх или вниз одинаково, а поток
через боковую поверхность равен 0 (из-за
того, что вектор
![]() перпендикулярен
нормали к этой поверхности), имеем:
перпендикулярен
нормали к этой поверхности), имеем:
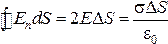 .
.
Сократим на ΔS:
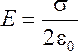 .
(23.16)
.
(23.16)
б) Поле бесконечного равномерно заряженного цилиндра (нити) с линейной плотностью заряда t
В силу симметрии вектор напряженности электрического поля направлен радиально, т. е. перпендикулярно к оси нити (см рис.).
Следовательно, для определения поля добно выбрать цилиндрическую поверхность с осью, совпадающей с осью нити. Используя теорему Гаусса, имеем:
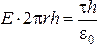 .
.
где h − длина выбранной цилиндрической поверхности.
Если цилиндр радиуса R имеет поверхностную плотность заряда s, а внутри его зарядов нет, то получаем:
 (23.18)
(23.18)
в) Поле равномерно заряженного шара радиуса R
Пусть имеем шар радиуса R, заряженный равномерно по всему объему с плотностью заряда r. Из соображений симметрии электрическое поле направлено радиально
. Сначала находим поле вне шара. Для этого окружаем шар сферой радиуса r > R и находим поток вектора напряженности электрического поля, который по теореме Гаусса равен полному заряду внутри сферы:
 .
(23.19)
.
(23.19)
Отсюда получим поле, совпадающее с полем точечного заряда:
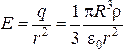 .
(23.20)
.
(23.20)
Для определения поля внутри шара выбираем соответствующую поверхность: сферу внутри шара r < R. Тогда по теореме Гаусса
 .
.
Отсюда получим поле внутри равномерно заряженного шара:
 .
(23.21)
.
(23.21)
Соотношение (3-8) легко записать в векторном виде, поскольку поле внутри шара направлено по радиусу:
 .
(23.22)
.
(23.22)
Работа,
совершаемая при перемещении электрического
заряда во внешнем электростатическом
поле по любому замкнутому пути L, равна
нулю, т.е.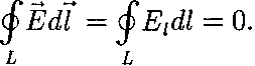
Этот интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.


Определение.
Электрическим диполем называется
система двух одинаковых по величине и
противоположных по знаку зарядов
![]() и
и![]() ,
расстояние
,
расстояние![]() между
которыми много меньше расстояния до
тех точек, в которых определяется
электрическое поле системы. Осью диполя
называется прямая, проходящая через
оба заряда.
между
которыми много меньше расстояния до
тех точек, в которых определяется
электрическое поле системы. Осью диполя
называется прямая, проходящая через
оба заряда.
Потенциал
поля системы зарядов
![]() и
и
![]() находится
в любой точке в соответствии с (1.24) и
рис. 1.13 как
находится
в любой точке в соответствии с (1.24) и
рис. 1.13 как
 (1.35)
(1.35)
Так
как
![]() ,
то приближенно можно положить
,
то приближенно можно положить
 (1.36)
(1.36)
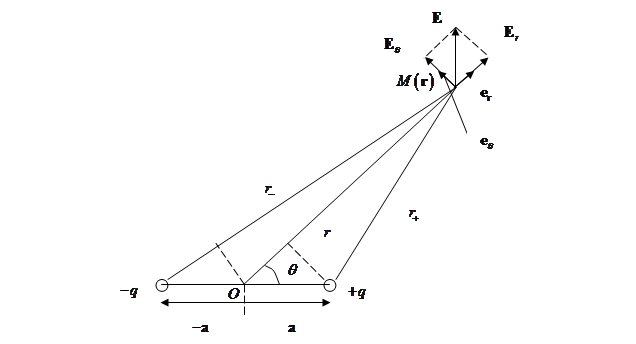
Рис.
1.13. К расчету электрического поля диполя,
![]() ,
,
точка
![]() -
начало системы координат
-
начало системы координат
Отсюда
![]() Кроме
того, при
Кроме
того, при![]() имеем:
имеем:![]() .
Вместо (1.35) приближенно получаем
.
Вместо (1.35) приближенно получаем
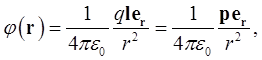 (1.37)
(1.37)
где
![]() -электрический моментдиполя,
-электрический моментдиполя,
![]() (1.38)
(1.38)
Вектор
![]() направлен
вдоль оси диполя от отрицательного
заряда к положительному (см. рис. 1.14).
направлен
вдоль оси диполя от отрицательного
заряда к положительному (см. рис. 1.14).

Рис. 1.14. Электрический момент диполя
Из
(1.38) видно, что поле диполя определяется
его электрическим моментом. Потенциал
поля диполя убывает с расстоянием от
него по закону
![]() ,
то есть быстрее, чем потенциал точечного
заряда (
,
то есть быстрее, чем потенциал точечного
заряда (![]() ).
Поле диполя обладает осевой симметрией
относительно оси диполя. Так как
).
Поле диполя обладает осевой симметрией
относительно оси диполя. Так как![]() ,
то в полярной системе координат
,
то в полярной системе координат![]() выражение
(1.37) запишется как
выражение
(1.37) запишется как
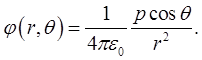 (1.39)
(1.39)
В полярной системе координат оператор «набла» записывается как
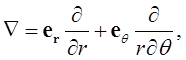 (1.40)
(1.40)
где
![]() и
и![]() -
базисные векторы данной системы координат
(см. рис. 1.13).
-
базисные векторы данной системы координат
(см. рис. 1.13).
Подставим (1.40) в (1.33), получим выражение напряженности электрического поля диполя через потенциал в полярных координатах:
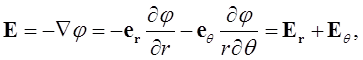 (1.41)
(1.41)
где с учетом (1.39)
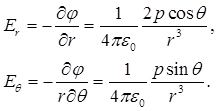 (1.42)
(1.42)
Модуль напряженности поля диполя
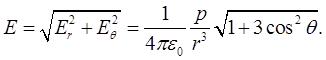 (1.43)
(1.43)
Напряженность
поля диполя убывает с расстоянием от
него по закону
![]() ,
то есть быстрее, чем напряженность поля
точечного заряда (
,
то есть быстрее, чем напряженность поля
точечного заряда (![]() ).
).
Картина
силовых линий электрического поля
системы зарядов
![]() и
и
![]() показана
на рис. 1.15.
показана
на рис. 1.15.
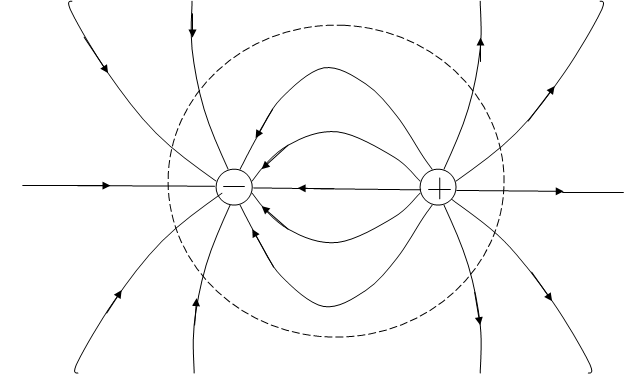
Рис.
1.15. Картина силовых линий электрического
поля системы зарядов
![]() и
и
![]() ,
формулы (1.40), (1.42) и (1.43) для поля диполя
приближенно справедливы
,
формулы (1.40), (1.42) и (1.43) для поля диполя
приближенно справедливы
вне
сферы (пунктирная линия) достаточно
большого радиуса
![]() ,
,
где
![]() -
расстояние между зарядами
-
расстояние между зарядами
Плоскость
![]() (перпендикулярна
оси диполя и проходит через его середину)
является эквипотенциальной:
(перпендикулярна
оси диполя и проходит через его середину)
является эквипотенциальной:![]() .
.
Теперь изучим поведение диполя во внешнем электрическом поле. Пусть диполь помещен в однородное электрическое поле (см. рис. 1.16).
На диполь действует момент электрической силы
![]() (1.44)
(1.44)
где
![]() ,
,![]() ,
,![]() ,
откуда
,
откуда![]() или
или
![]() (1.45)
(1.45)
где
электрический момент диполя
![]() .
.

Рис. 1.16. Диполь в однородном поле
Момент
сил (1.45) стремится повернуть диполь так,
чтобы его электрический момент
![]() установился
в направлении электрического поля
установился
в направлении электрического поля![]() .
.
Найдем потенциальную энергию, которой обладает диполь во внешнем электрическом поле (см. рис. 1.17):
![]() (1.46)
(1.46)
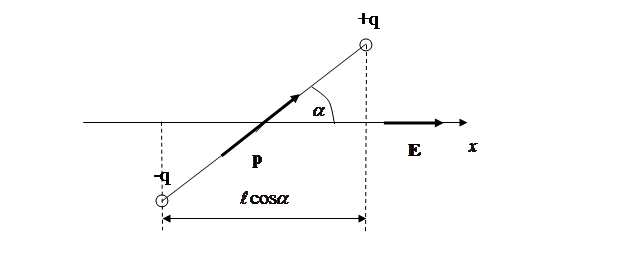
Рис. 1.17. К расчету потенциальной энергии диполя во внешнем поле
Потенциал
однородного поля убывает линейно в
направлении вектора
![]() .
Поэтому
.
Поэтому
 (1.47)
(1.47)
Подставим (1.47) в (1.46), найдем
![]() (1.48)
(1.48)
или в векторных обозначениях
![]() (1.49)
(1.49)
Формулы
(1.45) и (1.49) остаются справедливыми и в
неоднородном электрическом поле, так
как размером диполя
![]() пренебрегается
по сравнению с характерным размером
неоднородности поля.
пренебрегается
по сравнению с характерным размером
неоднородности поля.
В неоднородном внешнем электрическом поле на диполь действует сила
![]() (1.50)
(1.50)
Формула
(1.50) показывает, что в неоднородном
поле на диполь действует сила, направленная
в сторону наиболее быстрого уменьшения
потенциальной энергии диполя в этом
поле. Сила![]() приводит
диполь в поступательное движение.
Проиллюстрируем данный вывод на
конкретных примерах (см. рис. 1.18).
приводит
диполь в поступательное движение.
Проиллюстрируем данный вывод на
конкретных примерах (см. рис. 1.18).

Рис. 1.18. Поведение диполя в неоднородном поле
В
случае рис. 1.18, а диполь втягивается в
область более сильного поля, так как
![]() ,
и сила
,
и сила![]() ,
действующая на диполь, направлена слева
направо. Аналогично можно показать, что
диполь, ориентированный против поля,
выталкивается из поля. В случае рис.
1.18, б сила
,
действующая на диполь, направлена слева
направо. Аналогично можно показать, что
диполь, ориентированный против поля,
выталкивается из поля. В случае рис.
1.18, б сила![]() ,
действующая на диполь, направлена вверх
(в направлении ослабления поля) – диполь
смещается вверх, параллельно самому
себе.
,
действующая на диполь, направлена вверх
(в направлении ослабления поля) – диполь
смещается вверх, параллельно самому
себе.
|
|
|
Диэлектриками называют тела, не проводящие электрического тока.
Термин «диэлектрик» введен М. Фарадеем для обозначения веществ, через которые проникают электрические поля, в отличие от металлов, внутри которых электростатического поля нет. К диэлектрикам относят твердые тела, такие, как эбонит, фарфор, а также жидкости (например, чистая вода) и газы.
При изменении внешних условий (нагревание, воздействие ионизирующих излучений и т. п.) диэлектрик может проводить электрический ток. Изменение состояния диэлектрика при помещении в электрическое поле можно объяснить его молекулярным строением. Условно выделим три класса диэлектриков: 1) полярные; 2) неполярные; 3) кристаллические.
К первому классу принадлежат такие вещества, как вода, нитробензол и др. Молекулы этих диэлектриков не симметричны, «центры масс» их положительных и отрицательных зарядов не совпадают, поэтому такие молекулы обладают электрическим дипольным моментом даже в случае, когда электрического поля нет.
На рис. 12.19 схематически показаны молекулы соляной кислоты (а) и воды (б) и соответствующие им дипольные моменты в дебаях1. (1 Дебай (Д) — внесистемная единица дипольного момента молекул: 1Д = 3,33564 • 10-30Кл • м.)

В
отсутствие электрического поля дипольные
моменты молекул ориентированы хаотически
(рис. 12.20, а) и векторная сумма моментов
всех N
молекул
равна нулю:
![]()
Если
диэлектрик поместить в электрическое
поле, то дипольные моменты молекул
стремятся ориентироваться вдоль поля
(рис. 12.20, б),
однако
полной ориентации не будет вследствие
молекулярно-теплового хаотического
движения. В этом случае
![]()
Ко
второму классу диэлектриков относят
такие вещества (например, водород,
кислород и др.), молекулы которых в
отсутствие электрического поля не имеют
дипольных моментов. В таких молекулах
заряды электронов и ядер расположены
так, что «центры масс» положительных и
отрицательных зарядов совпадают. Если
неполярную молекулу поместить в
электрическое поле, то разноименные
заряды несколько сместятся в противоположные
стороны и молекула будет иметь дипольный
момент. На рис. 12.21 схематически в
виде кружков показаны молекулы такого
диэлектрика в отсутствие поля
![]() (а)
и при наложении поля
(а)
и при наложении поля
![]() (б)(стрелки
у кружков означают дипольные моменты
молекул).
(б)(стрелки
у кружков означают дипольные моменты
молекул).
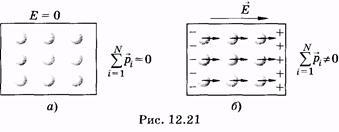
Третий класс — кристаллические диэлектрики (например, NaCl), решетка которых состоит из положительных и отрицательных ионов. Такой диэлектрик можно схематически рассматривать как совокупность двух «подрешеток», одна из которых заряжена положительно, другая — отрицательно. При отсутствии поля подрешетки расположены симметрично и суммарный электрический момент такого диэлектрика равен нулю1. (1 Строго говоря, ионные кристаллы могут обладать электрическим моментом и при отсутствии внешнего поля, однако здесь это не учтено.) Если диэлектрик поместить в электрическое поле, то подрешетки немного сместятся в противоположные стороны и диэлектрик приобретет электрический момент.
Все эти процессы, происходящие в разных диэлектриках при наложении электрического поля, объединяют общим термином поляризация, т. е. приобретение диэлектриком дипольного момента.
Для первого класса диэлектриков характерна ориентационная поляризация, для второго — электронная, т. е. смещение главным образом электронных оболочек, для третьего — ионная. Такая классификация условна, так как в реальном диэлектрике могут одновременно существовать все виды поляризации.
Изменение
напряженности электрического поля, в
котором находится диэлектрик, будет
влиять на состояние его поляризации.
Охарактеризовать степень поляризации
диэлектрика суммарным электрическим
моментом всех его N
молекул
![]() нельзя,
так как эта величина зависит, в частности,
от объема диэлектрика. Для оценки
состояния поляризации диэлектрика
вводят величину, называемуюполяризованностъю,
среднее
значение которой равно отношению
суммарного электрического момента
элемента объема V
диэлектрика
к этому объему:
нельзя,
так как эта величина зависит, в частности,
от объема диэлектрика. Для оценки
состояния поляризации диэлектрика
вводят величину, называемуюполяризованностъю,
среднее
значение которой равно отношению
суммарного электрического момента
элемента объема V
диэлектрика
к этому объему:
![]() (12.36)
(12.36)
Единицей поляризованности является кулон на квадратный метр (Кл/м2).
При поляризации диэлектрика на одной его поверхности (грани) создаются положительные заряды, а на другой — отрицательные (см. рис. 12.20, б и 12.21, б). Эти электрические заряды называют связанными, так как они принадлежат молекулам диэлектрика (или кристаллической решетке при ионной поляризации) и не могут перемещаться в отрыве от молекул или быть удалены с поверхности диэлектрика в отличие от свободных зарядов, которых в идеальном диэлектрике нет.
При возрастании напряженности электрического поля растет степень упорядоченности ориентации молекул (ориентационная поляризация), увеличиваются дипольные моменты молекул (электронная поляризация), а также происходит большее смещение «подрешеток» (ионная поляризация) — все это приводит к увеличению поверхностной плотности sсв связанных электрических зарядов.
Таким образом, sсв также характеризует степень поляризации диэлектрика.
Установим связь между Ре и sсв на примере поляризованного диэлектрика, имеющего форму параллелепипеда (рис. 12.22, а). Такой параллелепипед представим как совокупность диполей, которые, простоты ради, можно рассматривать как «цепочки»; одна из них показана на рис. 12.22, б. Так как внутренние части «цепочки» диполей электрически компенсируются, то такая «цепочка» подобна длинному диполю с расстоянием между зарядами, равным ребру параллелепипеда.
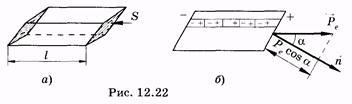
Если
на грани параллелепипеда с площадью S
возник связанный заряд </ов,
то суммарный электрический момент![]() всего
параллелепипеда численно равен дсв
/, но так как
всего
параллелепипеда численно равен дсв
/, но так как
![]() Объем
параллелепипедаV
= SI cos
a. На основании двух последних равенств
имеем
Объем
параллелепипедаV
= SI cos
a. На основании двух последних равенств
имеем
![]() (12.37)
(12.37)
Учитывая (12.36) и (12.37), получаем
![]()
откуда
![]()
Итак, поверхностная плотность связанных зарядов sсв равна нормальной к грани составляющей вектора Ре.
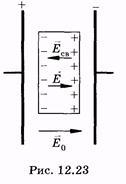 Рассмотрим,
например, плоский диэлектрик, расположенный
в однородном электрическом поле (рис.
12.23);
Рассмотрим,
например, плоский диэлектрик, расположенный
в однородном электрическом поле (рис.
12.23);
![]() —
напряженность поля в отсутствие
диэлектрика (поле в вакууме). Связанные
заряды создают однородное поле
напряженностью
—
напряженность поля в отсутствие
диэлектрика (поле в вакууме). Связанные
заряды создают однородное поле
напряженностью![]() ,
в
результате в диэлектрике будет
электрическое поле напряженностью
,
в
результате в диэлектрике будет
электрическое поле напряженностью
Е = Е0- Есв(12.39)
Известно, что диэлектрическая проницаемость среды e равна отношению силы взаимодействия зарядов в вакууме к силе взаимодействия этих же зарядов на том же расстоянии в среде:
F0/F = e, или F0 = eF.
Так как напряженность электрического поля пропорциональна силе, действующей на заряд [см. (12.1)], то аналогичное соотношение можно записать для Е0 и Е:
Е0 = eЕ. (12.40)
Напряженность электрического поля, образованного связанными электрическими зарядами, Есв = sсв/e0. Для данного примера из (12.38) имеем sсв = Ре, тогда Есв = Ре/e0. Подставляя эту формулу и (12.40) в (12.39), получаем Е = eЕ - Ре/e0, или Е(e0 - 1) = = Ре/e0, откуда
Ре = e0(e- 1)Е. (12.41)
Как и можно было ожидать, поляризованность пропорциональна напряженности электрического поля в диэлектрике. На основании (12.41) вводят понятие диэлектрической восприимчивости среды
c = e-1, (12-42)
которая вместе с диэлектрической проницаемостью e характеризует способность диэлектрика к поляризации и зависит от его молекулярного строения, а возможно и от температуры. В переменных электрических полях eиc изменяются также в зависимости от частоты.
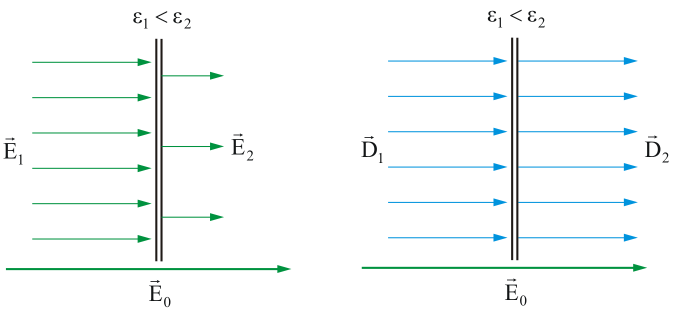
Имеем
границу раздела двух сред с
![]() и
и![]() ,
так что,
,
так что,
![]() (рис.
4.10, а).
(рис.
4.10, а).
а б
Рис. 4.10
Как мы уже показали, в соответствии с (4.1.10),
![]() или
или
![]() ,
,
т.е., напряженность электростатического поля E изменяется скачком при переходе из одной среды в другую.
Главная
задача электростатики – расчет
электрических полей, то есть
![]() в
различных электрических аппаратах,
кабелях, конденсаторах, и т.д. Эти расчеты
сами по себе не просты, да еще наличие
разного сорта диэлектриков и проводников
еще более усложняют задачу.
в
различных электрических аппаратах,
кабелях, конденсаторах, и т.д. Эти расчеты
сами по себе не просты, да еще наличие
разного сорта диэлектриков и проводников
еще более усложняют задачу.
Для упрощения расчетов была введена новая векторная величина – вектор электрического смещения (электрическая индукция):
|
|
|
(4.3.1) |
|
Из
предыдущих рассуждений
![]() ,
тогда
,
тогда![]() ,
отсюда
,
отсюда
|
|
|
(4.3.2) |
|
Таким
образом, вектор
![]() остается
неизменным при переходе из одной среды
в другую (рис. 4.10, б), и это облегчает
расчет
остается
неизменным при переходе из одной среды
в другую (рис. 4.10, б), и это облегчает
расчет![]() .
Зная
.
Зная![]() и
ε,
легко рассчитывать
и
ε,
легко рассчитывать
![]()
![]() ,
отсюда можно записать:
,
отсюда можно записать:
|
|
|
(4.3.3) |
|
где
![]() –
вектор поляризации, χ – диэлектрическая
восприимчивость среды, характеризующая
поляризацию единичного объема среды.
–
вектор поляризации, χ – диэлектрическая
восприимчивость среды, характеризующая
поляризацию единичного объема среды.
Таким
образом, вектор
![]() –
есть сумма (линейная комбинация) двух
векторов различной природы:
–
есть сумма (линейная комбинация) двух
векторов различной природы:![]() –
главной характеристики поля и
–
главной характеристики поля и![]() –
поляризации среды.
–
поляризации среды.
В
СГС:
![]() поэтому
в вакууме
поэтому
в вакууме![]() и
размерность у
и
размерность у![]() и
и![]() одинакова.
одинакова.
В
СИ:
![]() ,
т. е. это заряд, протекающий через единицу
поверхности.
,
т. е. это заряд, протекающий через единицу
поверхности.
Для
точечного заряда в вакууме
![]()
Для
![]() имеет
место принцип суперпозиции, как и для
имеет
место принцип суперпозиции, как и для![]() ,
т.е.
,
т.е.
![]()
Поток вектора
![]() через
произвольную замкнутую поверхность S
равен
через
произвольную замкнутую поверхность S
равен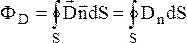 ,
где Dn- проекция вектора
,
где Dn- проекция вектора![]() на
нормаль
на
нормаль![]() к
площадке dS. Теорема Гаусса для
электростатического поля в диэлектрике
выводится аналогично выводу теоремы
для вакуума, в результате получаем
к
площадке dS. Теорема Гаусса для
электростатического поля в диэлектрике
выводится аналогично выводу теоремы
для вакуума, в результате получаем ,
где в правой части сумма свободных
зарядов.
,
где в правой части сумма свободных
зарядов.
Расчет напряженности и разности потенциалов некоторых электростатических полей
Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Остроградского–Гаусса.
|
|
Пример 1. Поле точечного заряда. Имеется
точечный электрический заряд
В любой
точке сферической поверхности
Используя это условие, вычислим полный поток через сферическую поверхность |
 .
(2.8)
.
(2.8)
С учетом (2.8) теорема Остроградского–Гаусса запишется в виде
![]() ,
,
откуда
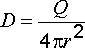 .
(2.9)
.
(2.9)
Используя формулу (2.2), определим напряженность электрического поля в среде по формуле
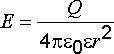 .
(2.10)
.
(2.10)
Используя связь напряженности электрического поля с потенциалом (гл. 1, § 2), определим распределение потенциала поля точечного заряда в пространстве.
Так как
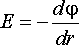 ,
то с учетом (2.10) получаем выражение
,
то с учетом (2.10) получаем выражение
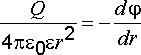 .
(2.11)
.
(2.11)
Интегрируя выражение (2.11) при переходе из бесконечности в данную точку А, получаем

или
при
![]()
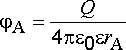 .
(2.12)
.
(2.12)
Пример 2. Электрическое поле равномерно заряженной сферической поверхности.
Рассмотрим электрическое поле,
создаваемое заряженной сферической
поверхностью (рис. 2.5). Пусть заряд
равномерно распределен по поверхности
сферы с поверхностной плотностью
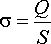 .
Из условия задачи очевидно, что линии
электрического смещения могут быть
только перпендикулярны заряженной
поверхности и расходиться радиально
от центра. Поэтому в качестве замкнутой
поверхности удобно выбрать сферу с
радиусом
.
Из условия задачи очевидно, что линии
электрического смещения могут быть
только перпендикулярны заряженной
поверхности и расходиться радиально
от центра. Поэтому в качестве замкнутой
поверхности удобно выбрать сферу с
радиусом![]() .
.
Исследуем электрическое поле в точках А, В и С (рис. 2.5):
|
|
а) рассмотрим точки электрического
поля внутри шара. Выберем произвольную
точку А и проведем через нее сферическую
поверхность с радиусом
Равенство (2.13) выполняется при условии, что
Следовательно, в любой точке, расположенной внутри заряженной сферической поверхности, вектор электрического смещения равен нулю. |
Используя условия:
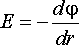 и
и![]() ,
из формулы (2.14) следует
,
из формулы (2.14) следует
![]() .
(2.15)
.
(2.15)
Формула (2.15) указывает, что все точки внутри сферы имеют одинаковые потенциалы;
б) рассмотрим точки поля на поверхности
сферы. Выберем сферическую поверхность
с радиусом
![]() и
запишем теорему Остроградского–Гаусса
и
запишем теорему Остроградского–Гаусса
![]() ,
,
где
![]() –
заряд, распределенный по поверхности
сферы.
–
заряд, распределенный по поверхности
сферы.
Из условия симметрии задачи очевидно,
что
![]() для
всех точек сферической поверхности.
Интегрирование по замкнутой поверхности
радиусом
для
всех точек сферической поверхности.
Интегрирование по замкнутой поверхности
радиусом![]() дает
дает
![]() .
.
Так как
![]() ,
то имеем
,
то имеем![]() или
или
 ;
(2.16)
;
(2.16)
в) рассмотрим точки поля за пределами
сферической поверхности. Выберем
произвольную точку С и проведем
через нее сферическую поверхность с
радиусом
![]() .
Для выбранной поверхности запишем
теорему Остроградского–Гаусса
.
Для выбранной поверхности запишем
теорему Остроградского–Гаусса
![]() ,
,
где
![]() ;
;![]() –
заряд на поверхности сферы.
–
заряд на поверхности сферы.
Из условия симметрии задачи опять
очевидно, что
![]() для
всех точек выбранной поверхности. После
интегрирования по замкнутой поверхности
радиусом
для
всех точек выбранной поверхности. После
интегрирования по замкнутой поверхности
радиусом![]() получаем
получаем
![]() .
.
После упрощения имеем
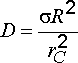 или
или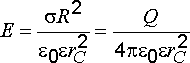 .
(2.17)
.
(2.17)
Используя формулу (2.17) и условия
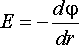 и
и![]() ,
получаем
,
получаем
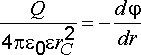 ,
откуда
,
откуда .
.
Проинтегрируем полученное выражение
 ,
,
принимая
![]() ,
получаем
,
получаем
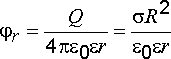 .
(2.18)
.
(2.18)
Потенциал поверхности сферы определим
из (2.18), используя условие
![]() ,
,
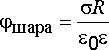 .
(2.19)
.
(2.19)
Графики зависимости
![]() и
j от расстояния до центра заряженной
сферической поверхности представлены
на рис. 2.6 и 2.7.
и
j от расстояния до центра заряженной
сферической поверхности представлены
на рис. 2.6 и 2.7.
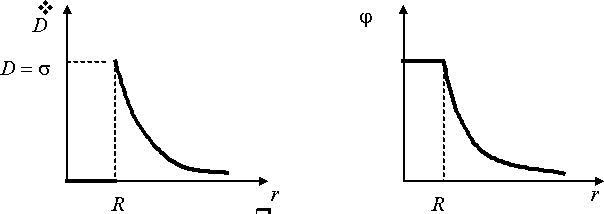
Рис. 2.6. Зависимость
![]() электрического
Рис. 2.7. Зависимость
электрического
Рис. 2.7. Зависимость![]() электрического
поля
электрического
поля
поля заряженной сферы заряженной сферы
Пример 3. Электрическое поле равномерно заряженной плоскости
Имеется безграничная плоскость,
заряженная равномерно с поверхностной
плотностью
![]() .
Из симметрии задачи очевидно, что линии
смещения могут быть направлены только
перпендикулярно плоскости и равномерно
распределены по поверхности. При записи
теоремы Остроградского–Гаусса в
качестве замкнутой поверхности удобно
выбрать прямой цилиндр, перпендикулярный
заряженной плоскости, ограниченный
двумя плоскими основаниями площадью
.
Из симметрии задачи очевидно, что линии
смещения могут быть направлены только
перпендикулярно плоскости и равномерно
распределены по поверхности. При записи
теоремы Остроградского–Гаусса в
качестве замкнутой поверхности удобно
выбрать прямой цилиндр, перпендикулярный
заряженной плоскости, ограниченный
двумя плоскими основаниями площадью![]() ,
расположенными по обеим сторонам
заряженной плоскости (рис. 2.8).
,
расположенными по обеим сторонам
заряженной плоскости (рис. 2.8).
Полный поток электрического смещения через выбранную замкнутую поверхность
![]() .
.
|
|
Так как образующие цилиндра параллельны
линиям смещения ( Применяя теорему Остроградского–Гаусса, имеем
откуда
|
Напряженность поля равномерно заряженной плоскости
 .
(2.21)
.
(2.21)
Из (2.21) вытекает, что безграничная заряженная плоскость создает однородное электрическое поле.
Потенциалы поля изменяются только в направлении, перпендикулярном плоскости, и разность потенциалов между точками в этом направлении определится как
 .
(2.22)
.
(2.22)
Пример 4. Поле равномерно заряженного
цилиндра (нити).Рассмотрим безграничный
цилиндр (нить), равномерно заряженный
по длине с линейной плотностью заряда![]() ,
гдеd – длина
цилиндра.
,
гдеd – длина
цилиндра.
Из условия симметрии линии смещения будут радиальными прямыми, перпендикулярными к поверхности цилиндра. В этом случае в качестве поверхности для вычисления потока удобно выбрать цилиндрическую поверхность Sпоказанную на рис. 2.9.
Так как поток через основание выбранного
цилиндра равен нулю (![]() ),
а боковая поверхность перпендикулярна
к линиям смещения (
),
а боковая поверхность перпендикулярна
к линиям смещения (![]() ),
то полный поток через замкнутую
поверхность
),
то полный поток через замкнутую
поверхность
![]() .
.
|
|
Применяя теорему Остроградского–Гаусса, имеем
Отсюда получаем, что электрическое
смещение поля в точках, отстоящих на
расстоянии
С учетом выражения (2.2) напряженность электрического поля, созданного заряженным цилиндром (нитью), составит
|
Так как
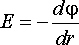 ,
то с учетом (2.24) разность потенциалов
между точками, удаленными от оси цилиндра
на расстояние
,
то с учетом (2.24) разность потенциалов
между точками, удаленными от оси цилиндра
на расстояние![]() ,
определится по формуле
,
определится по формуле
 (2.25)
(2.25)
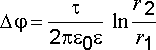 .
.
Выражения (2.24) и (2.25) показывают, что электрическое поле, создаваемое заряженным цилиндром (нитью), имеет цилиндрическую симметрию.
Пример 5. Электрическое поле диполя.
|
|
Система жестко связанных разноименных точечных зарядов называется электрическим диполем (рис. 2.10).
Произведение заряда
|
Вектор дипольного момента направлен вдоль оси диполя от отрицательного заряда к положительному.
Согласно принципу суперпозиции потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, вызываемых отдельными зарядами
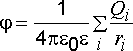 ,
(2.26)
,
(2.26)
где
j – потенциал результирующего поля в
рассматриваемой точке относительно
бесконечности;
![]() –
расстояние этой точки до
–
расстояние этой точки до![]() -го
заряда.
-го
заряда.
Согласно (2.26) потенциал электрического поля, созданный электрическим диполем в некоторой точке А (рис. 2.11), определится как
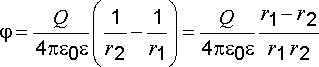 .
.
|
|
Будем считать, что длина диполя
Тогда выражение для потенциала принимает вид
Используя
связь потенциала с напряженностью,
можно определить напряженность
электрического поля. Для расчета
напряженности электрического поля
воспользуемся полярными координатами
Тогда составляющая
напряженности в направлении радиуса
|
 .
(2.28)
.
(2.28)
Составляющая,
перпендикулярная радиусу-вектору
![]() ,
,
 .
(2.29)
.
(2.29)
Полная величина напряженности электрического поля в точке А определится по формуле
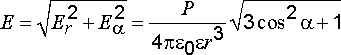 ,
(2.30)
,
(2.30)
 ,
(2.31)
,
(2.31)
где β – угол, образованный вектором
напряженности электрического поля и
радиусом-вектором
![]() .
.
|
|
Электроемкость уединенного проводника.
Рассмотрим проводник, удаленный от других проводников, тел и зарядов в связи с чем его можно рассматривать как уединенный проводник. Из опыта следует, что между зарядом и потенциалом существует зависимость q = Сj.
Величину
![]() (3.5.2)
(3.5.2)
называют
электроемкостью или просто емкостью
уединенного проводника. Эта величина
численно равна заряду, сообщение которого
проводнику повышает его потенциал на
единицу. Емкость зависит от формы и
размеров проводника и не зависит от
материала, агрегатного состояния и от
размеров полостей внутри проводника.
Емкость также не зависит от заряда и
потенциала проводника. Последнее
утверждение не противоречит формуле
(3.5.2). ее следует читать так, что потенциал
проводника пропорционален его заряду
и обратно пропорционален емкости.
Попробуем найти емкость уединенного
проводника, имеющего форму шара радиусом
R. Для этого определим потенциал шара,
использовав формулу, связывающую
![]() и
j:
и
j:
![]() .
(3.5.3)
.
(3.5.3)
Если полученный результат подставить в формулу (3.5.2) то для С получим:
![]() .
(3.5.4)
.
(3.5.4)
За единицу емкости в системе СИ принимают емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл. Эта единица называется фарадом (Ф). Фарад - очень большая единица. Если землю рассматривать как проводящий шар радиусом 6400 км, то емкость ее равняется примерно 700×10-6Ф. Поэтому на практике чаще приходится встречаться с емкостями мкФ = 10-6Ф и nФ = 10-12Ф.
Взаимная емкость . Конденсаторы.
Если к уединенному проводнику приближать другие проводники, то емкость первого проводника будет увеличиваться. Это связано с тем, что на приближающихся проводниках поле данного проводника будет вызывать перераспределение зарядов. Например, положительно заряженный проводник на приближающемся проводнике вызывает такое перераспределение, что индуцированные отрицательные заряды оказываются ближе к проводнику чем положительные. Поэтому потенциал проводника, который определяется суммой потенциала собственных зарядов и зарядов, индуцированных на других телах, уменьшится. Следовательно, его емкость по (3.5.2) увеличится таким образом можно создать систему проводников, которая будет обладать емкостью, значительно большей, чем емкость уединенного проводника. Наибольший практический интерес представляет система проводников, близко расположенных друг-другу и заряженных одинаковыми по величине, но противоположными по знаку зарядами. Такую систему называют конденсатором, а проводники – его обкладками. Емкость конденсатора определяется:
![]() ,
(3.5.5)
,
(3.5.5)
где j1 - j2 –разность потенциалов между обкладками, q – заряд, расположенный на положительно заряженной обкладке конденсатора. Разность потенциалов иногда называют напряжением и обозначают буквой U. Поэтому формулу (3.5.5) можно записать:
![]() .
(3.5.6)
.
(3.5.6)
По форме обкладок конденсаторы бывают плоские, цилиндрические и сферические. Определим емкость плоского конденсатора. Пусть площадь обкладки S а заряд на ней q. Напряженность поля между обкладками, как мы ранее определили
![]() .
(3.5.7)
.
(3.5.7)
Исходя из формулы (3.4.16 ) разность потенциалов между обкладками
![]() ,
(3.5.8)
,
(3.5.8)
отсюда для емкости конденсатора получаем:
![]() ,
(3.5.9)
,
(3.5.9)
где d – расcтояние между обкладками; e - диэлектрическая проницаемость среды, заполняющий зазор между обкладками. Нетрудно получить для емкости цилиндрического конденсатора формулу:
![]() ,
(3.5.10)
,
(3.5.10)
где
![]() -
длина конденсатора, R1
и R2
– радиусы внутренней и наружной
цилиндрических обкладок. Емкость
сферического конденсатора определяется
формулой:
-
длина конденсатора, R1
и R2
– радиусы внутренней и наружной
цилиндрических обкладок. Емкость
сферического конденсатора определяется
формулой:
![]() ,
(3.5.11)
,
(3.5.11)
где R1 и R2 – радиусы внутренней и наружной обкладок. Отметим, что формулы (3.5.10) и (3.5.11) при малом зазоре между обкладками переходят в формулу (3.5.9)
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0 с одной
обкладки на другую (рис. 1.7.1). При этом
одна обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на обкладках
уже имеется некоторый заряд q, а между
ними существует некоторая разность
потенциалов
![]() при
переносе каждой порции Δq внешние силы
должны совершить работу
при
переносе каждой порции Δq внешние силы
должны совершить работу
Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
|
|
|
|
|
|
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.
|
Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)
|
|
где k – жесткость пружины, x – деформация, F = kx – внешняя сила.
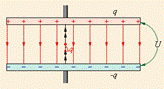
По
современным представлениям, электрическая
энергия конденсатора локализована в
пространстве между обкладками
конденсатора, то есть в электрическом
поле. Поэтому ее называют энергией
электрического поля. Это легко
проиллюстрировать на примере заряженного
плоского конденсатора. Напряженность
однородного поля в плоском конденсаторе
равна E = U/d, а его емкость
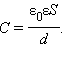 Поэтому
Поэтому
|
|
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
|
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладаетпотенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.
Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближаяq2кq1либоq1кq2. В обоих случаях совершается одинаковая работа:

В
последней формуле
![]() -
потенциал поля 1-го заряда в том месте,
где находится второй заряд;
-
потенциал поля 1-го заряда в том месте,
где находится второй заряд;![]() -
потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
-
потенциал поля второго заряда в том
месте, где находится первый заряд. С
учетом сказанного, эту формулу можно
записать также в виде:
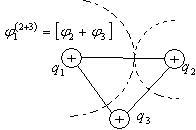
![]() .
.
Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:
![]()
В
общем случае системы n неподвижных
точечных зарядовэнергия системыопределяется по формуле:![]() .
.
Если
проводник поместить во внешнее
электростатическое поле или зарядить
его, то на заряды данного проводника
будет действовать электростатическое
поле, под действием которого они начнут
двигаться. Движение зарядов (ток) будет
длиться до тех пор, пока не установится
равновесное распределение зарядов, при
котором электростатическое поле внутри
данного проводника обращается в нуль.
Это происходит в течение очень короткого
времени. Действительно, если бы поле не
было равно нулю, то в проводнике появилось
бы упорядоченное движение зарядов без
затраты энергии от внешнего источника,
что не согласуется с законом сохранения
энергии. Значит, напряженность поля во
всех точках внутри проводника равна
нулю:
![]() Если
внутри проводника электрического поле
отсутствует, то потенциал во всех точках
внутри проводника одинаков (φ = const), т.
е.поверхность проводника в
электростатическом поле является
эквипотенциальной. Это означает, что
вектор напряженности поля на внешней
поверхности проводника направлен по
перпендикуляру к каждой точке его
поверхности. Если это было бы не так, то
под действием касательной
составляющейЕзаряды начали
бы перемещаться по поверхности проводника,
что, в свою очередь, противоречило бы
равновесному распределению зарядов.
Если
проводнику дать некоторый дополнительный
заряд Q, то нескомпенсированные заряды
разместятьсятолько на поверхности
проводника. Это вытекает непосредственно
из теоремы Гаусса, согласно которой
заряд Q, который находится внутри
проводника в некотором объеме, ограниченном
произвольной замкнутой поверхностью,
равен
Если
внутри проводника электрического поле
отсутствует, то потенциал во всех точках
внутри проводника одинаков (φ = const), т.
е.поверхность проводника в
электростатическом поле является
эквипотенциальной. Это означает, что
вектор напряженности поля на внешней
поверхности проводника направлен по
перпендикуляру к каждой точке его
поверхности. Если это было бы не так, то
под действием касательной
составляющейЕзаряды начали
бы перемещаться по поверхности проводника,
что, в свою очередь, противоречило бы
равновесному распределению зарядов.
Если
проводнику дать некоторый дополнительный
заряд Q, то нескомпенсированные заряды
разместятьсятолько на поверхности
проводника. Это вытекает непосредственно
из теоремы Гаусса, согласно которой
заряд Q, который находится внутри
проводника в некотором объеме, ограниченном
произвольной замкнутой поверхностью,
равен![]() поскольку
во всех точках внутри замкнутой
поверхности D=0.
Теперь мы будем
искать взаимосвязь между напряженностью
Е поля вблизи поверхности заряженного
проводника и поверхностной плотностью
зарядов на его поверхности σ . Для этого
используем теорему Гаусса для бесконечно
малого цилиндра с основаниями ΔS, который
пересекает границу проводник—диэлектрик.
Ось цилиндра направлена вдоль
вектораЕ(рис. 1). Поток вектора
электрического смещения через внутреннюю
часть цилиндрической поверхности равен
нулю, так как внутри проводникаЕ1(а
следовательно, иD1) есть
нуль, поэтому поток вектораDсквозь
замкнутую цилиндрическую поверхность
определяется только потоком сквозь
наружное основание цилиндра. Используя
теорему Гаусса, этот поток (DΔS) равен
сумме зарядов (Q=σΔS), находящихся внутри
поверхности: DΔS=σΔS т.е.
поскольку
во всех точках внутри замкнутой
поверхности D=0.
Теперь мы будем
искать взаимосвязь между напряженностью
Е поля вблизи поверхности заряженного
проводника и поверхностной плотностью
зарядов на его поверхности σ . Для этого
используем теорему Гаусса для бесконечно
малого цилиндра с основаниями ΔS, который
пересекает границу проводник—диэлектрик.
Ось цилиндра направлена вдоль
вектораЕ(рис. 1). Поток вектора
электрического смещения через внутреннюю
часть цилиндрической поверхности равен
нулю, так как внутри проводникаЕ1(а
следовательно, иD1) есть
нуль, поэтому поток вектораDсквозь
замкнутую цилиндрическую поверхность
определяется только потоком сквозь
наружное основание цилиндра. Используя
теорему Гаусса, этот поток (DΔS) равен
сумме зарядов (Q=σΔS), находящихся внутри
поверхности: DΔS=σΔS т.е.![]() (1)
или
(1)
или![]() (2)
где
ε — диэлектрическая проницаемость
среды, находящаяся вокруг проводника.
Значит,
напряженность электростатического
поля у поверхности проводника задается
поверхностной плотностью зарядов. Можно
показать, что формула (2) задает
напряженность электростатического
поля вблизи поверхности проводника
абсолютно произвольной формы.
Если
во внешнее электростатическое поле
поместить нейтральный проводник, то
свободные заряды (электроны, ионы) будут
совершать движение: положительные —
по полю, отрицательные — против поля
(рис. 2, а). На одном конце проводника
будет собираться избыток положительного
заряда, на другом — избыток отрицательного
заряда. Эти заряды
называютсяиндуцированными(наведенными).
Процесс будет продолжаться до тех пор,
пока внутри проводника напряженность
поля не станет равной нулю, а линии
напряженности вне проводника —
перпендикулярными его поверхности
(рис. 2, б). Значит, нейтральный проводник,
который внесен в электростатическое
поле, разрывает часть линий напряженности;
эти линии напряженности заканчиваются
на отрицательных индуцированных зарядах
и вновь начинаются на положительных.
Индуцированные заряды распределяются
на внешней поверхности нашего проводника.
Явление перераспределения поверхностных
зарядов на проводнике во внешнем
электростатическом поле
называетсяэлектростатической
индукцией.
Из рис. 2, б мы видим,
что индуцированные заряды образуются
на проводнике вследствие смещения их
под действием поля, т. е. σ есть поверхностной
плотностью смещенных зарядов. Согласно
(1), электрическое смещение D вблизи
проводника численно равно поверхностной
плотности смещенных зарядов. По этой
причине векторDполучил
название вектора электрического
смещения.
(2)
где
ε — диэлектрическая проницаемость
среды, находящаяся вокруг проводника.
Значит,
напряженность электростатического
поля у поверхности проводника задается
поверхностной плотностью зарядов. Можно
показать, что формула (2) задает
напряженность электростатического
поля вблизи поверхности проводника
абсолютно произвольной формы.
Если
во внешнее электростатическое поле
поместить нейтральный проводник, то
свободные заряды (электроны, ионы) будут
совершать движение: положительные —
по полю, отрицательные — против поля
(рис. 2, а). На одном конце проводника
будет собираться избыток положительного
заряда, на другом — избыток отрицательного
заряда. Эти заряды
называютсяиндуцированными(наведенными).
Процесс будет продолжаться до тех пор,
пока внутри проводника напряженность
поля не станет равной нулю, а линии
напряженности вне проводника —
перпендикулярными его поверхности
(рис. 2, б). Значит, нейтральный проводник,
который внесен в электростатическое
поле, разрывает часть линий напряженности;
эти линии напряженности заканчиваются
на отрицательных индуцированных зарядах
и вновь начинаются на положительных.
Индуцированные заряды распределяются
на внешней поверхности нашего проводника.
Явление перераспределения поверхностных
зарядов на проводнике во внешнем
электростатическом поле
называетсяэлектростатической
индукцией.
Из рис. 2, б мы видим,
что индуцированные заряды образуются
на проводнике вследствие смещения их
под действием поля, т. е. σ есть поверхностной
плотностью смещенных зарядов. Согласно
(1), электрическое смещение D вблизи
проводника численно равно поверхностной
плотности смещенных зарядов. По этой
причине векторDполучил
название вектора электрического
смещения.
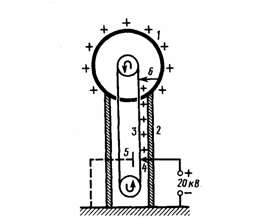
Поскольку в состоянии равновесия заряды отсутствуют внутри проводника, то создание внутри него полости не окажет влияния на конфигурацию расположения зарядов и тем самым на электростатическое поле. Значит, поле будет отсутствовать внутри полости. Если теперь заземлить данный проводник с полостью, то потенциал во всех точках полости будет равен нулю, т. е. полость полностью является изолированной от влияния внешних электростатических полей. На этом основана электростатическая защита— экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Для защиты вместо сплошного проводника может быть использована густая металлическая сетка, которая, также эффективна при наличии не только постоянных, но и переменных электрических полей. Свойство зарядов располагаться на внешней поверхности проводника на практике используется для устройстваэлектростатических генераторов, которые предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, который изобретен американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 3), укрепленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, которые соединены с одним из полюсов источника, второй полюс которого заземлен. Заземленная пластина 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Значит, сфера постепенно получает большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы широко применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.
Индуцированные заряды- это заряды противоположного знака, появившиеся в результате разделения у концов проводника.
Результирующие поле определяется как суперпозиция внешнего поля и поля
индуцированных зарядов. Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах проводящего тела появятся противоположные индуцированные заряды.
Экранировка электростатического поля: Если внесенное во внешнее электрическое поле тело не было заряжено, то сумма наведенных на нем зарядов оказывается равной нулю. Эти заряды распределяются так, чтобы их поле внутри проводящего тела в точности скомпенсировало внешнее поле. Ничто не изменится, если проводящее тело будет полым – во всей полости тела поле также будет отсутствовать. Этим обстоятельством широко пользуются дляэлектростатического экранированияразличных приборов и аппаратов от внешних электрических полей. С этой целью приборы помещают в замкнутые металлические оболочки, называемые экранами. Как показывает опыт, экраны можно выполнять и из мелкой металлической сетки.


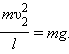

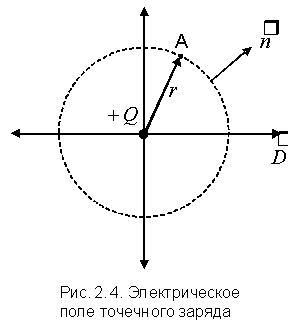
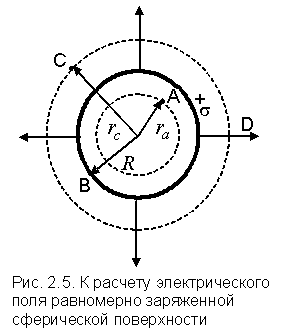

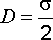 .
(2.20)
.
(2.20)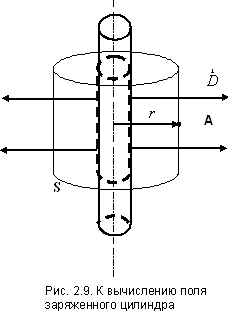
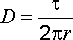 .
(2.23)
.
(2.23)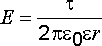 .
(2.24)
.
(2.24)
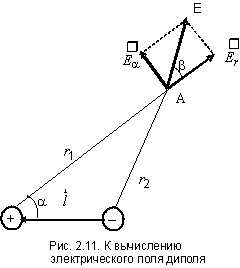
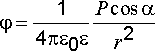 .
(2.27)
.
(2.27)