
- •Е.Г. Лаврушина, н.Л. Слугина Теория систем и системный анализ Практикум
- •Практикум по курсу Лабораторная работа №1 Решение логических задач
- •Краткие теоретические сведения
- •Контрольный пример Задача 1. «Пять офицеров»
- •Решение задачи:
- •Задача 2. «Финальный забег»
- •Решение задачи:
- •Индивидуальное задание
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Контрольные вопросы
- •Лабораторная работа № 2Классификация систем
- •Краткие теоретические сведения
- •Контрольный пример
- •Индивидуальное задание
- •Контрольные вопросы:
- •Лабораторная работа № 3 Принятие решений в условиях недостатка информации
- •Краткие теоретические сведения
- •Простые задачи Контрольный пример
- •Индивидуальное задание
- •Вариант1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Усложненные задачи Контрольный пример
- •Выводы:
- •Индивидуальное задание
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Контрольные вопросы
- •Лабораторная работа №4 Принятие решений в условиях неопределенности. Игры с природой
- •Краткие теоретические сведения
- •Контрольный пример
- •Решение
- •Критерий Вальда
- •Критерий минимаксного риска Сэвиджа
- •Критерий пессимизма-оптимизма Гурвица
- •Индивидуальное задание
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Контрольные вопросы
- •Лабораторная работа №5 Метод анализа иерархий
- •Краткие теоретические сведения
- •Этапы маи
- •Контрольный пример
- •3.1. Критерий «Внешность»
- •3.2. Критерий «Знание языка»
- •3.3. Критерий «Делопроизводство»
- •3.4. Критерий «Знание компьютера»
- •3.5. Критерий «Умение общаться по телефону»
- •4. Рассчитаем вектор глобальных приоритетов.
- •Индивидуальное задание
- •Контрольные вопросы:
- •Лабораторная работа № 6 Модели управления запасами
- •Краткие теоретические сведения
- •6.1. Общие определения
- •6.2. Краткая характеристика моделей управления запасами
- •Контрольный пример 1
- •Решение:
- •Контрольный пример 2
- •Решение
- •Индивидуальное задание
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Контрольный пример 1 Задача с. Джонсона для двух станков
- •Решение
- •Контрольный пример 2 Задача распределения заказов
- •Решение
- •Индивидуальное задание
- •Вариант 1
- •Вариант2
- •Вариант 3
- •Вариант4
- •Вариант 5
- •Вариант6
- •Вариант 7
- •Вариант8
- •Вариант 9
- •Вариант10
- •Контрольные вопросы
- •Лабораторная работа №8 Решение задач по оптимизации
- •Краткие теоретические сведения
- •8.1. Линейная оптимизационная задача Контрольный пример
- •Решение
- •Решение задачи с помощью ms Excel
- •Индивидуальное задание
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •8.2. Транспортная задача Контрольный пример
- •Решение задачи с помощью ms Excel.
- •Индивидуальное задание
- •Вариант 1
- •Вариант2
- •Вариант3
- •Вариант4
- •Вариант5
- •Вариант 6
- •Список рекомендуемой литературы
- •Оглавление
6.2. Краткая характеристика моделей управления запасами
1. Модель оптимального размера заказа
Предпосылки: 1)темп спроса на товар известен и постоянен; 2) получение заказа мгновенно; 3) отсутствуют количественные скидки при закупке больших партий товара; 4) единственные меняющиеся параметры - издержки заказа и хранения; 5) исключается дефицит в случае своевременного заказа.
Исходные данные: темп спроса, издержки заказа и хранения.
Результат: оптимальный размер заказа, время между заказами и их количество за период.
2. Модель оптимального размера заказа в предположении, что получение заказа не мгновенно
Следовательно, нужно найти объем запасов, при котором необходимо делать новый заказ.
Исходные данные: темп спроса, издержки заказа и хранения, время выполнения заказа.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса.
3. Модель оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль
Необходимо найти точку восстановления.
Исходные данные: темп спроса, издержки заказа и хранения, упущенная прибыль.
Результат: оптимальный размер заказа, время между заказами. точка восстановления запаса.
4. Модель с учетом производства (в сочетании с условиями 1-3)
Необходимо рассматривать уровень ежедневного производства и уровень ежедневного спроса.
Исходные данные: темп спроса, издержки заказа, хранения и упущенная прибыль, темп производства.
Результат: оптимальный уровень запасов (точка восстановления запаса).
5. Модель с количественными скидками
Появляется возможность количественных скидок в зависимости от размера заказа. Рассматривается зависимость издержек хранения от цены товара. Оптимальный уровень заказа определяется исходя из условия минимизации общих издержек для каждого вида скидок.
Модели типа 1-5 с вероятностным распределением спроса и времени выполнения заказа
Вместо предпосылки о постоянстве и детерминированности спроса на товар используется более реалистичный подход о предполагаемой известности распределения темпа спроса и времени выполнения заказа.
Рассмотрим подробнее модели с фиксированным размером заказа.
Модель 1. Наиболее экономичного размера заказа. Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен Q, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период (рис.6.1).
Пусть Q - размер заказа; Т - протяженность периода планирования; D - величина спроса за период планирования; d - величина спроса в единицу времени; К - издержки заказа; Н - удельные издержки хранения за период; h - удельные издержки хранения в единицу времени. Тогда:
(D/Q)K - совокупные издержки заказа;
(Q/2)H - совокупные издержки хранения;
d = D/T; h = H/T;
Q* =(2dK/h)1/2 (2DK/H)1/2 - оптимальный размер заказа;
N = D/Q* - оптимальное число заказов за период;
t* = Q*/d = T/N - время цикла (оптимальное время между заказами).
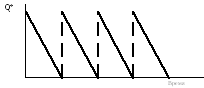
Рис. 6.1. Модель 1. Наиболее экономичного размера заказа
Модель 2. Введем предположение о том, что заказ может быть получен не мгновенно, а с течением времени. Тогда нам необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе. Следовательно, нам необходимо найти тот уровень запасов, при котором делается новый заказ. Этот уровень называется точкой восстановления R. Пусть L - время выполнения заказа. Тогда R = величина спроса в единицу времени, умноженная на время выполнения заказа = d L. Другие характеристики системы определяются так же, как и в модели 1. Модель иллюстрируется рис.6.2.

Рис. 6.2. Модель 2
