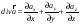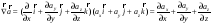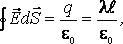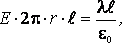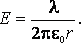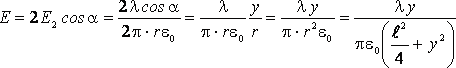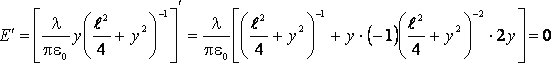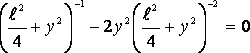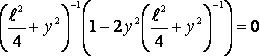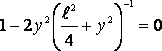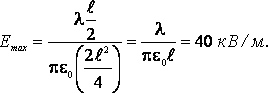Kol_Fizika_3_semmestr / Кол. Физика 3 семместр / 19 билет / bilet_19
.docxЗадача
Две
длинные параллельные нити равномерно
заряжены каждая с линейной плотностью ![]() =
0,50 мкКл/м. Расстояние между нитями
=
0,50 мкКл/м. Расстояние между нитями ![]() =
45 см. Найти максимальное значение модуля
напряженности электрического поля в
плоскости симметрии этой системы,
расположенной между нитями.
=
45 см. Найти максимальное значение модуля
напряженности электрического поля в
плоскости симметрии этой системы,
расположенной между нитями.
Решение.
|
|
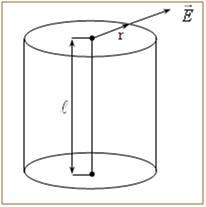
Найдем чему равен модуль напряженности поля бесконечной равномерно заряженной нити на расстоянии r от нее. Для этого воспользуемся теоремой Гаусса. Поскольку модуль вектора напряженности в каждой точке зависит только от расстояния r до нити, то в качестве воображаемой замкнутой поверхности выбираем цилиндр: |
|
|
|
|
|
|
|
|
|
|
|
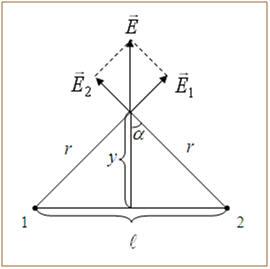
Воспользуемся принципом суперпозиции, как видно из рисунка
|
|
|
|
Чтобы найти максимальное значение модуля напряженности электрического поля, продифференцируем полученное выражение и приравняем его к нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теория 2
4.6. Энергия заряженного проводника.
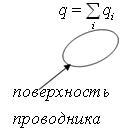
Заряд, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов q:
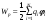
Поверхность
проводника является эквипотенциальной.
Потенциалы
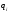 одинаковы и равны
одинаковы и равны
 .
.
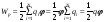
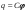 ;
;
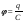 ;
;
4.1. Энергия взаимодействия системы зарядов.
Ранее
мы получили формулу для потенциальной
энергии взаимодействия зарядов
 и
и
 :
:
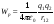
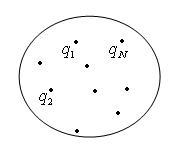
Пусть
имеется система состоящая из N
точечных зарядов
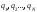 .
.
Тогда потенциальная энергия взаимодействия будет равна:
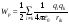
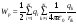
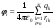
-
потенциал, создаваемый всеми зарядами
кроме
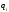 в точке, где помещается заряд
в точке, где помещается заряд
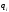 .
.
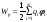
4.2. Полная энергия взаимодействия.
Выше мы получили для энергии взаимодействия зарядов:
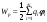 (4.1)
(4.1)
Если
заряды распределены непрерывно, то,
разлагая систему зарядов на совокупность
электрических зарядов
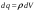 и переходя от суммирования к интегрированию,
получим:
и переходя от суммирования к интегрированию,
получим:
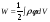 (4.2)
(4.2)
В (4.1) и (4.2) потенциал имеет различный смысл. С одной стороны по (4.1):
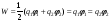
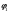 - потенциал, созданный в месте, где
находится заряд
- потенциал, созданный в месте, где
находится заряд
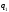 ,
зарядом
,
зарядом
 .
.
Согласно
(4.2), мы должны разбить заряд каждого
шарика на бесконечно малые элементы
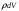 и каждый из них умножить на потенциал
и каждый из них умножить на потенциал
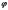 ,
создаваемый не положительными зарядами
другого шарика, и элементами заряда
этого шарика.
,
создаваемый не положительными зарядами
другого шарика, и элементами заряда
этого шарика.
![]()
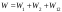 ,
,
где
 - энергия взаимодействия друг с другом
элементов 1 шара
- энергия взаимодействия друг с другом
элементов 1 шара
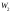 -
энергия взаимодействия друг с другом
элементов 2 шара
-
энергия взаимодействия друг с другом
элементов 2 шара
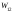 - энергия взаимодействия элементов 1
шара с элементами 2 шара
- энергия взаимодействия элементов 1
шара с элементами 2 шара
Теория 1
-
Дивергенция. Теорема Остроградского-Гаусса.
Интегральные теоремы
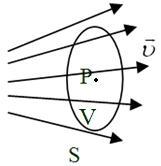
Пусть дано поле вектора
скорости несжимаемой неразрывной
жидкости. Возьмём в окрестности точки
P
воображаемую замкнутую поверхность S.
Если в объеме V,
ограниченном этой поверхностью, жидкость
не исчезает и не возникает, то поток,
вытекающий наружу, будет равен нулю.
Отличие потока жидкости
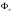 от нуля будет указывать на то, что
внутри жидкости имеются источники или
стоки, то есть точки, из которых жидкость
поступает в объём(источник), либо
удаляется из объёма(сток). Величина
потока определяет суммарную
алгебраическую мощность источников и
стоков.
от нуля будет указывать на то, что
внутри жидкости имеются источники или
стоки, то есть точки, из которых жидкость
поступает в объём(источник), либо
удаляется из объёма(сток). Величина
потока определяет суммарную
алгебраическую мощность источников и
стоков.
Мощность источника – объём жидкости. Выделяемый в единицу времени.
Отношение потока
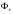 к
объёму V, из которого он
вытекает, даёт среднюю удельную
мощность источников, заключённых
в объёме V.
к
объёму V, из которого он
вытекает, даёт среднюю удельную
мощность источников, заключённых
в объёме V.
Пусть
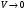 .
Объём стягивается к точке P.
Тогда
.
Объём стягивается к точке P.
Тогда
 -
удельная мощность источника в точке P,
которую называют дивергенцией или
расхождением вектора
-
удельная мощность источника в точке P,
которую называют дивергенцией или
расхождением вектора
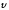 .
.

Для любого вектора
 :
:
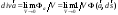
Зная дивергенцию вектора
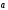 в любой точке пространства, можно
вычислить поток вектора через замкнутую
поверхность конечных размеров. Для
жидкости:
в любой точке пространства, можно
вычислить поток вектора через замкнутую
поверхность конечных размеров. Для
жидкости:
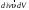 -
мощность источников, заключенных в
объёме
-
мощность источников, заключенных в
объёме
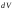 .
.
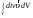 - алгебраическая мощность источников,
заключенных в объёме
- алгебраическая мощность источников,
заключенных в объёме
 .
.
Вследствие несжимаемости жидкости суммарная мощность источников должна равняться потоку жидкости, вытекающему наружу через поверхность S, ограничивающую объём V.
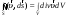
для любого
вектора
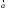 теорема
Остроградского-Гаусса выглядит:
теорема
Остроградского-Гаусса выглядит:
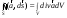
Теорема
Гаусса: 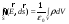
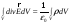
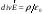 - дифференциальная форма теоремы Гаусса.
- дифференциальная форма теоремы Гаусса.
Нетрудно
доказать, что