
All lectures pdfs / Ур.мат.физ / Lecture_15 / 2011-03-17 / Лекция_15
.pdf
1
§15 Гармонические функции
внеограниченных областях
Вэтом параграфе мы познакомимся с некоторыми свойствами гармонических функций в неограниченных областях. Но сначала мы докажем одну важную теорему.
Теорема 1 (об устранении особенности)
Пусть функция u(x) гармонична в области - n fx0g, x0 2 - - некоторая точка (- ½ Rn - ограниченная область). Если при x ! x0: u(x) = o(U(x ¡ x0)), то
существует lim u(x) = A и функция u(x), доопределенная в т.x0 значением
x!x0
A, гармонична в -. Доказательство.
Пусть шар SR;x0 b -. Обозначим через v(x) классическое решение задачи Di в шаре SR;x0 :
R
x 0
½ 4xv(x) = 0; x 2 SR;x0 ;
vj@SR;x0 = uj@SR;x0 :
Функция w(x) = v(x) ¡ u(x) гармонична в области SR;x0 nfx0g и wj@SR;x0 = 0. Покажем, что w(x) = 0 в 8 т.x 2 SR;x0 n fx0g. Для этого рассмотрим две
функции (n>2):
§ w(x);
" > 0 - некоторое число.
Функции z§(x) - гармоничны в SR;x0 n fx0g и
|
|
z§j@SR;x0 = |
" |
> 0: |
|
|
|
|
|||
|
|
Rn¡2 |
|||
1 |
0 |
|
|
|
|
Т.к. u(x) = o( |
|
) при x ! x |
, то |
|
|
jx¡x0jn¡2 |
|
|
|||
" " µ 1 ¶
z§jjx¡x0j=½ = ½n¡2 § wjjx¡x0j=½ = ½n¡2 + o ½n¡2 :
Следовательно, при достаточно малых ½ > 0: z§jjx¡x0j=½ > 0. Согласно принципу максимума (см. x12):
z§(x) > 0 при ½ · jx ¡ x0j · R:
Возьмем теперь любую т.x1 2 SR;x0 n fx0g. Тогда существует такое достаточно малое число ½ > 0, что
|
x1 2 fx; ½ · jx ¡ x0j · Rg: |
||
Следовательно: |
z§(x1) > 0; |
|
|
т.е. |
|
||
" |
|
||
|
|
||
|
jw(x1)j < |
|
; |
|
jx1 ¡ x0jn¡2 |
||
2
откуда в силу произвольности выбора числа " > 0 следует, что
w(x1) = 0:
Итак, функция u(x) совпадает с функцией v(x) в области SR;x0 nfx0g. Доопределяя функцию u(x) в т.x0 значением A = v(x0), мы видим, что она совпадает с гармонической функцией v(x) во всем шаре SR;x0 , что и требовалось доказать.
Пусть - - неограниченная область из Rn, причем множество Rn n - содержит хотя бы одну внутреннюю точку, в которую мы поместим начало координат. Рассмотрим следующее взаимно-однозначное отображение области
Rn n f0g на себя: |
x |
|
|
|
x0 = |
|
: |
(1) |
|
jxj2 |
||||
|
|
|
Отображение (1) называется преобразованием инверсии (относительно сферы jxj = 1). Мы уже знакомы с преобразованием инверсии (см. x13). Отображение, обратное к (1) имеет вид, совершенно аналогичный (1):
|
|
|
|
|
x = |
x0 |
; |
(10) |
|
|
|
|
|
jx0j2 |
|||
|
|
|
|
|
|
|
|
|
т.е. (10) тоже преобразование инверсии. |
|
|
||||||
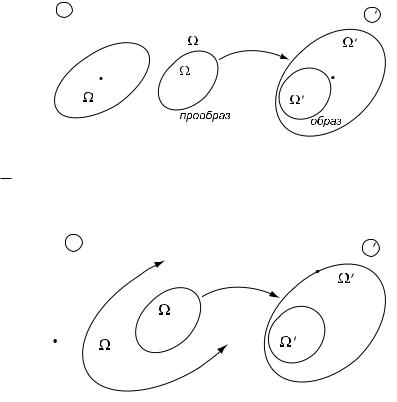
Два типа неограниченных областей: -1 b - |
|
|||||||
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
0 |
1 |
|
|
0 |
|
|
|
|
Rn \ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
) |
|
|
|
|
- |
|
|
|
|
|
|||
( n1 ½ |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
R n - - ограниченное множество. |
|
|
|
|||||
начало координат “0” - изолированная граничная точка области -0 @- -
x |
x |
|
|
|
0 |
|
(1) |
|
1 |
0 |
1 |
|
неограниченное множество начало координат "0"2 @-0
Пусть в области - задана функция u(x), x 2 -. Функция
u0(x0) = |
x0 |
1n¡2 uµ x00 |
2 |
¶; u0(x0) = Ke u(x) |
(2) |
|||
|
|
|
|
|
x |
|
|
|
j |
|
j |
|
j j |
|
|
|
|
определенная в области -0 называется преобразованием Кельвина функции u(x), x 2 -.
С учетом формул (1), (10), (2) легко получаем, что преобразование, обратное к преобразованию Кельвина, тоже есть преобразование Кельвина.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
В самом деле, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x = |
|
|
x0 |
|
; x0 = |
|
x |
|
; jxj = |
1 |
|
; |
||||
|
j |
x0 |
j |
2 |
|
x |
2 |
x0 |
j |
|||||||
|
|
|
|
|
|
j j |
|
|
|
|
j |
|
||||
то из (2) получаем: |
|
|
|
|
|
|
|
|
u0µ |
|
¶; |
|
|
|
||
|
u(x) = |
1 |
|
x |
|
|
(20) |
|||||||||
|
|
|
|
|
||||||||||||
|
jxjn¡2 |
jxj2 |
|
|
||||||||||||
т.е. u(x) = Ke u0(x0) и Ke ¢ Ke = I. Справедлива
Теорема 2.
Если u(x) гармоничная в -, то u0(x0) гармонична в -0. Доказательство.
Пусть -01 b -0, -1 - прообраз области -01 при преобразовании инверсии (1). Ясно, что -1 b - и -1 - ограниченная область. Функция u(x) по условию теоремы гармонична в -. Значит она гармоничная в -1 и u(x) 2 C2(-1). Как следует из x12 (см. теорему 1), для функции u(x) справедливо представление:
|
|
u(x) = Z ½u(») |
|
|
@N¡» |
¡ U(x ¡ ») |
|
@N» |
¾dS»: |
|
(¤) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
@U(x |
») |
|
|
|
|
|
|
|
@u(») |
|
|
|
|
|
|
||||||||
|
|
|
|
|
@-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В силу (2) имеем: |
|
|
|
|
¡ |
@Nj 0j |
»¡ |
|
¢ ¡ |
|
x0 n¡2 U |
µ x0 2 ¡ »¶ |
|
|
¾dS»: (¤¤) |
||||||||||||||||||||
u0(x0) = Z |
½u(») x0 n¡2 |
|
|
@N» |
|||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
@U |
x0 |
|
|
» |
|
|
|
|
1 |
|
|
|
|
x0 |
|
|
|
@u(») |
|
|
||||||
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
@-1 |
|
j |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
j |
|
|
|
|
j |
|
j |
|
|
|
|
|
|
|
|
Поскольку функция |
|
|
|
|
µjx0j¯jxx00j2 ¡ »¯ |
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n¡2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
¯ |
|
|
|
|
|
|||||||||||||||||||||||||||
с точностью до постоянного |
множителя¯ |
совпадает |
|
с функцией g1(x0; ») (см. |
|||||||||||||||||||||||||||||||
ничны по |
|
|
6 jx0j . |
¡Это |
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
© |
|
|
¡ |
x0 |
¢ª |
1 |
|||||||||
|
|
1 |
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@ |
|
|
|
1 |
|
|
|
|
|||||
x13), то функция |
jx0jn¡2 |
U |
|
jx0j2 |
|
¡ » |
|
и функция |
@N» |
|
|
jx0jn¡2 |
U |
jx0j2 |
¡ » |
гармо- |
|||||||||||||||||||
|
x0 |
при » = |
x0 |
|
|
|
|
|
означает, что u0(x0) гармонична в области -0 , а |
||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||
значит и в -0.
В дальнейшем будем рассматривать неограниченные области первого типа.
Определение.
Гармоническая в - функция u(x) называется регулярной на бесконечности, если
u(x) = o(1) (n > 2)
или
u(x) = o(ln jxj) (n = 2) при jxj ! 1:
Теорема 3.
Пусть функция u(x) гармонична в - и регулярна на бесконечности. Тогда
функция u0(x0) = Ke u(x) гармонична в -00 = -0 [ f0g. Доказательство.
В результате преобразования инверсии (1) область - переходит в область -0 (для которой начало координат - изолированная граничная точка).
В силу теоремы 2, u0(x0) = Ke u(x) гармоничная в -0. Кроме того
u0(x0) = x0 |
1n¡2 uµ x00 |
2 ¶ |
= o(jx0j2¡n) (n > 2) |
||||
|
|
|
|
x |
|
|
|
j |
j |
|
j j |
|
|
|
|
и
u0(x0) = o(ln jx0j) (n = 2) при x0 ! 0;
4
т.е.
u0(x0) = o(U(x0)); x0 ! 0
в силу регулярности на бесконечности функции u(x). Тогда по теореме 1 (об
устранении особенности) существует lim u0(x0) = A и функция u0(x0), доопре-
x0!0
деленная при x0 = 0 значением A, является гармонической в области -00.
Следующую теорему сформулируем без доказательства.
Теорема 4.
Пусть функция u(x) - гармонична в - и регулярна на бесконечности. Тогда существует постоянная R > 0 такая, что для 8x: jxj > R функция u(x) разлагается в абсолютно (и равномерно) сходящийся (вместе со всеми производными)
ряд |
|
|
|
|
|
|
x® |
|
|
|
|
||
|
u(x) = ® |
|
0 A® |
|
|
|
|
|
|||||
|
j¸ |
jxjn¡2+2j®j |
|
|
|
||||||||
|
jX |
|
|
|
|
|
|
|
|
|
|||
и имеют место неравенства |
|
|
|
|
|
|
|
|
|
|
|
||
¯Dx®u ¡ Dx®½ |
|
A0 |
¾¯ |
· |
|
|
C® |
; |
(3) |
||||
|
|
|
|
|
|
||||||||
¯ |
|
j |
j |
|
¯ |
j |
j |
|
|
|
|
||
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
где C® > 0 - некоторые постоянные.
Замечание.
Доказательство теоремы основано на том, что по теореме 3 u0(x0) = Ke u(x) гармонична в -00. В силу теоремы 6 из x12 функция u0(x0) в шаре jx0j < R0 разлагается в ряд Тейлора
|
|
jX |
|
|
|
|
|
1 |
|
|
|||
u0 |
(x0) = A®x0®; A® = |
®! |
D®u0(0): |
|
|||||||||
|
|
®j¸0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Но тогда для всех x: jxj > R = |
|
|
справедливо разложение |
|
|||||||||
R0 |
|
||||||||||||
u(x) = Ke u0(x0) = jxjn¡2 |
® |
|
0 A®µjxj2 |
¶ |
|
= ® 0 A® jxjn¡2+2j®j : |
|||||||
|
1 |
|
|
X |
x |
|
|
® |
jX |
x® |
|||
|
|
|
|
|
j |
j¸ |
|
|
|
|
|
j¸ |
|
Итак, с помощью преобразования Кельвина исследование гармонической функции в неограниченной области - может быть сведено к исследованию гармонической функции в ограниченной области -0.
Рассмотрим теперь задачу De: |
|
|
4xu = 0; x |
-; |
(4) |
½ uj@- = '(x); |
2x 2 @-: |
|
.
0
Что назвать классическим решением задачи (4)? Единственно ли классическое решение, если оно существует?

5
Заметим сразу, что в этом случае возникает проблема с единственностью решения задачи De (если не накладывать больше никаких ограничений на решение задачи De).
В самом деле, рассмотрим задачу De следующего вида (n = 2):
½ 4xu = 0; jxj > 1; ujjxj=1 = 0:
|
x2 |
0 |
1 |
|
|
|
x1 |
Очевидно, что функции
½ C ln r; C(rk ¡ r¡k) cos kµ;
C((rk ¡ r¡k) sin kµ; k = 1; 2; : : :
где r cos µ = x1, r sin µ = x2; C - произвольная постоянная, удовлетворяют задаче (40). Какую же из них принять за решение? Потребуем, чтобы решение задачи (4) было регулярно на бесконечности, т.е. u(x) = o(1) (n > 2) или u(x) = o(ln jxj) (n = 2) при jxj ! 1. Очевидно, что в случае задачи (40) из всего набора решений (¤) надо выбрать решение u ´ 0 которое и будет регулярным на бесконечности.
Теорема 5.
При любой непрерывной функции ' существует единственное классическое решение задачи De (4).
Доказательство.
Пусть u(x) 2 C2(-)\C(-) - классическое решение задачи De (4). Тогда функция u0(x0) - гармонична в области -00; кроме того
u0(x0)jx02@-00 = '0(x0) = Ke '(x); |
|
|||
u0(x0) 2 C2(-00 ) \ C( |
|
); |
|
|
-00 |
|
|
||
т.е. u0(x0) - классическое решение задачи Di |
|
|
||
4x0u0 = 0; x0 2 -00 ; |
|
(5) |
||
½ u0j@-00 = '0(x0); x0 2 @-00 |
: |
|
||
Итак, под классическим решением задачи De (4) мы будем понимать функцию u(x) 2 C2(-) \ C(-), гармоничную в области -, регулярную на бесконечности и принимающую на границе @- заданное значение '(x), x 2 @-
('(x) 2 C(@-)).
Принцип максимума в этом случае не работает!
Обратно, если u0(x0) - классическое решение задачи Di (5), то u(x) = Ke u0(x0) - гармонична в -, непрерывна в -, причем
uj@- = '(x);

6
регулярна на бесконечности (?), т.е. u(x) - классическое решение задачи (4). Значит, существование и единственность классического решения задачи
(4) вытекает из теоремы существования и единственности для задачи Di.
Задача.
Рассмотрим внешнюю третью краевую задачу
½ f@N |
+ ¾(x)ugj@- = '(x); x 2 @-: |
|
|||
xu = 0; |
x |
2 |
-; |
(6) |
|
4@u |
|
|
|
||
Покажите, что при ¾(x) ¸ 0 классическое решение задачи (6) единственно.
Указание.
u(x) 2 C2(-) \ C1(-) - классическое решение (u(x) - гармонична, регулярна на бесконечности). uI , uII - два решения, u = uI ¡ uII и т.д.
SR,0
R n \ 
|
-R = - \ SR;0 |
|
|
x12 |
К функциям v = u, u применим в области -R первую формулу Грина из |
||
0 = -RR u4udx = @R- u@N@u dS +jxjR=R u@N@u dS ¡-RR jruj2dx |
) |
||
|
-RR jruj2dx + @R- ¾u2dS = jxjR=R u@N@u dS: |
(+) |
|
Используя теорему 4 этого параграфа, покажите, что при R ! 1 правая |
|||
часть (+) стремится к 0 и (+) переходит в следующее: |
|
||
|
R jruj2dx + R ¾u2dS = 0: |
(++) |
|
|
- |
@- |
|
Пусть ¾(x) ¸ 0. Тогда из первого слагаемого вытекает, что u ´ const в -. При n > 2: u(x) = o(1) при jxj ! 1, т.е. u ´ 0 в -. При n = 2 и ¾(x) =6 0 равенство u ´ 0 вытекает из второго слагаемого. Если ¾(x) ´ 0 (задача Неймана), то при n > 2: u ´ 0 в силу регулярности на бесконечности, при n = 2 решение определяется с точностью до константы.
