
All lectures pdfs / Ур.мат.физ / Lecture_8 / 2010-10-28 / Лекция_8
.pdf
1
§8 Дополнительные сведения из функционального анализа
Пространства
Cm(-), Cm(-), C0m(-);
-½ RnS- ограниченное множество;
-= - @-- ограниченное замкнутое множество (компакт); suppf = fx 2 Rn; f(x) 6= 0g;
C0m(-) = ff(x) 2 Cm(-); suppf(x) b -g;
-1 b -, если -1 ½ - (-1 - подобласть, строго (целиком) лежащая в области -);
функция f(x) 2 C0m(-) - финитная функция;
C01(-)- множество бесконечно-дифференцируемых, финитных функций. Если - µ Rn - неограниченная область, то введем в рассмотрение про-
странство функций Bm(-) (это множество функций f(x), имеющих в области - непрерывные и ограниченные частные производные до порядка m включительно).
Пространства Cm(-), Bm(-) являются линейными нормированными пространствами. Дело в том, что на функциях из Cm(-) (или Bm(-)) можно определить функционал
½ |
f |
) = |
|
|
max |
j |
D®f(x) |
j |
|
( |
|
® |
j· |
m x2- |
x |
|
|||
|
|
|
jX |
|
|
|
|
||
|
|
|
jX |
D®f(x) |
|
|
|||
½(f) = |
|
|
sup |
|
; |
||||
µ |
|
|
®j·m x2- j |
|
x |
j¶ |
|||
обладающий следующими свойствами:
1)½(f) ¸ 0; ½(f) = 0 , f(x) ´ 0;
2)½(¸f) = j¸j½(f), где ¸ - любое вещественное число;
3)½(f + g) · ½(f) + ½(g) - неравенство треугольника.
В этом случае говорят, что пространство Cm(-) (Bm(-)) можно снабдить нормой
jjfjjCm( |
|
)(Bm(-)) = ½(f): |
(1) |
- |
Замечание.
1)Если - - ограниченная область из Rn, то Cm(-) ´ Bm(-).
2)Норма функции из C0(-) (B0(-)) - это некоторое положительное число, характеризующее тот факт, насколько функция f(x) отличается от нуля.
3)C0(-) = C(-), B0(-) = B(-).
Последовательность функций fk(x) 2 Cm(-) (Bm(-)) k = 1; 2; ::: называется сходящейся к функции f(x) 2 Cm(-) (Bm(-)) в пространстве Cm(-) (Bm(-)):
fk ! f; k ! 1 в Cm(-)(Bm(-);
если
½(fk ¡ f) ! 0; k ! 1:
Последовательность fk(x), k = 1; 2; ::: из Cm(-) (Bm(-)) называется фундаментальной в Cm(-) (Bm(-)), если
½(fk ¡ fp) ! 0; k; p ! 1:
Пространства Cm(-), Bm(-) являются полными, поскольку, если последовательность fk(x), k = 1; 2; ::: из Cm(-) (Bm(-)) фундаментальна в Cm(-) (Bm(-)), то существует функция f(x) 2 Cm(-) (Bm(-)) такая, что
½(fk ¡ f) ! 0; k ! 1:

2
Полное линейное нормированное пространство называется банаховым пространством.
Пусть - µ Rn. Совокупность всех комплекснозначных функций f(x), для которых функция jf(x)j2 интегрируема по области - (R jf(x)j2dx < 1) обо-
-
значим через L2(-).
Замечание.
Интегрирование вообще говоря понимается в смысле Лебега. L2(-) - линейное пространство.
Для любых f; g(x) 2 L2(-) справедливо неравенство Коши-Буняковского:
¯Z |
f(x)g(x)dx¯ · Z |
jf(x)jjg(x)jdx · µZ |
jf(x)j2dx¶2 |
µZ |
jg(x)j2dx¶2 |
: (2) |
|
¯- |
¯ |
- |
- |
1 |
- |
1 |
|
¯ |
¯ |
|
|
|
|
|
|
¯ |
¯ |
|
|
|
|
|
|
Если - - ограниченная область, g(x) ´ 1, то R dx = m(-) < 1 (мера
множества -) и |
|
|
- |
|
|
|
|
µZ jf(x)j2dx¶2 |
µZ dx¶2 |
< 1; |
|
¯Z f(x)dx¯ · Z jf(x)jdx · |
|||||
¯- |
¯ |
- |
1 |
1 |
|
- |
- |
|
|||
¯ |
¯ |
|
|
|
|
¯ |
¯ |
|
|
|
|
т.е. f(x) 2 L1(-), где L1(-) - множество интегрируемых функций (f(x)
L1 |
(-), если jf(x)jdx < 1). |
|
|
- |
|
|
На множествеR |
L2(-) введем скалярное произведение функций f; g(x) |
L2 |
(-): |
Z |
|
|
|
2
2
|
|
|
|
|
(3) |
(f; g)L2(-) = f(x)g(x)dx |
|
||||
- |
|
|
|
|
|
и норму функции f(x) 2 L2(-): |
jf(x)j2dx¶ |
|
|
||
½(f) = jjfjjL2(-) = (f; f)2 = µZ- |
: |
(4) |
|||
|
|
|
|
1 |
|
1 |
2 |
|
Тем самым L2(-) превращается в линейное нормированное пространство. Здесь g(x) - функция комплексно-сопряженная с g(x).
Замечание.
1) Скалярное произведение (3) обладает следующими очевидными свойствами:
а) (f; g)L2(-) = (g; f)L2(-),
б) (¸f + ¹g; h)L2(-) = ¸(f; h)L2(-) + ¹(g; h)L2(-).
Здесь f; g; h(x) 2 L2(-); ¸, ¹ - произвольные комплексные числа. 2) Неравенство (2) можно переписать так:
j(f; g)L2(-)j · jjfjjL2(-)jjgjjL2(-); f; g(x) 2 L2(-): |
(20) |
3) Легко проверить, что для нормы ½(f) = jjfjjL2(-) выполнены свойства: а) ½(f) ¸ 0,
½(f) = 0 , f = 0 почти всюду в - (т.е. f =6 0 только на множестве меры нуль);
б) ½(¸f) = j¸j½(f), ¸ - произвольное комплексное число;
в) ½(f + g) · ½(f) + ½(g) - неравенство Минковского (неравенство треугольника).
Здесь f; g(x) 2 L2(-).
3
Последовательность функций fk(x), k = 1; 2; ::: из L2(-) называется сходящейся к функции f(x) из L2(-) в пространстве L2(-) (или в среднем на -), если
½(fk ¡ f) ! 0; k ! 1 (fk ! f; k ! 1 в L2(-)):
Пространство L2(-) является полным в силу теоремы Рисса-Фишера.
Теорема Рисса-Фишера.
Если последовательность функций fk(x), k = 1; 2; ::: из L2(-) является фундаментальной в L2(-) (т.е. ½(fk¡fp) ! 0; k; p ! 1), то существует единственная (с точностью до значений на множестве меры нуль) функция f(x) из L2(-) такая, что:
½(fk ¡ f) ! 0; k ! 1:
Итак, L2(-) - банахово пространство со скалярным произведением (2) (гильбертово пространство).
Как можно еще определить пространство L2(-)?
Определение.
Множество функций M ½ L2(-) называется плотным в L2(-), если для любой функции f(x) 2 L2(-) существует последовательность функций fk(x), k = 1; 2; ::: из M такая, что
½(fk ¡ f) ! 0; k ! 1
(½(f) = jjfjjL2(-)):
Лемма.
Множество C01(-) плотно в L2(-).
Здесь C01(-) = ff(x) 2 C1(-); suppf b -g.
Итак, множество L2(-) является замыканием множества C01(-) в норме ½(f) = jjfjjL2(-) (L2(-) = C01(-)+ все предельные функции, полученные по
норме L2(-)).
Замечание.
Можно ввести в рассмотрение и так называемые весовые пространства L2;k(-) с нормой:
½(f) = jjfjjL2;k(-) = µZ- |
jf(x)j2(1 + jxj2)kdx¶2 |
; k ? 0: |
|
1 |
|
Множество C01(-) плотно в L2;k(-) (C01(-) ½ L2;k(-)). L2;k(-) - гильбертово пространство.
Задача.
Как определяется скалярное произведение в L2;k(-)? Замыкая множество C01(-) по норме
½(f) = µZ |
® m jDx®f(x)j2dx¶ |
; |
(5) |
|
jX |
1 |
|
|
|
2 |
|
- |
j· |
|
|
можно определить так называемые пространства Соболева W2m(-), m ¸ 0 - целое число (W20 = L2).
Пространство W2m(-) это множество функций f(x) 2 L2(-), все производные которых до порядка m включительно принадлежат L2(-).
W2m(-) - гильбертово пространство с нормой (5)
½(f) = jjfjjW2m(-) = µ X jjDx®f(x)jjL2 2(-)¶ |
: |
(50) |
|
1 |
|
|
2 |
|
j®j·m
4
Множество C01(-) плотно в W2m(-) (C01(-) ½ W2m(-)). Сходимость в W2m(-)
по норме: ½(fk ¡ f) ! 0, k ! 1, fk(x) 2 W2m(-), k = 1; 2; :::, f(x) 2 W2m(-).
Задача.
Скалярное произведение в W2m(-)? Пусть - = Rn.
Введем в рассмотрение пространство J ff(x) 2 C1(Rn); (1+jxj2)kjDx®f(x)j !
0 при jxj ! 1; k; ® = (®1; :::; ®n); ®j ¸ 0; k ¸ 0 - любыеg
P(jxj)jDx®f(x)j ! 0, P(jxj) - любой полином от jxj.
e¡jxj2 2 J .
Поскольку C01(Rn) ½ J , то J плотно в L2(Rn), L2;k(Rn), k ? 0, W2m(Rn). f(t; x) 2 L2(G), G ½ Rn+1.
C([0; T ]; L2(-)) - пространство функций f(t; x) непрерывных по t на [0; T ] в L2(-) с нормой
|
|
|
|
|
|
µZ- |
|
|
|
¶ |
1 |
|
|
|
|
|
|
|
|
2dx |
2 |
||
½ |
f |
|
f |
|
max |
f |
t; x |
: |
|||
( |
|
) = jj |
|
jjC(¢) = |
0·t·T |
j ( |
|
)j |
|
Сходимость в C([ ]; L2(-))
½(fk ¡ f) ! 0; k ! 1:
Справедлив аналог теоремы Рисса-Фишера: если ffk(t; x)g, k = 1; 2; :::, fk(t; x) 2 C(¢) фундаментальна в C(¢), то существует функция f(t; x) 2 C(¢) такая, что
½(fk ¡ f) ! 0; k ! 1:
Теорема Фубини (о перемене порядка интегрирования).
Если функция f(x; y), заданная в Rn+m, x 2 Rn, y 2 Rm измерима и существует повторный интеграл функции jf(x; y)j
m |
· n jf(x; y)jdx¸dy < 1; |
RZ |
RZ |
то f(x; y) интегрируема. Если f(x; y) интегрируема, то интегралы
|
|
Z |
|
Z |
|
|
|
f(x; y)dx; |
f(x; y)dy |
|
|
|
|
Rn |
|
Rm |
|
существуют почти везде и интегрируемы, причем |
|
||||
R |
nZ+m |
f(x; y)dxdy = Zn |
·Zm f(x; y)dy¸dx = Zm |
·Zn f(x; y)dx¸dy |
|
|
R |
R |
R |
R |
|
(функция f называется измеримой, если она совпадает почти везде с пределом почти везде сходящейся последовательности кусочно-непрерывных функций).
Интегрируемая функция?
Весовое пространство L2;k(-): если - - ограниченное множество, то L2;k(-) =
L2(-).
f(x) = e¡x12 ,
f(x) 2 C1(¢), Dx®f(x)jx=0 = 0,
0
f(x) не аналитична в точке x = 0:
5
f(x) = P fkxk ´ 0, чего быть не может.
k¸0
1
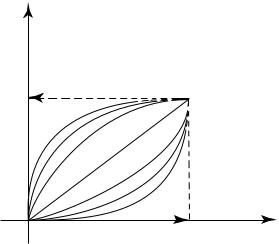
fn(x) = xn , 0 · x · 1, n = 1; 2; :::, fn fen(x) = xn, 0 · x · 1, n = 1; 2; :::, fen
fn ! 1 п.в. (в L2(0; 1)), fen ! 0 п.в. (в L2(0; 1)).
фундаментальна в L2, фундаментальна в L2,
1
0 |
1 |
x |
|
