
All lectures pdfs / Диф.уравнения / Лекция_1
.pdf§1. Предварительные сведения
Известно, что при математическом моделировании физических процессов в науке и технике возникают самые различные
обыкновенные дифференциальные уравнения.
Теория дифференциальных уравнений - это раздел математики, который изучает математические модели различных физических (а, также, биологических, химических, геологических и т.д.) явлений.
Теория обыкновенных дифференциальных уравнений - это часть более общей математической дисциплины: теории дифференциальных уравнений.
Для того, чтобы определиться с объектами, которые изучаются
внашем курсе, дадим следующее определение.
Определение 1
I. Обыкновенным дифференциальным уравнением n-го порядка называется соотношение вида
F (t; y; y0; y00; :::; y(n)) = 0 |
(1) |
между независимой переменной t 2 R1, её функцией y(t), производными от этой функции (до порядка n включительно).
II. Решением дифференциального уравнения n-го порядка (1) на (a; b) ((a; b) - интервал, принадлежащий R1) называется функция y = '(t), определенная на интервале (a; b) вместе со своими производными до n-го порядка включительно, и, такая, что подстановка функции y = '(t) в (1) превращает последнее в тождество по t на интервале (a; b).
Простейшими примерами обыкновенных дифференциальных
1
Лекция №1, НГУ, ММФ, 2009 |
2 |
уравнений (а, именно с этих примеров мы начнем изучение теории обыкновенных дифференциальных уравнений в нашем курсе) являются так называемые линейные уравнения с постоянными коэффициентами, т.е. когда в (1) функция F линейна по отношению к y; y0; :::; y(n):
Ly = y(n) + a1y(n¡1) + ::: + an¡1y0 + any = 0; |
(2) |
причем коэффициенты a1; :::; an - некоторые постоянные (вещественные или комплексные). Кроме этого, мы обозначили в (2) через L дифференциальный оператор
|
dn |
dn¡1 |
d |
|
|
|||
L = |
|
+ a1 |
|
+ ::: + an¡1 |
|
|
+ an; |
(3) |
n |
n 1 |
dt |
||||||
|
dt |
dt ¡ |
|
|
||||
действующий на функцию y = y(t).
Итак (2) - это линейное однородное обыкновенное дифференциальное уравнение порядка n с постоянными коэффициентами. Если вместо (2) мы рассматриваем уравнение с
правой частью |
|
Ly = f(t); |
(4) |
где f = f(t) - известная функция от t, то уравнение (4) - линейное неоднородное.
Пример 1. Найти такие кривые на плоскости (t; y), чтобы тангенс угла наклона касательной (по отношению к оси абсцисс) в любой точке этих кривых равнялся бы ординате y этой точки, умноженной на некоторое вещественное число a (см. Рис. 1). Поскольку tg® = y0, то функция y = y(t) удовлетворяет линейному однородному дифференциальному уравнению первого порядка
y0 = ay:
Это уравнение можно переписать так
(e¡aty)0 = 0;
т.е.
e¡aty(t) = C;
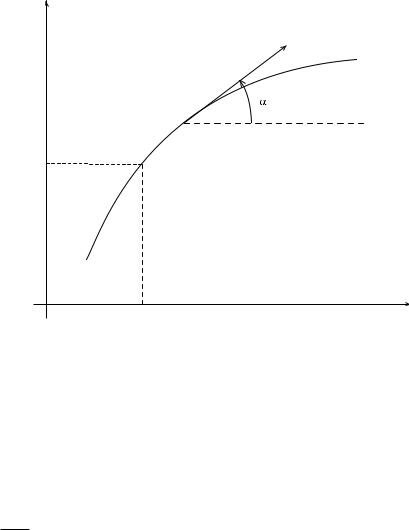
Лекция №1, НГУ, ММФ, 2009 |
3 |
y
y=y(t)
y0
t
0 |
t0 |
Рис. 1:
где C - произвольная вещественная постоянная. Следовательно, уравнение кривых с нужным для нас свойством записывается в таком виде:
y = y(t) = Ceat: |
(5) |
Определение 2. Решение дифференциального уравнения n-го порядка (1), зависящее от n произвольных постоянных
Ci; i = 1; n:
y = '(t; C1; :::; Cn)
называется общим решением этого уравнения. Следовательно в случае примера 1 формула (5) задает общее
решение уравнения y0 = ay.
Определение 3. Задачей Коши для (1) называется задача о нахождении на интервале (a; b), так называемого частного решения y = '(t) уравнения (1), удовлетворяющего n начальным условиям при t = t0; t0 2 (a; b):
'(t0) = '0; '0(t0) = '1; :::; '(n¡1)(t0) = 'n¡1;
Лекция №1, НГУ, ММФ, 2009 |
|
|
|
|
4 |
где '0; '1; :::; 'n¡1 - некоторые заданные постоянные. |
|
||||
Для уравнения y0 = ay Задача Коши формулируется так |
|
||||
(З.К.) |
y0 = ay; t |
(a; b); |
(6) |
||
(y(t0) = y0 |
;2t0 |
2 |
(a; b); |
||
|
|
|
|
|
|
где y0 - некоторая заданная постоянная. Легко видеть, что имея на руках формулу общего решения (5) уравнения y0 = ay, можно решить Задачу Коши (6). В самом деле, полагая в (5) t = t0, мы
получаем, что
C = y0e¡at0;
т.е. искомое решение Задачи Коши (6) имеет следующий вид:
y = y0ea(t¡t0): |
(7) |
Геометрический смысл решения Задачи Коши (6) ясен: из всех кривых, описываемых формулой (5) надо выбрать такую, которая проходит через заданную точку (t0; y0) (см. формулу (7) и Рис. 1). Заметим, что решение Задачи Коши (6) определено при всех t 2 R1, а также для любых t0 2 R1; y0 2 R1.
Наряду с одним уравнением порядка n мы будем в нашем курсе рассматривать и системы обыкновенных дифференциальных уравнений. Мы не будем приводить здесь строгого определения таких систем, а ограничимся рассмотрением нескольких важных примеров систем дифференциальных уравнений.
Пример 2. Рассмотрим систему следующего вида: |
|
||
y10 |
= ¡y2 |
; |
|
(y20 |
= y1: |
|
(8) |
Здесь y1;2 = y1;2(t) - неизвестные функции. Обозначим через y(t)
вектор-функцию с компонентами y1;2(t):
à !
y(t) = y1(t) : y2(t)

Лекция №1, НГУ, ММФ, 2009 |
5 |
В таком случае (8) удобно переписать в так называемом вектор-
ном виде: |
= dt = Ãy20 ! |
= Ã1 ¡0!Ãy2! = Ã1 ¡0!y |
|||
y0 = Ãy2! |
|||||
y1 |
0 |
dy |
y10 |
0 1 y1 |
0 1 |
|
|||||
или
y0 = Ay;
Ã!
где A = |
0 |
¡1 |
- квадратная матрица порядка 2. |
|
1 |
0 |
|
В общем случае систему линейных уравнений с постоянными коэффициентами для N неизвестных функций y1(t); :::; yN (t) за-
пишем в таком же векторном виде: |
|
|
|
|
||||||
|
|
|
y0 = |
dy |
= Ay; |
(9) |
||||
|
|
|
|
|||||||
где |
|
|
|
|
dt |
|
|
|
|
|
0 |
.y1 1 |
|
0:a:11: : ::: |
:::: : :a:1N: :1 |
|
|
|
|||
y = |
; A = (aij) = |
; i; j = 1; N; |
||||||||
|
@ |
A |
|
@ |
|
A |
|
|
|
|
|
ByN C |
|
|
aN1 : : : aNN |
|
|
|
|||
aij - элементы матрицы A, вещественные (или комплексные) числа. Покомпонентная запись системы (9) состоит, естественно, из N уравнений следующего вида:
dyi dt
Понятно, что (90) - однородная система, система же
dydt = Ay + f(t);
0f1(t) 1
где f(t) = B@. CA - заданная вектор-функция, неоднородная. fN (t)

Лекция №1, НГУ, ММФ, 2009 |
6 |
Наконец, наряду с (9), (10) будем рассматривать так называе-
мые матричные уравнения |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dY |
= AY; |
(11) |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
где неизвестные (искомые) функции объединены в матрицу |
|
||||||||||||||||
|
|
|
|
0:y:11: (:t:): : ::::::: :y:1:N:(:t:):1; i; j = |
|
; |
|
||||||||||
Y = (yij) = |
1; N |
|
|||||||||||||||
|
|
|
|
@yN1(t) : : : yNN (t)A |
|
||||||||||||
при этом, по определению |
|
|
|
|
|
|
|
|
|
|
|
||||||
dY |
|
y110 |
|
: : : y10 |
N |
|
|
|
|||||||||
@yN0 |
1 |
|
: : : yN0 N A |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
dt = 0: : : : : : : : : : : : :1; i; j = 1; N: |
|
|||||||||||||||
Покомпонентная запись системы (11) такова: |
|
||||||||||||||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
||
|
|
dyir |
|
Xj |
|
|
|
|
|
|
|
(110) |
|||||
|
|
= |
|
|
aijyjr; i; r = 1; N: |
||||||||||||
|
|
|
dt |
|
|
||||||||||||
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из (110) следует, что на самом деле систему (11) можно переписать в векторном виде. Действительно, обозначим через y[k](t); k = 1; N следующие вектор-функции:
|
y[1] = |
0 |
.y11 |
1 |
; :::; y[N] = |
0.y1N |
1: |
|
|
|||||||||
|
|
|
ByN1C |
|
|
|
|
ByNN C |
|
|
||||||||
|
|
|
@ |
|
|
A |
|
|
|
|
@ |
|
A |
|
|
|||
Тогда из (110) следует, что: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dy[k] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Ay[k]; k = 1; N |
|
|
|
||||||||||
или |
|
|
dt |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
1 |
. |
|
|
|
||||||
dt . |
|
|
|
|
|
|
|
|
|
|||||||||
|
d |
0y[1] |
1 |
= |
|
A ... |
0 |
|
|
|
0y[1] |
1 |
; |
(1100) |
||||
|
|
|
A |
|
|
|
||||||||||||
|
|
By[N]C |
|
|
|
0 |
|
|
|
By[N]C |
|
|
||||||
|
|
B |
|
|
C |
|
|
@ |
|
AB |
C |
|
|
|||||
|
|
@ |
|
|
A |
|
|
|
|
|
|
|
|
@ |
|
A |
|
|

Лекция №1, НГУ, ММФ, 2009 |
7 |
т.е. вместо (11) мы получили вновь систему вида (9).
Перейдем теперь к заключительной части этого параграфа, в которой приведем некоторые, необходимые нам в будущем, сведения из теории матриц. Пусть, как обычно, RN ¡ N-мерное вещественное евклидово пространство, CN ¡ N-мерное комплексное
пространство. Далее, пусть мы имеем вектор-функцию
0y1(t) 1
y = B@. CA; причем при любом t 2 R1 : y(t) 2 RN (или CN ).
yN (t)
Как известно, для векторов из RN (или CN ) можно ввести длину (норму):
y |
= y(t) |
|
= (y; y) = v |
|
|
|
при любом t R1: (12) |
|||||||
|
N |
yi 2 |
||||||||||||
|
|
|
|
p |
|
|
uX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
jj jj |
jj |
|
jj |
|
|
|
ui=1 j |
|
j |
|
|
2 |
||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
yixi ¡ скалярное произведение векторов |
|||||||||||
(y; x) = |
||||||||||||||
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi |
|
|
0 |
.y1 1; x = |
0 |
.x1 1 |
|
|
||||
|
|
|
|
y = |
: |
|
||||||||
|
|
|
|
|
|
ByN C |
|
BxN C |
|
|
||||
|
|
|
|
|
|
@ |
A |
|
@ |
A |
|
|
||
Заметим, что мы привели формулу для скалярного произведения векторов в общем случае, когда x; y 2 CN . Напомним, что скалярное произведение векторов x; y обладает следующими очевидными свойствами:
а) (y; x) = (x; y), где черта сверху обозначает комплексное сопряжение;
б) (®y; x) = ®(y; x); ® 2 C1; в) (y; ®x) = ®(y; x); ® 2 C1; г) jjyjj = 0 , y = 0:

Лекция №1, НГУ, ММФ, 2009 |
8 |
В нашем курсе мы часто будем пользоваться известными неравенствами Куранта:
¸min(B)jjyjj2 · (By; y) · ¸max(B)jjyjj2; |
(13) |
где B = B¤ - эрмитова матрица (B = (bij); B¤ = (bji); i; j = 1; N), ¸min(B); ¸max(B) - наименьшее и наибольшее собственные числа эрмитовой матрицы B. Заметим, что все собственные числа
эрмитовой матрицы B вещественные. Докажем неравенства (13). С этой целью вспомним известное утверждение из теории матриц о том, что любая эрмитова матрица B может быть приведена к
диагональному виду с помощью некоторого унитарного преобразования U = U(B) (U¡1 = U¤): B = U¤DU; D = diag(¸1; :::; ¸N );
где ¸i = ¸i(B); i = 1; N - собственные числа матрицы B, при-
чем ¸1 = ¸min(B); ¸N = ¸max(B). Тогда (By; y) = (U¤DUy; y) = (DUy; Uy) = ¸1jz1j2 + ::: + ¸N jzN j2, где
0z1 1
z = B@. CA = Uy: zN
С другой стороны
|
N |
|
¸1jjzjj2 · |
Xi |
|
¸ijzij2 · ¸N jjzjj2 |
(14) |
|
|
=1 |
|
(мы считаем, что диагональные элементы матрицы D расположены в порядке возрастания). Поскольку
jjzjj2 = (z; z) = (Uy; Uy) = (U¤Uy; y) = (y; y) = jjyjj;
то из (14) следуют неравенства (13), что и требовалось доказать. Кроме нормы (длины) вектора y 2 RN (или CN ) можно ввести, также, норму матрицы A = (aij); i; j = 1; N. В теории матриц даются определения различных норм матрицы A. Наиболее ходовыми являются: операторная и эвклидова нормы матрицы A

Лекция №1, НГУ, ММФ, 2009 |
9 |
(последняя называется еще Фробениусовой нормой матрицы
A).
Определение 4. Операторной нормой матрицы A называют
величину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
= sup |
|
Ay |
|
|
= |
sup |
(Ay; Ay) |
: |
(15) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
jj |
jj |
jj |
|
y |
|
jj |
(y; y) |
|||||||||
|
y=0 |
|
|
|
sy=0 |
|
|
|||||||||
|
|
|
6 |
jj |
|
jj |
|
6 |
|
|
|
|
||||
Заметим однако, что исходя из определения 4 очень трудно вычислить норму конкретной матрицы A. С этой целью преобразуем правую часть формулы (15):
|
|
(Ay; Ay) |
|
|
(A¤Ay; y) |
|
|
|
|||
sup |
= sup |
= max(A¤Az; z) = |
|||||||||
|
|
|
|
||||||||
sy6=0 |
(y; y) |
sy6=0 |
(y; y) |
rjjzjj=1 |
|||||||
r
=max(A¤Ay; y):
jjyjj=1
В приведенной здесь цепочке преобразований мы вначале сделали замену z = jjyyjj, а потом вернулись к прежнему обозначению:
y = z. Понятно, что матрица A¤A - эрмитова и A¤A ¸ 0, поскольку эрмитова форма
(A¤Ay; y) = (Ay; Ay) = jjAyjj2 ¸ 0:
Заметим далее, что эрмитова форма (A¤Ay; y) - непрерывная функция от y, определенная на компакте jjyjj = 1. Поэтому она достигает на этом множестве своего максимального и своего минимального значений. При этом в силу (13)
max(A¤Ay; y) = ¸ |
max |
(A¤A) |
¸ |
0: |
|||
y =1 |
|
|
|
|
|
||
jj jj |
|
|
|
|
|
|
|
Таким образом, окончательно получаем |
|
|
|||||
jjAjj = |
p |
|
|
|
|
|
|
¸max(A¤A) ¸ 0: |
(16) |
||||||
В отличии от операторной нормы матрицы A Фробениусова нор-
Лекция №1, НГУ, ММФ, 2009 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
||||||||
ма вводится так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
uX |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A |
|
|
|
|
t |
|
|
|
aij 2: |
|
|
|
|
(17) |
|||||
|
|
|
|
|
|
|
E = v N |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
jj |
jj |
|
|
ui;j=1 j |
j |
|
|
|
|
|
|
||||||||
Покажем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
jjAjj · jjAjjE: |
|
|
|
|
(18) |
|||||||||||
С этой целью напомним вначале известное неравенство |
|
|
|||||||||||||||||||||||
Буняковского-Шварца: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
j(x; y)j2 · (x; x)(y; y); |
|
|
|
|
(19) |
||||||||||||||
где x; y 2 RN (или CN ). Далее, поскольку |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ui=1 |
Ãj=1 |
|
!Ãj=1 |
|
|
! |
||||||||
|
|
ui=1 |
ïj=1 |
|
¯! |
|
|
|
|
|
|||||||||||||||
Ay = v N |
|
N aijyj |
¯ |
2 |
|
|
|
|
|
|
N |
N |
aij 2 |
N |
|
yj |
2 = |
||||||||
|
|
uX |
¯X |
|
|
|
|
uX X |
|
X |
|
|
|
|
|||||||||||
jj jj |
t |
¯ |
|
|
|
|
¯ |
|
|
|
t |
|
|
|
j j |
|
j |
|
j |
||||||
u |
¯ |
|
|
|
|
¯ |
|
|
· v |
|
|
|
|
|
|||||||||||
= |
y |
A |
; ¯ |
|
jjAyjj |
|
¯ |
|
|
A |
|
|
; |
|
|
|
|
|
|
|
|
|
|
||
|
jj |
jj ¢ jj jjE |
то |
jjyjj |
|
|
· jj |
|
jjE |
|
|
что и требовалось доказать. |
|||||||||||||
Наконец, в конце параграфа, в качестве упражнения докажем
неравенство: |
|
|
|
|
|
jjABjj · jjAjj ¢ jjBjj; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(20) |
||||||||
где A; B - квадратные матрицы порядка N. |
|
|
|
|
|
|
|||||||||||||||
В самом деле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
(ABy; ABy) |
|
|
|
|
|
||||||||||
jj |
AB |
jj |
= |
|
sup |
= |
|
max(A¤ABy; By) |
· |
||||||||||||
|
|
||||||||||||||||||||
|
|
sy6=0 |
|
|
|
jjyjj2 |
rjjyjj=1 |
|
|
|
|
|
|||||||||
|
|
|
|
max |
¸ |
|
(A¤A)(By; By) |
g |
= |
jj |
A |
jj ¢ jj |
B : |
|
|||||||
|
· rjjyjj=1f |
|
|
max |
|
|
|
|
|
|
|
jj |
|
||||||||
