
Lektsii_po_Diskretnoy_Matematike / Глава 4
.pdf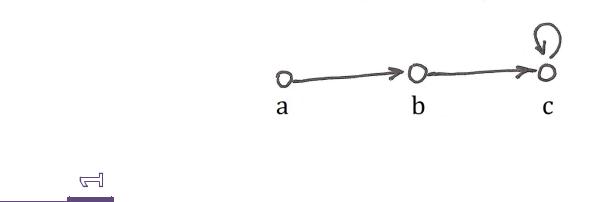
|
|
|
|
|
|
|
Глава 4. Теорияотношений. |
|
|
|
|
|
|
Глава 4 |
||||||||||||||||||
Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 × 2 |
× … × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
местное) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Определение. Отношение (Введениеn- |
. – это множество упорядоченных |
|||||||||||||||||||||||||||||
n-ок |
|
|
1, |
× 2 × … × |
|
|
|
|
1 = 2 |
= = |
|
|
|
|
|
задано на |
||||||||||||||||
|
такое, |
что |
|
|
|
|
|
|
|
|
|
. При этом говорят, что |
|
|||||||||||||||||||
множестве |
|
|
|
|
|
. Если |
|
|
|
|
|
|
|
|
, |
то отношение называют |
||||||||||||||||
односортным если иначе – многосортным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
// |
|
|
1 |
× 2 × … × |
|
|
|
|
. |
|
что |
|
является подмножеством |
|||||||||||||||||||
//Запись |
|
|
|
|
|
|
|
|
|
означает, |
|
|
|
|||||||||||||||||||
|
декартова произведения |
|
|
|
|
|
= |
{(1,1), |
(2,2), … }, где 1 = и 2 |
= . |
||||||||||||||||||||||
Односортные – отношения равенства |
||||||||||||||||||||||||||||||||
|
|
Пример. Многосортные1 |
×отношения2 × … ×– это |
отношения в реляционной алгебре. |
||||||||||||||||||||||||||||
|
|
Определение. Бинарное отношение – это отношение |
|
|
|
|
, где |
|
|
– |
||||||||||||||||||||||
бинарного отношения. |
|
бинарного отношения, |
2 |
– |
область |
изменения |
|
|||||||||||||||||||||||||
область |
определения |
|
|
|
1 |
× 2 |
|
|
|
1 |
|
|||||||||||||||||||||
|
|
Формы записи бинарных отношений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) |
На множествах – |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Инфиксная форма – |
|
|
. |
|
.( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3) |
1. |
|
|
|
, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
В виде предиката(отношения, ) |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2. |
( , ) = |
1, если |
( , ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1) |
Пусть( дано, ) = |
0некоторое( , отношение) |
|
на |
множестве |
= { , , } |
. |
Тогда |
|||||||||||||||||||||||
|
Прямое перечисление – |
{( , ), ( , ), |
( , )}. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
существуют следующие способы задания |
отношений: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2) |
Граф (здесь ( , ) и ( , ) – это дуги). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

Кононов Василий, Сагитова Адиля и Главатских Павел |
Глава 4 |
3) Матрица:
0 |
1 |
0 |
|
|
|
0 |
0 |
1 |
|
|
|
0 |
0 |
1 |
|
|
|
4) |
«На фактор-множествах» – задание через окрестности вершин в графе: |
|||||||||||||
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
{ } |
{ } |
{ } |
|
|
|
|
|
|
||В верхней части располагаются элементы из множества |
|
(вершины графа), а в |
||||||||||||
||нижней – |
окрестности |
– подмножества элементов |
множества |
, |
которые |
|||||||||
|
|
|
|
|
||||||||||
||непосредственно достижимы из соответствующей вершины. |
|
|||||||||||||
|
|
|
|
Форма записи операций. |
|
|
|
|
|
|||||
|
Пусть есть операция + . Тогда существуют различные её формы записи: |
|||||||||||||
1) |
+ , |
– префиксная форма. |
|
|
|
|
|
|
|
|
|
|
||
2) |
– инфиксная форма. |
|
|
|
|
|
|
|
|
|
|
|||
3) |
+ |
– постфиксная форма. |
|
|
|
|
|
|
|
|
|
|||
||Польская, +нотация – это префиксная форма записи. Обратная польская нотация – |
||||||||||||||
||это постфиксная форма записи. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
свойств отношения достаточно знать только его структуру |
|||||||||||
|
Для исследования |
|
Изоморфизм отношений. |
|
|
|
|
|
||||||
(например, |
задаваемую |
дугами |
|
в графе), |
при этом |
обозначения |
вершин |
|||||||
(конкретный состав множеств) нам не важен. |
|
|
|
|
|
|
|
|||||||
|
Для × и × |
существует : → такое, что |
|
|
||||||||||
|
|
, → ( ), , |
|
|
|
|||||||||
и, в обратную сторону:( 1, 2) → −1( 1), −1( 2) .

|
|
→ |
|
|
– это обратное |
|
|
|
|
|
|
||||||
Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
|
Глава 4 |
||||||||||||
||” |
: |
|
|
−1 |
|
|
|
|
|
|
|
|
во множество |
|
. При этом, |
|
– это |
|
” – это отображение множества |
|
|
|
|||||||||||||
||прямое отображение, |
|
|
|
|
|
|
|
отображение. |
|
|
|
|
|||||
|
|
Эти формулы означают |
, что всегда можно провести взаимно-однозначное |
||||||||||||||
соответствие вершин отношений |
и |
|
, если они имеют одинаковую структуру. |
||||||||||||||
|
|
|
|
Операции над отношениями. |
|
|
|
|
|||||||||
Далее можно отвлечься от имён |
работать |
олько со структурой. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Как и |
в реляционной |
алгебре, |
над |
отношениями |
существует |
2 типа |
|||||||||
1)Теоретико-множественные операции – объединение , пресечение ∩ и
разность .операций:
2) Специальные операции: |
{( , )|( , ) }, где −1 × . |
|
|
|||||||||||||||
1. |
|
|
|
|
−1 |
= |
|
|
||||||||||
Обратное отношение – для бинарного отношения × – это: |
|
|||||||||||||||||
||Обратное |
отношение |
|
−1 |
состоит |
из |
пар |
( , ) |
таких, что пары |
( , ) |
|||||||||
||принадлежат отношению |
|
. |
|
|
|
|
|
|
|
|||||||||
2. |
Дополнение: |
|
|
|
|
|
где |
|
|
|
. |
|
|
|
||||
3. |
× – это: = {( , )| }, где 2. |
|
|
|
|
|
||||||||||||
Тождественное |
=отношение{( , )|( , –) для},односортного× бинарного отношения |
|||||||||||||||||
4. |
|
|
|
|
= |
{( , )| и }, где = × . |
|
|
||||||||||
Универсальное отношение – для отношения |
× – это: |
|
||||||||||||||||
5. |
Композиция отношений 1 |
× и 2 |
× – это отношение |
|
||||||||||||||
|
Пример= 1 . Пусть2 = {( есть, )| 2 отношения, и – 2 |
1 } |
где × и. |
|||||||||||||||
|
2 = {( , ), ( , ), ( , )}, тогда их |
1 = {( , ), ( , ), |
( , ), ( , )} |
|||||||||||||||
|
|
|
|
|
= |
= |
|
композиция – это отношение |
|
|||||||||
||Чтобы |
составить |
|
, , , , |
, , , . |
|
|
||||||||||||
||месте во 2-м1 |
отношении: |
, |
2 |
|
|
|
|
|
все) ( |
пары)} |
элементов в |
|||||||
|
|
|
|
композицию1 |
{(, рассмотрим) ( ) ( |
|||||||||||||
||отношении |
|
. 1-я пара – |
|
|
|
|
2-й элемент – . Значит, ищем его на 1-м |
|||||||||||
|
|
|
, здесь1 2 |
. Т.е. надо найти пары, у которых |
||||||||||||||
|
|
|
|
|
|
|
это пара |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
соответственно. Следовательно, 1-я пара в |
||||||||
||совпадают последний и 1-й элементы , |
|
|
|
|
|
|
|
|||||||||||
||композиции такая: |
( , ). И так далее. |
|
|
|
|
|
|
|
|
|
||||||||
Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
Глава 4 |
||
6. |
Степень отношения: = × × … × ( |
раз). |
|
|||
7. |
Ядро отношения: ker = −1. |
|
|
. |
|
|
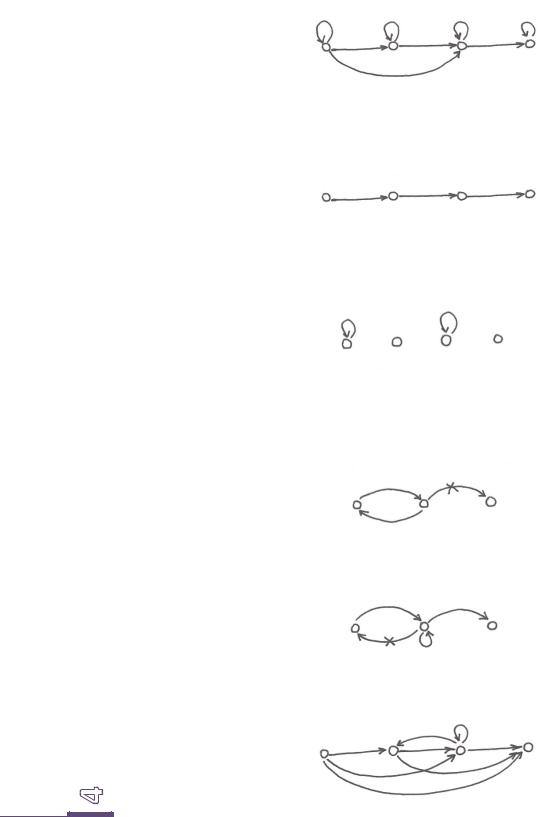
1) Рефлексивные – для |
Классы отношений, |
|
||||
|
|
( , ) |
где |
× |
. |
|
|
|
|
|
|
||
2) Иррефлексивные – для ( , ) , где × .
3) Нерефлексивные – ( , ) и ( , ) .
||Т.е. существуют пары,(принадлежащие) ( ) , и пары, не принадлежащие . 4) Симметричные – , , .
5) Антисимметричные – для , → ( , ) ( , ) ( = ).
6) Транзитивные – ( , ) , ( , ) ( , ) .
7) Интранзитивные – ( , ) , ( , ) ( , ) . |
Глава 4 |
Кононов Василий, Сагитова Адиля и Главатских Павел |
Влияние операций над отношениями на различные классы отношений:
−1 |
1 |
2 |
Рефлексивные
Иррефлексивные
Симметричные
Антисимметричные
Транзитивные
Покажем, что объединение транзитивных отношений не всегда является транзитивным отношением. Пусть даны 2 транзитивных отношения:
В результате объединения отношений получается следующее отношение:
Оно не является транзитивным, т.к. нет связи между вершинами и .
Отношения также применимы и в реляционных базах данных, в которых одной из практических задач является оценка объёмов данных в таблице. В области отношений есть аналогичная задача – оценка количества различных бинарных отношений. Она является частным случаем оценки количества 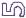 n-местных отношений.
n-местных отношений.

Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
Глава 4 |
||
Пусть есть произвольное бинарное |
отношение |
|
, которое задано на |
|||
множестве : |
:× |
; при этом мощность |
| | = |
. Изобразим это отношение в |
||
виде матрицы |
|
|
|
|
||
|
× |
|
|
|
|
|
Сколько всего различных n-арных отношений? Матрица размера |
|
, т.е. |
||||
матрица состоит из |
2 клеток, каждая из которых может принимать 2 |
различных |
||||
отношений. |
0 |
× |
|
|||
1 |
2 |
2 |
различных |
|||
варианта: либо |
, |
либо . Следовательно, всего существует |
|
|||
Теперь предположим, что отношение рефлексивное или иррефлексивное.
В этом случае главная диагональ фиксированная, т.е. могут меняться значения в |
|||
любых клетках, кроме главной диагонали. Здесь различных отношений будет |
2 |
− |
. |
Пусть отношение симметричное: |
2 |
|
|
Кононов Василий, Сагитова Адиля и Главатских Павел |
Глава 4 |
В этом случае различных отношений – 2 22+ .
|
Если отношение антисимметричное, то различных отношений – |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 3 22+ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Определение. |
|
Понятиезамыкания. |
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||
обладает некоторым свойством |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
называется |
|
Рассмотрим 2 |
|
отношения: |
|
1 |
и |
|
, которые определены на |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
и |
|
|
|
|
|
|
( 2) |
|
|
|
|
1 |
||||||||||
одном и том же множестве, т.е. |
|
|
|
2 |
|
|
|
|
|
22. При этом отношение |
|
|||||||||||||||||||||
тогда, когда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
– |
обозначим это как |
|
|
|
. Отношение |
|
|||||||||||||||
|
1 |
|
замыканием отношения |
|
|
относительно свойства |
|
|
тогда и только |
|||||||||||||||||||||||
1) |
обладает свойством , т.е. ( 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) |
1 |
является надмножеством 2: |
1 |
2. |
|
| |
= min 1( ) |
|
|
|
|
|
1( ) |
|
||||||||||||||||||
3) |
( ) |
. |
|
|
|
|
|
|
|
|
|
|
|1 1 |
|
|
|
|
|
||||||||||||||
|
и |
1 |
минимальное по |
мощности, т.е. |
|
|
|
|
|
|
|
|
|
|
|
для |
|
|
: |
|
и |
|||||||||||
|
Примеры1 2 замыканий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
Рефлексивное замыкание |
|
|
|
|
|
|
|
, где – единичное множество. Здесь на |
|||||||||||||||||||||||
|
каждой вершине есть |
рефлексивная петля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
( , ) |
|
( , ) |
|
||||||||||||||||
2) |
( , ) . Для каждой дуги |
= |
−1, |
|
т.е. |
|
|
и |
||||||||||||||||||||||||
Симметричное замыкание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
исходного отношения в замыкании строится
3)Транзитивное замыкание = 2 3 …, т.е. для всех цепей длины 2 итеративно строится транзитивная дуга:обратная дуга.

Классы отношений (продолжение). |
Глава 4 |
Кононов Василий, Сагитова Адиля и Главатских Павел |
1)Отношение эквивалентности – это отношение, которое является симметричным, рефлексивным и транзитивным одновременно.
||Отношение эквивалентности – это, по сути, отношение равенства 2-х объектов.
2) Отношение толерантности (похожести) – симметрично и рефлексивно.
Пример. Есть предметы круглые и квадратные, и есть предметы зелёные и красные. Если взять предметы: круглый зелёный и круглый красный, то они похожи по форме, но не похожи по цвету.
3) Отношение порядка (нестрого порядка) |
|
– антисимметрично и транзитивно. |
||||||||||||||||||
|
Отношение строгого порядка – иррефлексивное отношение порядка. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
Определение. Пусть – отношение эквивалентности на множестве |
|
||||||||||||||||||
|
|
|
|
элементов множества , |
|
|
|
|
|
|
|
|
||||||||
|
. Подмножество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
элементу , называется классом эквивалентности для |
и обозначается |
|
|
|||||||||||||||||
|
|
|
|
|
|
множества |
|
|
|
|
{ } |
|
|
|
|
|||||
|
Определение. |
Разбиение |
|
|
|
|
|
представление |
этого |
|||||||||||
|
|
[ ] |
= { | = –}. это |
|
||||||||||||||||
множества в виде попарно непересекающихся |
подмножеств |
|
|
: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
= и ∩ = (при ≠ ). |
|
|
|
|
|
||||||||||||
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема Кантора о разбиении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Всякое отношение |
эквивалентности |
|
на |
множестве |
|
|
задаёт разбиение |
||||||||||||
множества , причём, среди элементов разбиения нет |
|
пустых |
подмножеств. |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
Обратно, всякое |
разбиение множества , |
не содержащее пустых подмножеств, |
||||||||||||||||||
|
|
|
|
|
|
на множестве . |
|
|
|
|
|
|
|
|||||||
определяет отношение эквивалентности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
||Таким образом, нет такого класса эквивалентности, в котором нет вообще ни |
||||||||||||||||||||
||одного элемента (т.е. нет пустого подмножества). |
|
|
|
|
|
|
|
|
||||||||||||
Связь между разбиением множества на классы эквивалентности |
||||||||||||||||||||
и отношением эквивалентности, определённом на этом множестве |
||||||||||||||||||||
|
|
|
Всякое разбиение |
|
непустого множества |
|
определяет на |
|||||||||||||
|
Прямая теорема(.теорема Кантора о разбиении). |
|
|
|
|
|
|
|||||||||||||
этом множестве отношения эквивалентности |
|
|
такое, что: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 4 |
|||||||||||||||||||||||||||||||||||||
|
|
любые 2 элемента одного класса находятся в отношении |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
любые 2 элемента различных классов не находятся в отношении |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непустого множества |
|||||||||||
|
|
|
Доказательство. Пусть имеется некоторое разбиение |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
. Определим бинарное отношение |
|
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Т.е. 2 элемента |
|
и |
|
из |
|
( |
|
& ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
случае, |
если в |
|
|
|
|
|
|
множества |
|
связаны отношением |
в том и только в том |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
разбиении |
найдётся такой класс |
|
, |
которому одновременно |
||||||||||||||||||||||||||||||||||||||||
принадлежат элементы |
|
|
и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Определённое таким образом отношение |
и |
рефлексивно и симметрично. |
||||||||||||||||||||||||||||||||||||||||||||||||||
различные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
, 1 |
|
, 2 |
|
|
|
|
|
|||||||||||||||||||
Покажем транзитивность отношения |
|
. Пусть |
|
|
|
|
|
. Тогда по определению в |
|||||||||||||||||||||||||||||||||||||||||||||||
разбиении |
|
|
|
|
существуют классы |
|
|
и |
|
|
такие, |
|
что |
|
|
|
|
|
|
и |
|
|
|
. |
Т.к. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
= 2 |
|
|
|
|
|
|
, 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
классы в разбиении по определению не имеют общих элементов, то |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
, т.е. |
|
|
|
|
|
|
|
|
|
, |
|
|
поэтому |
|
|
|
|
|
, |
|
следовательно, |
|
|
– |
|
транзитивно. Таким |
|||||||||||||||||||||||||
образом, |
|
– отношение эквивалентности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Обратная |
теорема. Всякое отношение |
|
|
эквивалентности |
в непустом |
|||||||||||||||||||||||||||||||||||||||||||||||
множестве |
|
порождает разбиение этого множества на классы эквивалентности |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
такое, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
любые 2 элемента одного класса находятся в отношении |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
любые 2 элемента различных классов не находятся в отношении |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
отношение |
|
эквивалентности |
на |
||||||||||||||||||||||||
[ ] |
|
Доказательство. |
|
|
|
|
|
– |
|
некоторое |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элементу |
|
|
из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
множестве |
|
|
|
. Каждому |
|
|
|
|
|
: «подмножество |
|
|
|
|
– это все такие элементы , |
||||||||||||||||||||||||||||||||||||||||
//Запись |
|
|
|
[ ] |
= { |
| |
означает} |
, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
множества |
, состоящее из всех элементов |
|
находящихся в отношении |
|
|
с |
|||||||||||||||||||||||||||||||||||||||||||||||
//что |
|
|
[ ] = { | |
} |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
элементом |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
выполняется |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Система подмножеств |
[ ] образует разбиение множества . Действительно: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1) |
Каждое. |
|
подмножество |
[ ] |
≠ , |
|
т.к. в силу рефлексивности отношения |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
2) |
2 |
различных[ ] |
подмножества |
|
|
|
и |
|
|
не имеют общих элементов. Рассуждая |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
и |
[ ] |
в силу |
|
|
|
существование элемента |
|
|
|
[ ] |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
от противного, |
|
допустим |
|
|
[ ] |
|
|
[ ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
. Тогда |
|
|
|
|
|
и |
|
. Поэтому для любого элемента |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из [, ] |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
симметричности и транзитивности отношения вытекает |
|
|
|
|
, |
||||||||||||||||||||||||||||||||||||

Кононов Василий, Сагитова Адиля и Главатских Павел |
|
|
|
|
|
|
Глава 4 |
|||||||||
[ ] [ ] |
|
|
[ |
] = [ ] |
|
. |
Аналогично в другую |
сторону, |
||||||||
|
Следовательно, |
[ ] [, ] |
||||||||||||||
т.е. .[ ]Следовательно. |
, |
|
а это |
противоречит исходному |
||||||||||||
предположению об их неравенстве. |
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Объединение всех подмножеств |
|
|
совпадает с множеством |
, |
поскольку |
|||||||||||
для любого элемента |
|
выполняется условие |
. |
|
|
|
|
|||||||||
|
|
|
[ |
] |
|
|
|
образует разбиение[ ] |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
множества |
|
, |
|||||
Таким образом, система подмножеств |
[ ] |
|
||||||||||||||
удовлетворяющее условиям теоремы. |
|
|
|
|
|
|
|
|
|
|
||||||
