Глава 11. Равновесные состояния

термодинамических систем

11.1. Химический потенциал как

парциальное молярное свойство

Химическую реакцию можно рассматривать как процесс добавления в систему продуктов реакции и удаления из нее исходных веществ. Естественно, что при этом система предстает перед нами, как открытая по переносу масс веществ или числа их молей.

Как было показано (см. главу 10), состояние такой системы описывается с помощью характеристических функций, которые одновременно могут выступать в качестве термодинамических потенциалов, критериев направленности химических процессов, меры химического сродства, а также критериев равновесного состояния термодинамической системы.

Термодинамически равновесие определяется соотношением между концентрациями исходных веществ и продуктов реакции, при которых характеристическая функция, соответствующая условиям взаимодействия системы с окружающей средой, имеет минимальное значение.

Состав открытой системы может изменяться произвольно, при этом число характеризующих его переменных равно числу компонентов системы. Как было показано ранее, характеристические функции для открытой (а также закрытой) многокомпонентной системы являются функциями соответствующих переменных (энтропии, объема, давления, температуры, количества компонентов) в соответствии с ( … ).

U = U(S, V, n₁ … n_к)

Н = Н(S, -р, n₁ … n_к)

F = F(Т, V, n₁ … n_к)

G = G(Т, -р, n₁ … n_к).

Полные дифференциалы этих функций можно представить в виде:

.

Сравнение этих выражений показывает, что частные производные, стоящие под знаком суммы, равны между собой. Частная производная от любого термодинамического потенциала по числу молей данного компонента при постоянстве естественных параметров представляет собой не что иное, как химический потенциал _к компонента «к»:

.

Это соотношение уже приводилось (глава 10) как следствие из анализа поведения характеристических функций, обладающих экстенсивными свойствами.

Повторное обращение к этому соотношению вызвано тем обстоятельством, что для описания многокомпонентных систем требуется включение в рассмотрение парциальных молярных величин (ПМВ) экстенсивных свойств – см. раздел 3.3.

Из определения, приведенного в 3.3, следует, что любой экстенсивной функции соответствует парциальная мольная величина. В общем виде, согласно (3.24):

,

где Х – любое экстенсивное свойство.

Так, для одного из компонентов (1)

, (11.1)

а для второго (2)

, (11.2)

то есть парциальное мольное значение изобарно-изотермического потенциала (энергии Гиббса) равно химическому потенциалу этого компонента.

Следует, однако, помнить, что парциальные величины отличны от химических потенциалов, поскольку для химического потенциала производная берется при постоянных естественных переменных, а в случае парциальных величин – при постоянных температуре и давлении. Последнее следует из определения парциальной молярной величины (раздел 3.3), а также из соотношения (3.24).

Например, парциальная мольная величина внутренней энергии равна

,

но она не равна по определению химическому потенциалу. То же самое можно сказать об энтальпии () и энергии Гельмгольца ().

Из сопоставления (3.24), и (11.1), (11.2) следует, что только для изобарно-изотермического потенциала по определению

. (11.3)

Таким образом, при постоянных Т и Р химический потенциал – это парциальная мольная энергия Гиббса компонента системы данного состава с учетом происходящих в ней взаимодействий.

Функция G(n₁, …, n_i) обладает тем свойством, что при увеличении масс всех компонентов в одинаковое число раз энергия Гиббса системы увеличивается во столько же раз. Поэтому можно проинтегрировать

по общей массе при постоянстве температуры, давления и состава:

. (11.4)

При этом константа интегрирования равна нулю, поскольку, если все n_i=0, то энергия Гиббса также равна нулю. Из уравнения (11.4) видно, что энергию Гиббса можно представить как алгебраическую сумму произведений химических потенциалов компонентов на число их молей в системе.

В общем случае, как это следует из (11.3) и (11.4), химический потенциал показывает вклад одного моля компонента в изобарно-изотермический потенциал (энергию Гиббса) системы.

Таким образом, можно утверждать, что термодинамические свойства системы однозначно определяются, если известны зависимости химических потенциалов от состава, Т и Р.

Так как химический потенциал представляет собой парциальную молярную энергию Гиббса, то все термодинамические соотношения, в которые входит энергия Гиббса, справедливы и для химического потенциала. Так

; (11.5)

; (11.6)

; (11.7)

; (11.8)

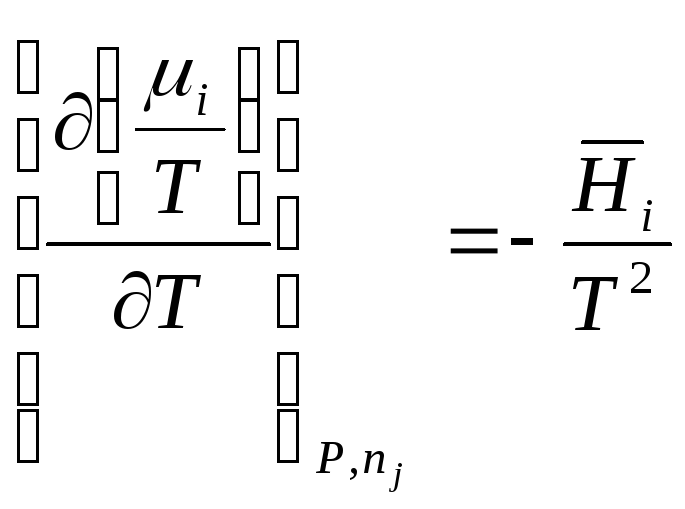. (11.9)

По аналогии с основными уравнениями для парциальных молярных величин (3.34) и (3.35) изменение химических потенциалов компонентов с изменением состава системы при постоянных температуре и давлении происходит в соответствии с уравнением:

(11.10)

и для одного моля системы:

. (11.11)

Уравнения (11.10) и (11.11) носят названия уравнений Гиббса-Дюгема; они были получены нами ранее (см. раздел 10.2) при анализе характеристической функции – энергии Гиббса. С помощью этих уравнений можно рассчитать значение химического потенциала одного из компонентов в многокомпонентной системе, если известны значения химических потенциалов других компонентов.

11.2. Методы определения парциальных молярных

величин (ПМВ)

С помощью ПМВ можно применять весь аппарат термодинамики к многокомпонентным системам (растворам) и к многофазным системам.

Рассмотрим двухкомпонентную систему при постоянных температуре и давлении. Пусть Х_общ. – любое экстенсивное свойство системы (U, Н, F, G, S, V). Для двухкомпонентной системы его можно записать в виде

Х_общ = Х_общ(Р, Т, n₁, n₂). (11.12)

При Р и Т = Const

. (11.13)

Запишем это уравнение через парциальные молярные величины

, (11.14)

где относится к растворителю, а- к растворенному веществу.

Проинтегрируем это уравнение при постоянстве состава

.

Const = 0, так как при n₁ и n₂ = 0, Х_общ = 0.

То есть

. (11.15)

Продифференцируем уравнение (11.15), полагая, что n₁, n₂, ,переменные величины:

. (11.16)

Сравнив уравнения (11.14) и (11.16), получим .

Разделим это уравнение на (n₁+n₂)

,. (11.17)

Разделив левую и правую часть уравнения (11.15) на (n₁+n₂), получим

, (11.18)

где Х – свойство одного моля раствора.

Для химического потенциала

N₁d₁+N₂d₂=0 (11.19)

=₁N₁+₂N_2. (11.20)

Для объема моля раствора

. (11.21)

Свойство одного моля раствора Х_ад называется аддитивным, если оно складывается из свойств ичистых компонентов пропорционально их содержанию в растворе, то есть

, (11.22)

где - свойство одного моля растворителя;

- свойство одного моля растворенного вещества.

Подставляя N₁=1-N₂, получим

. (11.23)

Из уравнений (11.22) и (11.23) видно, что зависимость Х_ад от N₂ линейная, так как коэффициенты ипостоянные величины, а в уравнении (11.18) зависимость Х от N₂ нелинейная, поскольку коэффициенты иизменяются от состава. Поэтому свойство раствора в общем случае представляет собой неаддитивную величину.

Отклонение свойства раствора от аддитивности называется изменением свойства раствора и записывается следующим образом:

, (11.24)

где Х – изменение свойства раствора,

- изменение парциального мольного свойства растворителя,

- изменение парциального мольного свойства растворенного вещества.

Существует два метода определения ПМВ – аналитический и графический.

Аналитический метод.

При вычислении аналитическим методом выражают зависимость свойства Х_общ от числа молей n₂ эмпирическим уравнением, например вида

. (11.25)

Парциальное мольное свойство определяют дифференцированием Х_общ по n₂

. (11.26)

Подставив в это уравнение величину n₂, можно определить для раствора данного состава. Например, необходимо определить парциальный мольный объем NаCl в водном растворе NаCl. Известно эмпирическое уравнение для общего объема

. (11.27)

Дифференцируем это уравнение по n_NaCl

. (11.28)

Подставив в это уравнение n_NaCl, находим парциальный мольный объем NаCl в водном растворе.

Графические методы.

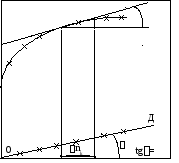
Эти методы расчета ПМВ более наглядны по сравнению с аналитическим методом. Один из них соответствует рассмотренному аналитическому методу. Зная значения изучаемого свойства для ряда растворов, содержащих одинаковые количества всех компонентов кроме одного компонента «к», и различные количества этого компонента, можно построить кривую Х_общ=f(n_к), наклон касательной в каждой точке которой (tg) дает производную и соответственно значение (рис. 11.1).

. (11.29)

Для однокомпонентной системы (чистого вещества «к») характерна линейная зависимость , выходящая из начала координат (прямая ОД на рис. 11.1.). Тангенс угла наклона tg определяет значение молярной величины . В многокомпонентной системе вследствие межмолекулярных взаимодействий между компонентами зависимость Х_общ=f(n_к) не является линейной (кривая АВС).

Парциальные молярные величины для обоих компонентов в бинарных системах можно определить также, построив графическую зависимость значения свойств для одного моля раствора (Х) от молярной доли одного из компонентов (например, N₂).

Заменим в уравнения Гиббса-Дюгема (11.17) и (11.18) N₁ через N₂ (N₁=1-N₂):

(11.30)

. (11.31)

Х_общ

Х_общ 

С

В

tg=

А

Рис. 11.1. Графическое определение парциальный молярных величин по зависимости экстенсивного свойства системы Х_общ от числа

молей компонента «к» (одно- и многокомпонентная система)

Продифференцируем уравнение (11.30):

. (11.32)

Совместив (11.32) с (11.31), получим

(11.33)

. (11.34)

Из уравнения (11.34)

. (11.35)

Уравнение (11.35) подставим в (11.30)

(11.36)

или . (11.37)

Отсюда . (11.38)

Если из уравнения (9.34) выразить

(11.39)

и подставить в (11.30), то получим

(11.40)

или . (11.41)

Полученные уравнения (11.38) и (11.41) лежат в основе построения графика Х=Х(N₂) – рис. 11.2.

С

Е

Н В  F

А 

D

О N₂ 1

Рис. 11.2. Графическое определение парциальных молярных величин по зависимости экстенсивного свойства Х от состава

системы (бинарная система)

Зависимость Х=Х(N₂) на рисунке иллюстрирует кривая АВС. Если к какой-либо точке этой кривой, например к точке В, провести касательную, то отрезки, отсекаемые ею на ординатах ОD (при N₂=0) и 1-Е (при N₂=1) будут соответственно равны значениям идля состава, отвечающего точке касания (метод пересечений). Это следует из рассмотрения треугольника ЕFВ:

ЕF=ВFtg; т.е.

или

.

Аналогичное можно доказать, рассмотрев треугольник DНВ.

11.3. Определение идеальных систем

При описании равновесных состояний системы, как и ранее, будем отталкиваться от поведения идеальных систем. В связи с этим, применительно к многокомпонентным системам, в которых происходит перераспределение масс в результате химических или фазовых превращений, следует уточнить понятия, связанные с определением идеальных систем.

Основой для определения идеальной многокомпонентной системы является уравнение типа (11.5), устанавливающее связь между изменениями парциальных молярных термодинамических величин компонента при образовании этой системы, т.е. при смешении компонентов:

. (11.42)

Это уравнение полностью определяет поведение каждого компонента многокомпонентной системы. По аналогии с идеальной смесью газов система считается идеальной, если для каждого компонента выполняются следующие условия:

-парциальная внутренняя энергия компонентов при их переходе в общую систему остается постоянной:

; (11.43)

-парциальный объем компонентов при их переходе в систему не изменяется

; (11.44)

и парциальные энтропии компонентов при их смешении возрастают на такую же величину, как и при образовании идеальной смеси газов. При этом изменение парциальной молярной энтропии должно следовать соотношению:

. (11.45)

Учитывая условия (11.43) и (11.45), из соотношения (11.42) получим для идеальной системы (смеси газов или раствора):

или , (11.46)

где - химический потенциал компонента в стандартном состоянии.

Соотношение (11.46) должно выполняться для всех компонентов идеальной системы. Это соотношение является также определением идеальной системы. К нему можно придти и по другому, используя в качестве исходного уравнения – (11.6). Очевидно, что результат, представленный уравнением (11.46), получается при дополнительном условии:

-парциальная энтальпия компонентов при их переходе в систему остается неизменной

. (11.47)

Различают два вида идеальных систем, что связано с выбором стандартного состояния для компонентов системы. Очевидно, что за стандартное состояние можно принять индивидуальное чистое вещество, так как в соответствии с (11.46) только при N_i=1 . Таким образом, с учетом (11.3), начальной точкой отсчета химического потенциала компонента системы является химический потенциал чистого вещества, или стандартная парциальная молярная энергия Гиббса компонента системы:

. (11.48)

Смесь, в которой для всех компонентов и при всех концентрациях (N_i) выполняется соотношение (11.46) при условии соответствия чистому веществу, называют совершенной идеальной системой.При этом уравнения (11.43)-(11.48) применимы к любой идеальной системе – газообразной, жидкой и твердой.

При рассмотрении идеальной смеси газов содержание газообразных компонентов смеси часто выражают с помощью парциальных давлений Р_i:

(11.49)

(закон Дальтона).

Подставляя в уравнение (11.46), получаем

, (11.50)

где - парциальное давление компонента в газовой смеси; Р⁰ – общее давление.

Для газов за стандартное состояние принимается идеальный газ, имеющий давление Р=1 атм (1,01310⁵ Па). Тогда уравнение (11.50) записывается в виде

. (11.51)

Отметим, что в физической химии часто встречаются выражения, включающие логарифм, казалось бы размерной величины. Однако, анализируя эти выражения, можно убедиться, как и в случаях (11.46) и (11.51), что на самом деле под логарифмом стоит отношение этой величины к некоторому стандартному значению (мольная доля N_i или относительное давление ).

Из уравнения (11.51) следует, что при =1,, что соответствует стандартному состоянию идеального газа, и мы снова приходим к выражению (11.48), т.е..

С учетом (11.48) уравнения (11.46) и (11.51) могут быть соответственно представлены в виде:

; (11.52)

, (11.53)

где - стандартная энергия Гиббса компонента «i».

Ко второму виду идеальных растворов принадлежат идеальные разбавленные – предельно разбавленные растворы. Их считают идеальными по отношению к растворителю: для них характерно идеальное смешение с растворителем. Это реальные растворы, в которых все компоненты, кроме одного (растворителя), присутствуют в очень малых количествах. Химические потенциалы всех компонентов в таких растворах также могут быть определены соотношением (11.46) при условии, что зависимость химического потенциала от логарифма концентрации линейная с тангенсом угла наклона, равным RT. В этом случае за стандартное состояние растворителя принимают чистое вещество. Если же агрегатные состояния растворителя и растворенного вещества не совпадают, то химические потенциалы последнего (микрокомпонента) выражают аналогичными уравнениями (11.46) с использованием моляльной «m» или молярной «С» концентрации вместо мольной доли. Соответственно химический потенциал отсчитывают относительно другого стандартного состояния, обозначаемого ^:

_i = ^_i(Т,Р) + RT ln m_i ; (11.54)

или

_i = ^_i(Т,Р) + RT ln С_i . (11.55)

Из этих соотношений следует, что ^_i является химическим потенциалом i-го компонента в стандартных состояниях, отвечающих одномоляльному или одномолярному раствору. Реальные растворы с такой достаточно большой концентрацией далеки по своим свойствам от идеальных систем. Поэтому говорят о гипотетическом растворе с единичной концентрацией и свойствами бесконечно разбавленного раствора (представляется, что в стандартном растворе, как и в бесконечно разбавленном, молекулы или ионы i-го компонента находятся далеко друг от друга и не взаимодействуют между собой).

Таким образом, если в системе все компоненты могут быть приняты равноценными, т.е. для всех компонентов за стандартное состояние выбрано чистое вещество, то в этом случае говорят о симметричном стандартном состоянии. Если же компоненты в системе неравноценны, то для растворителя, как правило, за стандартное состояние принимают чистое вещество, а для растворенных веществ – гипотетический раствор с единичной концентрацией, что отвечает несимметричному стандартному состоянию.

Так как в стандартных состояниях концентрации компонентов равны единице, то для стандартных изменений энергии Гиббса, энтропии и энтальпии можно записать соотношения:

(11.56)

(11.57)

. (11.58)

Таким образом, для расчета стандартной энергии Гиббса химического процесса получаем уравнение

, (11.59)

которое использовалось нами ранее (см. главу 10) для оценки направленности процесса.

Расчеты такого рода имеют прямое отношение к нахождению констант равновесия химических реакций, к исследованию влияния температуры и давления на химическое равновесие, а также встречаются при решении других задач.

11.4. Условия химического равновесия

Рассмотрим сначала общие принципы устойчивого равновесного состояния системы. Для любых систем при устойчивом равновесии должны выполняться следующие условия:

неизменность равновесного состояния системы при сохранении постоянства внешних условий;

подвижность равновесия, т.е. самопроизвольное его восстановление после прекращения внешнего возмущения;

динамический характер равновесия, т.е. установление и сохранение его, благодаря равенству скоростей прямого и обратного процессов;

возможность подхода к состоянию равновесия с двух противоположных сторон (прямого и обратного процессов);

минимальное значение любых термодинамических потенциалов и отсутствие их изменения.

Из общих условий выводятся конкретные для химических равновесий. Напомним дифференциальные уравнения для различных термодинамических функций

dU = ТdS – рdV +;

dН = ТdS + Vdр +;

dF = -SdТ – рdV +;

dG = -SdТ + Vdр +.

При равновесии – dU=0 (при постоянных S и V), т.е. в адиабатно-изохорическом процессе; dН=0 (при постоянных S и Р), т.е. в адиабатно-изобарическом процессе; dF=0 ( при постоянных Т и V), т.е. в изохорно-изотермическом процессе; dG=0 ( при постоянных Т и Р), т.е. в изобарно-изотермическом процессе.

Из анализа этих соотношений следует, что для любой термодинамической функции при постоянстве соответствующих естественных переменных условие химического равновесия предстает в виде:

=0,

Другим критерием равновесного состояния системы при протекании химических реакций является химическое сродство А^*. А^*=0 при достижении химического равновесия.

Запишем и сопоставим уравнения состояния многокомпонентной системы, в которой происходит перераспределение масс компонентов, через химические потенциалы _i и через химическое сродство А^* и химическую переменную , используя изменение энергии Гиббса:

dG = -SdТ + Vdр-А^*d

dG = -SdТ + Vdр +.

Сравнение этих уравнений приводит к соотношению

А^*d = -=(11.60)

или А^* = . (11.61)

Уравнение (11.61) выражает химическое сродство с помощью химических потенциалов.

Очевидно, что с помощью (11.61) можно выразить и условие химического равновесия. Так как при химическом равновесии А^*=0, то из (11.61) следует общее выражение условия химического равновесия:

. (11.62)

Таким образом, условие химического равновесия заключается в определенном соотношении химических потенциалов компонентов реакции. При этом в уравнении (11.61) химические потенциалы имеют текущие значения (в данный момент времени), а в уравнении (11.62) значения в условиях равновесия.

Одной из первых реакций, равновесие которой было изучено (Боденштейн, 1897), явилась реакция: Н_{2 +} I₂  2 НI.

При 721 К равновесие в этой реакции установилось за 80 мин при концентрации иодистого водорода, равной 0, 786 моль/л (рис. 11.3).

80 t, мин

Рис. 11.3. Динамическое равновесие реакции

Иллюстрацией приведенных выше характеристик устойчивого состояния системы применительно к реакции образования HI может служить механическая модель шарика, скатывающегося по наклонной поверхности (рис. 11.3.). Изобарный потенциал исходных веществ H₂ и I₂ характеризуется величиной G₁. По мере протекания реакции образования HI он уменьшается и достигает минимального значения G_min при концентрации иодистого водорода, равной 0.786 моль/л. При этой концентрации в реакции наступает состояние равновесия, G=0. К тому же равновесному состоянию можно подойти и с другой стороны. Разложение HI идет с уменьшением G₂ до того же минимального значения G_min . Равновесное состояние (как это следует из рис. 11.3.) наиболее устойчиво.

Выражением общих условий равновесия систем в приложении к химическим равновесиям является закон действующих масс, который удачнее других был сформулирован Гульдбергом и Вааге в 1867 г.: скорость гомогенной газовой реакции при постоянной температуре прямо пропорциональна концентрациям реагирующих веществ в степенях их стехиометрических коэффициентов.

Для реакции H₂ + I₂ 2HI V_пр. = K₁H₂I₂; V_обр. = K₂HI². В соответствии с динамическим характером равновесия можно записать, что V_пр. = V_обр.. Равновесие не зависит от направления процесса, поэтому прямое и обратное направление в каждом конкретном процессе выбираются условно:

K₁H₂I₂ = K₂HI², (11.63)

(концентрации можно выражать либо с помощью квадратных скобок, либо через С_инд., размерность концентрации моль/м³). Отношение констант скоростей прямой и обратной реакций К₁ и К₂ есть некоторая третья константа:

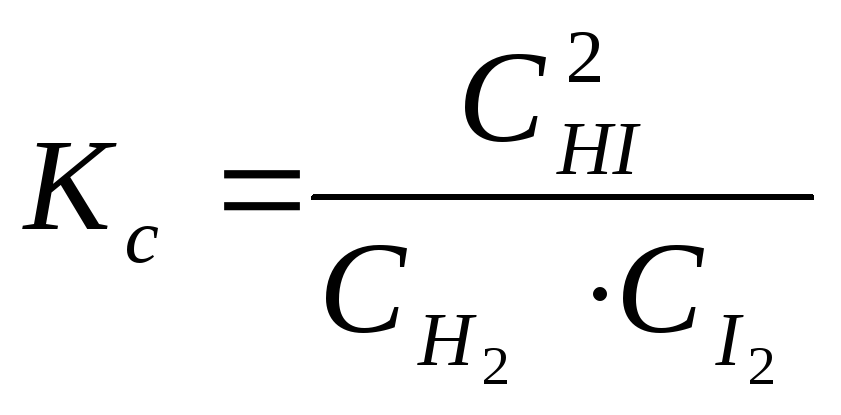или, (11.64)

или через парциальные давления:

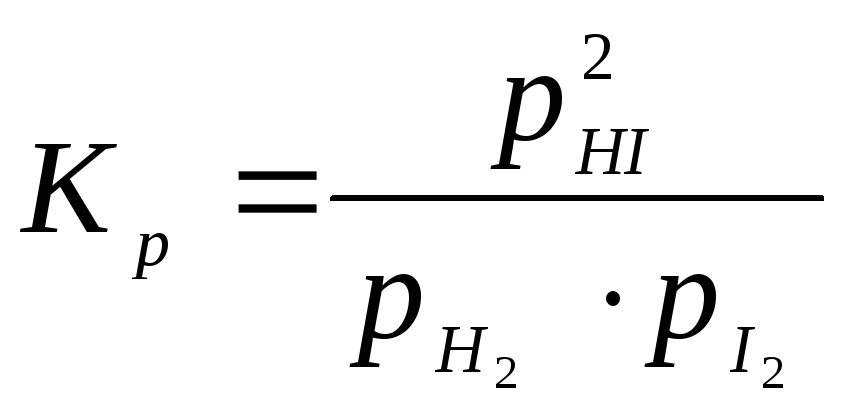. (11.65)

Для произвольной реакции: aA + bB = cC + dD, закон действующих масс в приложении к равновесным процессам может быть выражен в виде:

К_с = 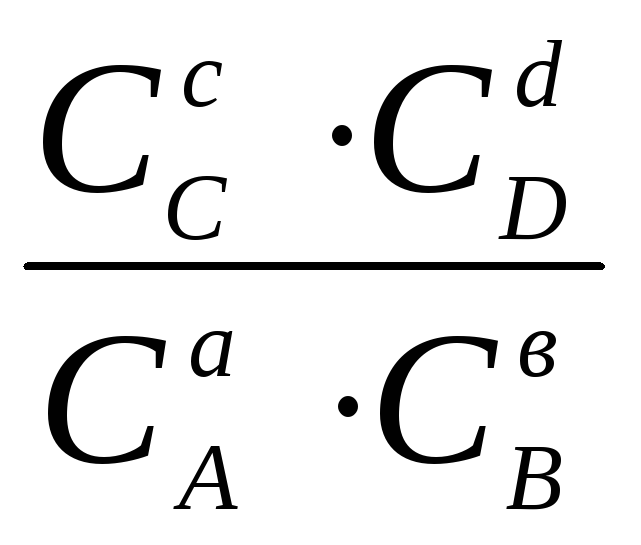или К_р = 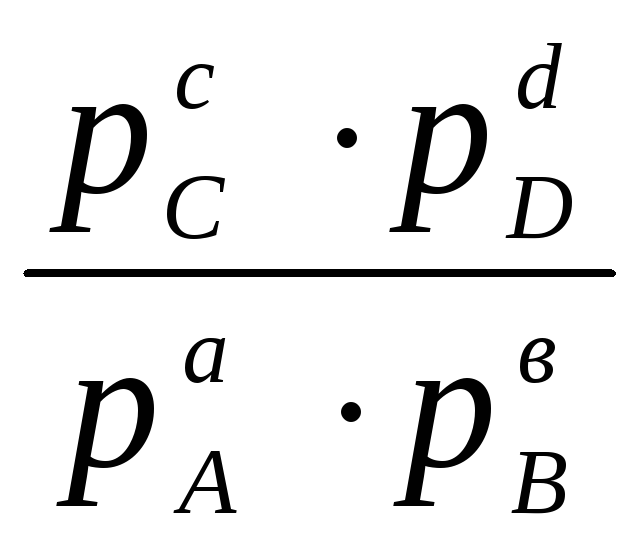(11.66)

Следовательно, состояние равновесия количественно может быть охарактеризовано определенной константой, выраженной либо через равновесные концентрации реагирующих веществ (К_с), либо через парциальные давления этих веществ в состоянии равновесия (К_р).

Соотношения (11.66) количественно выражают закон действующих масс, который гласит: при постоянных температуре и давлении константа химического равновесия (К_с или К_р) не зависит от состава системы, т.е. произведение равновесных концентраций (или равновесных парциальных давлений) компонентов реакции в степенях, равных стехиометрическим коэффициентам, не зависит от состава системы.

Для гомогенной газовой реакции связь между К_р и К_с основана на уравнении состояния идеального газа рV = nRT или р = сRT.

Отсюда

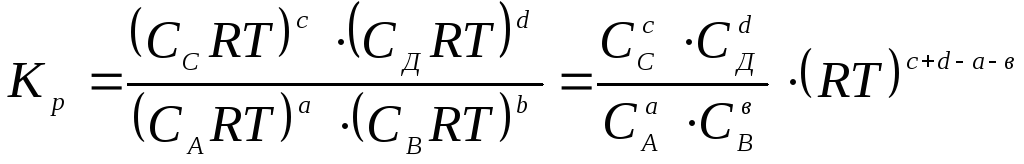, (11.67)

где с+d-а-в =  = _прод. - _исх.в.

К_р = К_с(RT) ^ ; при  = 0 К_р = К_с . (11.68)

Следует сказать о том, что константы К_р и К_с в (11.68) являются эмпирическими, поскольку здесь используются значения парциальных давлений и концентраций компонентов, определяемых на опыте. Следовательно, они имеют размерность: К_р = давление^ и К_с = молярность^ .

Однако, строго говоря, в уравнениях (11.66) необходимо пользоваться безразмерными величинами: N_i – мольная доля компонента или - относительное парциальное давление этого компонента. В этом случае:

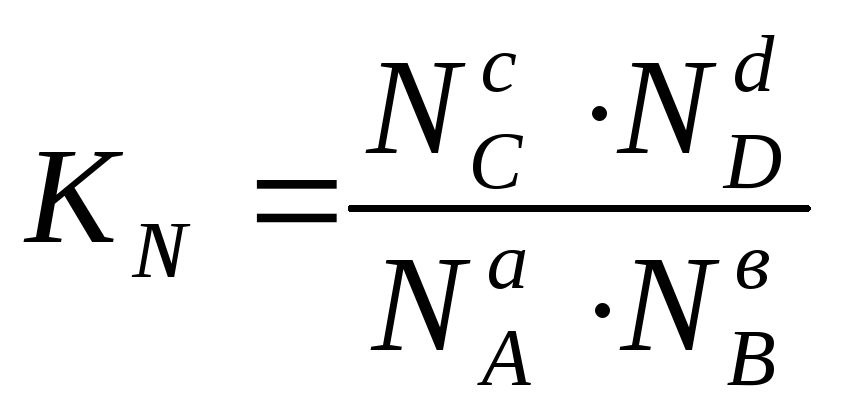К⁰ = и. (11.69)

К⁰ называется стандартной константой равновесия реакции. К⁰ и К_N – величины безразмерные.

Все четыре записи закона действующих масс (11.66) и (11.69) могут быть использованы при расчете состава равновесной смеси, но только одна из констант К⁰ вычисляется по соответствующим значениям G⁰, Н⁰ и S⁰.

В основе определения значений К_N, К_р, К_С фактически лежат соотношения

(11.70)

Справедливость приведенных соотношений (11.70) легко доказать, используя уравнения:

;;. (11.71)

Так как К⁰ не зависит от общего давления , то К_с и К_р, как это следует из (11.70), также не зависят от (для смеси идеальных газов). Отсюда, однако, не следует, что химический состав при равновесии не будет изменяться с давлением. Для выяснения влияния давления на состав равновесной смеси прологарифмируем уравнение K_N = K⁰()^-:

lnK_N = lnK⁰ –  ln. (11.72)

Найдем производную от полученного выражения по ln при постоянной Т:

(11.73)

Отсюда следует три вывода:

1) если 0, то K_N возрастает с повышением общего давления, т.е. химическое равновесие сместится в сторону продуктов реакции;

2) если 0, то K_N с ростом общего давления уменьшается и равновесие сместится в сторону исходных веществ;

3) если 0, то в этом случае на состав равновесной смеси изменение давления влияния не оказывает.

Напомним, что при выводе выражений для K_с и К_р (11.64) и (11.65) был использован кинетический подход (метод Гульдберга–Вааге) к состоянию равновесия обратимых химических реакций, в основе которого лежит равенство скоростей прямой и обратной реакции в момент равновесия. Этот подход достаточно продуктивен, но недостаточно строг, поскольку остается неясным, почему в выражениях для К_р и К_с все, что касается продуктов реакции, находится в числителе дроби, а не наоборот?

В этом смысле более строгим является термодинамический подход к выводу выражений закона действующих масс (11.66) и (11.69), предложенный Вант-Гоффом в 1885 г.

В состоянии равновесия

= 0 (11.74)

При постоянных Р и Т:

== 0 . (11.75)

С учетом стехиометрических коэффициентов (_i) в состоянии равновесия

= 0 (11.76)

Полученное уравнение аналогично выведенному ранее (11.62).

Для компонента гомогенной газовой реакции, подчиняющейся уравнению состояния идеального газа, в соответствии с (11.51)

и для реакции при равновесии:

()_прод - ()_исх.в. = 0 . (11.77)

Подставим в выражение (11.77) значение из уравнения (11.51):

[()+RT()]_прод – [()+RT()]_исх.=0

(11.78)

или [()_прод – ()_исх.в.]+

+[RT()_прод – RT()_исх.]=0. (11.79)

Заметим, что , тогда

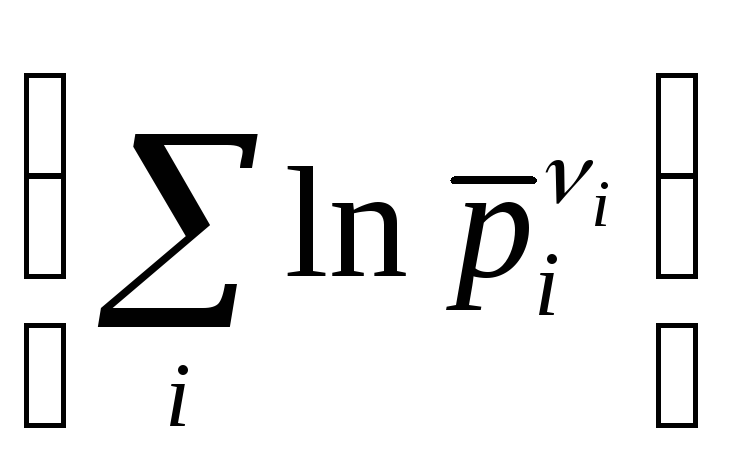_прод - _исх. = 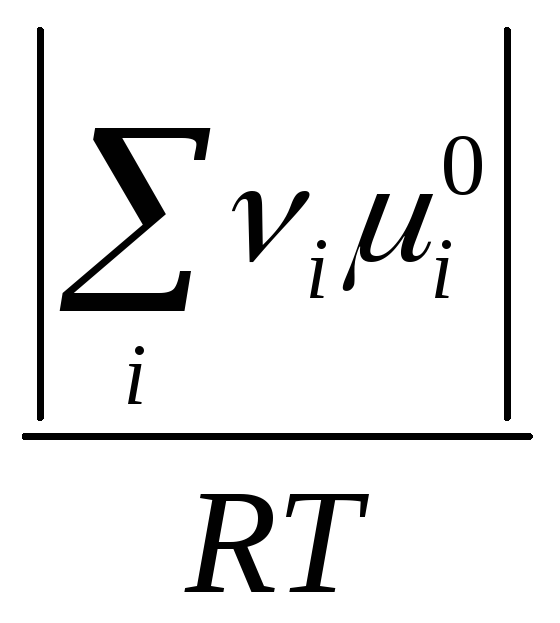= const. (11.80)

Исходя из этого, выражение для закона действующих масс: при постоянной температуре и общем давлении предстает в виде:

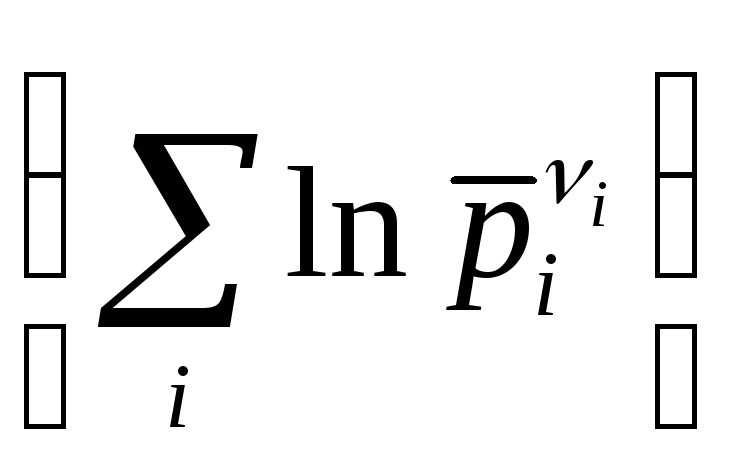_прод. – _исх. = const. (11.81)

Для произвольной реакции вида аА + вВ  сС + dD константу можно представить в форме ln К⁰, в этом случае для данной реакции закон действующих масс согласно уравнению (11.81) запишется так:

(ln+ ln) – (ln+ ln) = ln К⁰ (11.82)

или ln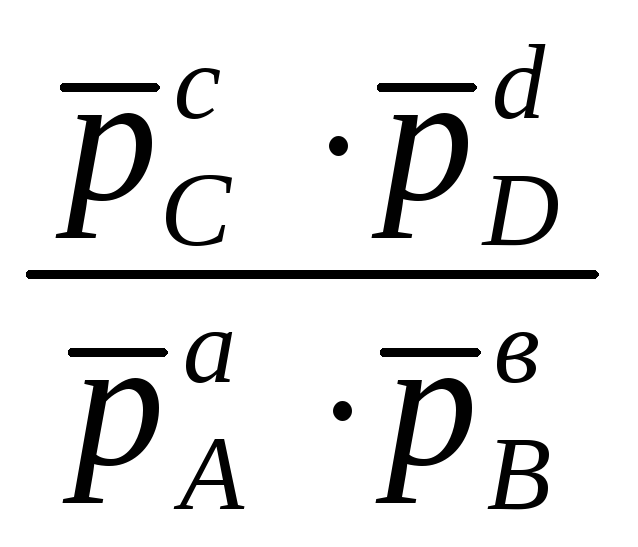= ln К⁰, т.е. = К⁰ . (11.83)

Имея в виду, что = N_i, нетрудно показать, что

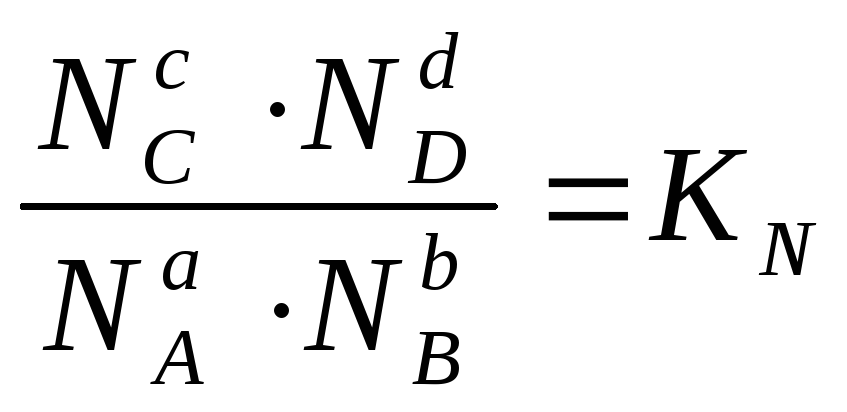, (11.84)

т.е. получены соотношения, приведенные выше в (11.69).

Эти соотношения могут быть представлены и в другом, более общем виде, выражающим закон действующих масс:

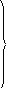
(11.85)

В условиях равновесия относительные парциальные давления (или моль­ные доли) всех компонентов связаны между собой. Нельзя изменить относи­тельное парциальное давление (или мольную долю) одного из них без того, чтобы не изменились остальные, причем численное значение соответствую­щих констант при данных условиях сохраняется тем же.

Для гетерогенных реакций в выражения для стандартной константы хи­мического равновесия К⁰ входят парциальные давления только газообраз­ных компонентов.

Например: С_гр + СO₂  2 СО.

Поскольку химический потенциал углерода (твердое вещество) является ве­личиной постоянной при постоянных р и Т, то

K⁰=.

Для реакции термической диссоциации карбоната магния

MgC0₃ = MgO + СO₂; К⁰ =.

Следует отметить, что величина К⁰, хотя и выражается через парциаль­ное давление газообразного компонента, зависит от свойств всех участни­ков реакции, поскольку соотношение (11.77) учитывает алгебраическую сумму химических потенциалов всех реагирующих веществ. Так, при термическом разложении MgCO₃ и СаСО₃ выражение для К⁰ одинаково, а численные значе­ния различны, т.к. химические потенциалы MgCO₃ и МgО отличаются от таковых для СаСО₃ и СаО.

11.5. Влияние изменения внешних условий на

химическое равновесия

В 1884 г. Ле-Шателье сформулировал принцип: если на систему, находя­щуюся в равновесии, воздействовать извне, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведенного воздействия, и равновесие сместится в том же направлении.

К смещению равновесия приводит нарушение равенства скоростей прямого и обратного процессов. В новом равновесном состоянии они опять одина­ковы, но не равны первоначальным.

На смещение равновесия химической реакции оказывают влияние изменение температуры, давления, концентрации реагирующих веществ.

1. Повышение концентрации продуктов реакции или исходных веществ в соответствии с законом действующих масс увеличит скорость обратной или прямой реакции.

Для повышения выхода продуктов реакции необходимо увеличивать концен­трацию исходных веществ и постоянно отводить продукты этой реакции, сни­жая их концентрацию в системе.

2. Давление оказывает влияние только на компоненты реакции, находящиеся в газовой фазе, при этом необходимо помнить следующее.

2.1. Моли любых газообразных веществ при одинаковых внешних усло­виях занимают равные объемы (закон Авогадро).

2.2. При повышении давления система стремится занять наименьший объем.

Теоретическое обоснование влияния общего давления на смещение хими­ческих равновесий приведено выше.

3. Повышение температуры стимулирует эндотермический процесс, т.е. при повышении температуры равновесие смещается в сторону реакции, иду­щей с поглощением тепла, для которой Н > 0.

Рассмотрим реакцию синтеза аммиака:

N₂ + 3H₂  2NH₃ + 92,4 (кДж)

1v 3v 2v   0

1. Влияние давления: повышение общего давления смещает равновесие вправо – в сторону веществ, занимающих меньший объем (2v).

2. Влияние температуры: реакция экзотермическая (Н < О), понижение температуры смещает равновесие вправо, т.е. для повышения выхода амми­ака температуру в системе необходимо понижать.

Все изложенное проиллюстрируем данными, приведенными в таблице.

Т а б л и ц а 11.?

Выход аммиака, %

Т, К	Давление, атм
	10	30	100
573 673 773 873	52 25,1 10,6 4,5	71 47 26,4 13,8	92 79,8 57,5 31,4

Выход аммиака максимален при наименьшей температуре и наибольшем давлении.

ПРИМЕРЫ

Задача 1. При смешении 1 моль уксусной кислоты и 1 моль этилового спирта протекает реакция (в I л объема)

CH₃COOH + C₂H₅OH  CH₃COOC₂H₅ + H₂O

При установлении равновесия в смеси оказалось 2/3 моль эфира. Рассчитать выход эфира, если:

1.1. в реакцию вступит 1 моль кислоты и 2 моль спирта;

1.2. в реакцию вступит по 1 моль кислоты, спирта и воды;

1.3. в реакцию вступят все компоненты по 1 моль.

Решение

Найдем константу равновесия приведенной реакции (К_с)

СH₃CООН + C₂H₅OH  CH₃COOC₂H₅ + Н₂0

 = 0 1 моль 1 моль 0 0

_равн. 1-2/3=1/3 1-2/3=1/3 2/3 моль 2/3 моль

K_c = = 4

1.1. СH₃CООН + C₂H₅OH  CH₃COOC₂H₅ + Н₂0

 = 0 1 моль 2 моль 0 0

_равн. 1-X 2-X X X

K_c = 4 = ; X₁ = 0,845 моль/л

X₂ = 3,05 моль/л (не имеет физического смысла)

Ответ: состав равновесной смеси: кислоты - 0,155 моль/л, спирта -1,155 моль/л, эфира и воды - по 0,845 моль/л.

1.2. СH₃CООН + C₂H₅OH  CH₃COOC₂H₅ + Н₂0

 = 0 1 моль 1 моль 0 1 моль

_равн. 1-X 1-X X 1+X

K_c = = 4; X₁ = 0,543 моль/л

X₂ = 2,46 моль/л (не имеет физического смысла)

Ответ: состав равновесной смеси: кислоты и спирта по 0,457 моль/л, эфира - 0,543 моль/л и воды - 1,543 моль/л.

1.3. СH₃CООН + C₂H₅OH  CH₃COOC₂H₅ + Н₂0

 = 0 1 моль 1 моль 1 моль 1 моль

_равн. 1-X 1-X 1+X 1+X

K_c = = 4; X₁ = 0,333 моль/л; X₂ = 3,0 моль/л (не имеет физического смысла)

Ответ: состав равновесной смеси: кислоты и спирта - по 0,667 моль/л, эфира и воды - по 1,333 моль/л.

Проведем анализ полученных результатов.