MathAn / !Лекция_II(4)-№5(2014-15)_St

Математический анализ. Модуль-4 (2014-15)

Лекция №5 Тригонометрический ряд. Ряды Фурье

1. Тригонометрический ряд и его свойства

В степенных рядах используются простейшие степенные функции

1, x, x2 , , xn , .

? … ? …

Def 1. Тригонометрическим рядом называется ф.р.

a20 a1 cos x b1 sin x a2 cos2x b2 sin 2x an cosnx bn sin nx , (2)

где a0 , a1, a2 ,b2 , , an ,bn - коэффициенты тригонометрического ряда.

Важные свойства

1.Периодичность функций системы (1) и суммы тригонометрического ряда.

2.Ортогональность функций системы (1).

S1. ! Все члены ряда - периодические функции с общим периодом T 2 .

Если все члены ряда

! Если ряд сходится на , , то он сходится на всей числовой прямой и его сумма является периодической функцией с периодом 2 .

1

Математический анализ. Модуль-4 (2014-15)

! Тригонометрические ряды можно использовать в качестве моделей при

изучении периодических процессов в различных предметных областях, в том числе и экономике.

S2. Ортогональность системы функций (1) на , интеграл по отрезку, от произведения любых двух различных функций системы (1) равен 0, а

интеграл по отрезку , от квадрата любой функции системы (1) отличен от 0.

sin kx cosnx dx 0 . (S2.4)

2

Математический анализ. Модуль-4 (2014-15)

Теорема 0

тригонометрическому ряду ряд (*) - абсолютно сходящийся (см. признак Вейерштрасса). #

2. Ряд Фурье

Теорема 1

Если функция f x определена и интегрируема на , , разлагается в тригонометрический ряд (3)

который можно почленно интегрировать, то это разложение единственно.

Доказательство

Интегрируя ряд (3), получим

получим

3

Математический анализ. Модуль-4 (2014-15)

f x sin kx dx bk

Фурье (р.Ф.).

4

Математический анализ. Модуль-4 (2014-15)

Def 2. Функция f x называется удовлетворяющей условиям Дирихле на a, b , если она

непрерывна на a, b или имеет конечное число точек разрыва I-го рода;

кусочно-монотонная на a, b , т.е. отрезок a, b можно разделить на конечное число отрезков, внутри которых функция f x либо только возрастает, либо только убывает, либо постоянна.

Пусть периодическая функция f x удовлетворяет условиям Дирихле на любом

отрезке из R, тогда по формулам (Ф.1-Ф.3) можно найти коэффициенты Фурье и построить ряд Фурье.

Теорема 2 (Дирихле)

Если периодическая функция f x с периодом 2 удовлетворяет на любом отрезке из R условиям Дирихле, то р.Ф. для функции f x сходится x R . При этом в каждой точке непрерывности функции f x сумма ряда

S x f x , а в каждой точке разрыва x сумма S f 0 f 0 . 2

Пример 1

f x x, x определена как периодическая функция с периодом 2 . Разложить f x в р.Ф.

Решение

f x удовлетворяет условиям Дирихле (рис.1)

Рис.1

…

5

Математический анализ. Модуль-4 (2014-15)

3. Ряд Фурье для четных и нечетных функций

Напоминание

произведение двух четных и двух нечетных функций – четная функция;

произведение четной и нечетной функции – нечетная функция.

Теорема 3

g x : x , и g x g x (нечетная функция), тогда

коэффициенты Фурье:

6

Математический анализ. Модуль-4 (2014-15)

Вывод

Если функция f x - четная, то ряд Фурье содержит только косинусы;

если f x - нечетная, то только синусы.

Пример 2

f x x , x определена как периодическая функция с периодом 2 . Разложить f x в р.Ф.

Решение

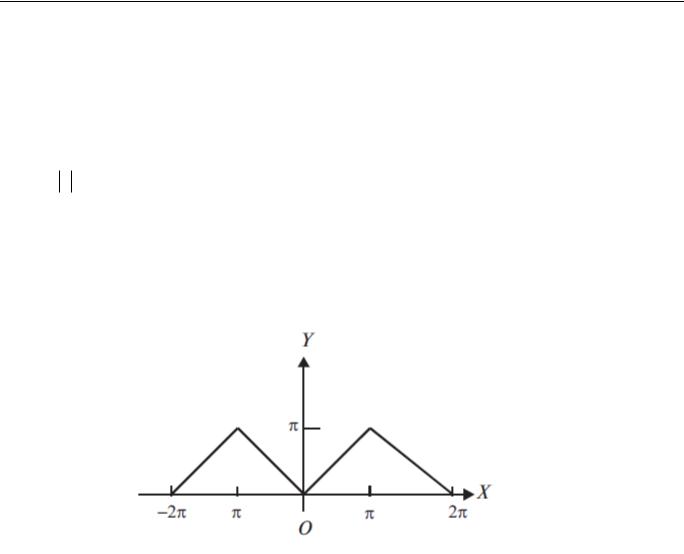
f x - четная и удовлетворяет условиям Дирихле (рис.2)

Рис.2

…

7