ОИТОУ / lab4 / Частот_хар

Цель работы: Освоить метод идентификации объекта по его частотным характеристикам.

Получение модели по частотным характеристикам

Моделирование с помощью активного эксперимента выполняется обычно вне контура регулирования. Наиболее распространены активные воздействия в виде синусоидальных сигналов, а также в виде ступенчатых и импульсных воздействий.

Пусть на частотах _i, i=1..N выполняется снятие частотных характеристик.

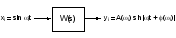
Рис. 1. Схема снятия частотных характеристик

По 2N результатам эксперимента

A(_i) = A_i; (_i) = _i

вычислим значения вещественной и мнимой частотных характеристик

R_i =A_i cos _i; Ii = Ai sin _i.

Будем искать передаточную функцию в виде

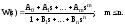
Соответствующее описание системы в виде дифференциального уравнения:

Пусть для краткости положим n = 3 и m = 2, тогда для каждого i-го опыта

y = A_i sin(_it + _i); x = sin _it;

dy/dt = _i A_i cos(_it + _i); dx/dt = _i cos _it;

d²y/dt² = _i² A_i sin(_it + _i); d²x/dt² = _i² sin _it;

d³y/dt³ = _i³ A_i cos(_it + _i).

После подстановки этих выражений для установившегося синусоидального режима в дифференциальное уравнение получим тождество, справедливое на данной частоте _i для любого момента времени t:

A_i sin(_it + _i) + B₁ _i A_i cos(_it + _i)  B₂ _i² A_i sin(_it + _i) 

 B₃ _i³ A_i cos(_it + _i) = A₀ sin _it + A₁ _i cos _it  A₂ _i² sin _it

Учтем преобразования:

A_i sin(_it + _i) = A_i (sin _it cos _i + cos _it sin _i) = R_i sin _it + I_i cos _it

A_i cos(_it + _i) = A_i (cos _it cos _i  sin _it sin _i) = R_i cos _it  I_i sin _it

Поскольку тождество имеет место для любого момента времени t, то выберем некоторый момент t^* из условия:

_it^* = /4, т.е. t^* = /(4_i),

тогда sin _it^* = cos _it^* и тождество можно записать как

R_i + I_i + B₁ _i (R_i  I_i)  B₂ _i² (R_i + I_i)  B₃ _i³ (R_i  I_i) = A₀ + A₁ _i  A₂,

или, собирая неизвестные в левой части:

A₀ + A₁ _i  A₂  B₁ _i (R_i  I_i) + B₂ _i² (R_i + I_i) + B₃ _i³ (R_i  I_i) = R_i + I_i.

Если в полученную систему уравнений подставить экспериментальные значения R_i и I_i, то равенство для каждого i будет приближенным. Тогда систему уравнений можно решать МНК, введя невязку как разность между левой и правой частями. Введенная таким образом невязка будет линейна относительно искомых коэффициентов и вычисление их МНК даст несмещенные оценки.

Точность вполне удовлетворительная (различие в коэффициентах обусловлено лишь погрешностями округления).

Метод наименьших квадратов в многомерном случае

Будем рассматривать здесь многомерную модель как модель со многими входами и одним выходом:

Рис. 2. Многомерная система

Сигналы на входах и выходах считаем центрированными, т.е.

M[x_j(t)] = 0, j = 1, 2, ..., k; M[y(t)] = 0.

Модель ищем в виде линейной комбинации входных сигналов

Помеху считаем аддитивной

Выбираем N >> k моментов времени t_i, i = 1, 2, ..., N и в каждый из этих моментов наблюдаем все входы и выход.

Интервал между t_i не играет роли. Важно только, что в момент взятия отсчетов система должна быть в установившемся состоянии, т.е. интервал должен быть достаточным для практического окончания переходных процессов при изменении очередного состояния системы.

Введем обозначения:

x_j(t_i) = x_ij; y(t_i) = y_i; (t_i) = _i.

тогда

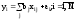
В матричной форме

Y = XB + E,

где

Откуда получаем т.н. нормальные уравнения МНК:

X^TXB = X^TY.

Решение нормальных уравнений

B = (X^TX)^-1 X^TY

Порядок выполнения лабораторной работы.

1. С помощью метода частотных характеристик определить параметры модели вида

,

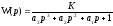2. Проверить работу метода в тех случаях, когда порядок модели больше/меньше порядка объекта.

3. Сделать выводы.

Содержание отчета.

1. Цель работы.

2. Передаточная функция объекта.

3. Переходные и частотные характеристики объекта.

4. Основные расчетные соотношения.

5. Найденная модель.

6. Модели для случаев, когда порядок модели больше/меньше порядка объекта.

7. Выводы.