
Высшая математика ч2 (3.сем)
.pdf
6. Найти циркуляцию векторного поля |
|
|
|
|
вдоль |
|
F |
yi |
zj |
xk |
|||
замкнутого |
контура, полученного от |
пересечения |
сферы |
|||
x2 y2 z2 |
R2 координатными плоскостями, расположенными в |
|||||
первом октанте.
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 19 |
|
|
|
|
|
У |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1. |
Построить область, площадь которой выражается интегралом |
|||||||||||||||||||||||
1 |
|
1 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
dx |
|
dy . |
Вычислить |
|
|
|
этот |
|
|
интеграл. |
|
Поменять |
порядок |
||||||||||||
0 |
1 1 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
Т |
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегрирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2. |
Определить массу |
|
|
|
тела, |
|
|
ограниченного |
поверхностями |
|||||||||||||||
x2 |
|
y2 |
z2 |
0; z |
h , |
|
если |
|
|
|
|
|
й |
в |
каждой |
точке |
|||||||||
|
|
|
|
|
|
|
|
1 |
|
cos x |
|
|
точки |
|
|
|
|
|
|
||||||
пропорциональна аппликате этой |
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
||||
|
3. |
Вычислить |
|
|
cos2 xdl |
, |
|
где |
L |
– |
дуга |
кривой |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
полным дифференц аломнекоорой функции. Найти эту функцию. |
|||||||||||||||||||||||||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
sin x 0 |
x |
|
. |
т |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4. |
Доказать, |
|
что |
|
выражение |
3x2e ydx |
|
x3e y |
1 dy |
является |
||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
з |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5. |
Вычислить |
|
x |
|
|
z |
|
|
dydz, |
где |
S |
– внешняя |
сторона |
|||||||||||
|
|
|
о |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхн сти |
x |
|
9 |
y2 , отсеченной плоскостями z |
0; z |
2 . |
|||||||||||||||||||
|
6. |
п |
|
|
|
, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Найти rot r |
, a |
r |
|
r |
|
xi |
2yj zk |
,a |
2i |
j |
k . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 20 |
|
|
|
|
|
|
||||||
е1. С помощью двойного интеграла вычислить площадь фигуры, |
|||||||||||||||||||||||||
ограниченной линиями |
|
|
|
a 1 |
cos |
|
; |
a cos . |
|
|
|
||||||||||||||
Р2. Определить массу сферического слоя между поверхностями |
|||||||||||||||||||||||||
x2 |
|
y2 |
z2 |
a2; x2 |
y2 |
|
|
z2 |
|
4a2 , если плотность в каждой точке |
|||||||||||||||
обратно пропорциональна расстоянию точки от начала координат.
80

3. |
Вычислить |
|
|
|
ydl , где L – дуга параболы |
y2 |
2x , отсеченная |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параболой x2 |
|
|
2y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4. |
Показать, |
|
|
|
что |
|
ydx |
x |
|
y dy |
|
по |
любому |
замкнутому |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
контуру равен нулю. Проверить, вычислив интеграл по контуру |
||||||||||||||||||||||||||||||
фигуры, ограниченной линиями y |
|
|
x2, y |
|
4 . |
|
|
|
|
|
||||||||||||||||||||
5. |
Вычислить |
|
|
|
|
массу |
поверхности |
|
z |
x , |
ограниченной |
|||||||||||||||||||
плоскостями |
|
x |
|
|
y |
1; y |
0; x |
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||
|
|
|
|
если поверхностная плотность в |
||||||||||||||||||||||||||
каждой точке равна абсциссе этой точки. |
|
|
|
|
|
|
Т |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
6. |
Найти циркуляцию вектора |
|
|
y |
по замкнутой кривой, |
|||||||||||||||||||||||||
|
F |
|
i |
|||||||||||||||||||||||||||
составленной из верхней половины эллипса |
x |
Н4cost; y sin t и |
||||||||||||||||||||||||||||
отрезка оси Ox . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вар ант 21 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
||||
1. |
С помощью двойного интег ала выч слить площадь фигуры, |
|||||||||||||||||||||||||||||
ограниченной линиями xy |
a2; y |
и |
|
a |
0 . |
|
|
|
||||||||||||||||||||||
|
x; y |
|
2a |
|
|
|
||||||||||||||||||||||||
2. |
Определить |
|
|
|
массу |
|
р |
|
2 |
|
y2 |
|
z2 |
|
a2; z 0 , если |
|||||||||||||||
|
|
|
п лушара x |
|
|
|
||||||||||||||||||||||||
плотность его в каждой |
очкеравна аппликате этой точки. |
|||||||||||||||||||||||||||||
3. |
Вычислить |
|
|
|
|
|
т3 |
где |
|
L |
– |
|
дуга |
кривой y |
lnsin x от |
|||||||||||||||
|
|
|
sin |
xdl |
, |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
до |
x |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
4 |
|
2 |
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
Вычислитьо e2x |
y2 |
dx 1 |
2xy dy , |
где |
C |
– |
треугольник |
||||||||||||||||||||||
|
п |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
2; x |
|
0; y |
x . |
Доказать, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||
сторонами которого являются прямые |
|
|||||||||||||||||||||||||||||
чтоеданный интеграл по любому замкнутому контуру равен нулю. |
||||||||||||||||||||||||||||||
5. |
Найти площадь части поверхности |
y |
|
x2 |
z2 , |
вырезанной |
||||||||||||||||||||||||
Р |
|
|
|
2 |
|
x |
2 |
|
1 и расположенной в первом октанте. |
|||||||||||||||||||||
цилиндром z |
|
|
|
|
|
|
||||||||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти div u,v |
, где u |
|
2xi |
|
yj |
|
3zk |
;v |
3yi |
zj |
xk . |
|||||||||||||||||||
81 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
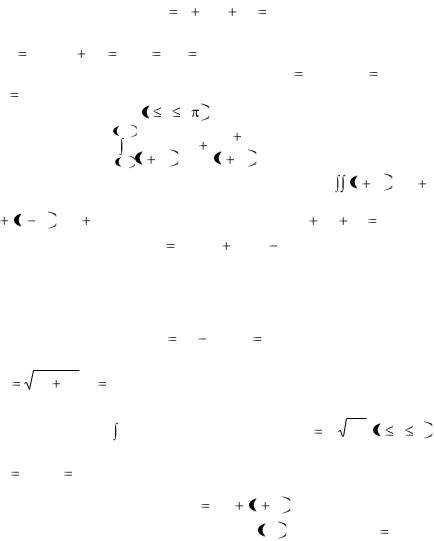
Вариант 22
1. С помощью двойного интеграла вычислить площадь фигуры,
ограниченной линиями y2 |
|
|
4 x; x 3y 0 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2. |
|
Определить |
объем |
|
тела, |
ограниченного |
поверхностями |
|||||||||||||||||||||||||||
z2 |
|
|
2ax; x2 |
y2 |
|
ax; z 0; y 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
3. |
|
Найти |
массу |
дуги |
винтовой |
линии |
x |
4a cost, y |
|
4a sin t, |
||||||||||||||||||||||||
z 3at , |
если плотность |
ее |
|
в |
|
|
каждой |
точке |
пропорциональна |
||||||||||||||||||||||||||
аппликате этой точки |
0 |
t |
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Т |
|
||||||||||||||||||||||||
|
4. |
|
Вычислить |
3,2 |
|
x |
|
|
|
|
|
|
|
|
|
2x |
y |
dy . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1,1 |
|
x |
y |
|
|
|
|
|
|
|
x |
y |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y dydz |
|||||||
|
|
Используя формулу Остроградского, вычислить |
x |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
y |
|
|
x dxdz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
z2 |
|
1. |
|
|
||||||
|
|
|
zdxdy через поверхность шара x2 |
y2 |
|
|
|
||||||||||||||||||||||||||||
|
6. |
|
|
|
|
|
|
|
|
|
|
3x |
2 |
y |
2 |
|
|
3 |
2 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
Найти rotF |
, если F |
|
|
|
i |
2yйzj z x |
k . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ва иант 23 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1. |
|
С помощью двойн |
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
интеграла вычислить площадь фигуры, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ограниченной л н |
|
|
|
го |
|
|
|
|
x . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
ay |
|
|
x |
|
|
|
2ax; y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2. |
|
Вычислить |
|
|
|
т |
|
|
|
|
|
ограниченного |
поверхностями |
|||||||||||||||||||||
|
|
|
массу |
|
тела, |
|
|
||||||||||||||||||||||||||||
y |
|
|
|
x2 |
z2 ; y |
b |
, |
|
если |
|
|
|
плотность |
в |
каждой |
его |
точке |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
ями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
пропорци нальназрдинате этой точки. |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
3. |
|
Вычислить |
|
xyzdl , где L – дуга кривой |
z |
8t3 |
|
0 |
t 1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
п |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
t |
2 |
; y t; . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4. |
|
Найти |
работу |
силы |
|
|
|
|
|
|
|
|
|
при |
перемещении |
|||||||||||||||||||
|
|
|
|
F |
|
|
|
xyi |
|
x |
y |
j |
|||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по параболе |
y |
x |
2 |
. |
|||||
массы m из начала координат в точку A 1, 1 |
|
||||||||||||||||||||||||||||||||||
82

5. |
С помощью формулы Стокса показать, что |
yzdx |
|
xzdy |
xydz |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
по любому замкнутому контуру равен нулю. Проверить, вычислив |
|||||||||||||||||||||||||||
интеграл |
по |
контуру |
треугольника |
|
с |
вершинами |
O 0, 0, 0 ; |
||||||||||||||||||||
A 1,1, 0 ; B 1,1,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6. |
Вычислить |
|
|
поток |
вектора |
|
|
|
|
|
|
через |
|||||||||||||||
|
|
|
|
a |
x3i |
y3 j |
|
zk |
|
|
|||||||||||||||||
поверхность шара x2 |
|
y2 |
|
z2 a2 . |
|
|
|
|
|
|
|
|
|
Т |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Вариант 24 |
|
|
|
|
Н |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|||||||||
1. |
Вычислить площадь фигуры, ограниченной линиями |
|
y |
|
ln x; |
||||||||||||||||||||||
x y |
1; x 3. |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4a2 |
|
|||||||
Вычислить объем тела, ограниченного поверхностями y2 |
|
3ax; |
|||||||||||||||||||||||||
y2 |
ax; z |
h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Найти массу дуги полуокружности x |
|
a cost; y |
|
a sin t , |
если |
|||||||||||||||||||||
плотность ее в каждой точке |
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
авна |
x |
2 y . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4. |
Найти |
работу, |
|
|
о |
и |
|
|
4x |
2 |
|
|
|
|
при |
||||||||||||
|
пр изв димую |
|
силой |
F |
|
i |
xyj |
|
|||||||||||||||||||
перемещении массы |
|
т |
|
|
|
|
|
x3 |
от точки O 0, 0 |
|
до точки |
||||||||||||||||
m |
вд ль дуги |
y |
|
|
|||||||||||||||||||||||
C 1, 1 . |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
Вычислить |
|
|
x2dydz |
y2dxdz |
zdxdy , |
где |
S |
|
– |
|
внешняя |
|||||||||||||||
|
|
что |
S |
|
|
|
|
|
2 |
|
2 |
|
|
2 32 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сторона части сферы, расположенной в первом октанте. |
|
|
|
|
|
||||||||||||||||||||||
|
п |
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6. |
Д казать, |
|
поле |
|
|
xi |
|
yj |
|
zk |
|
|
является потенциальным. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
е |
|
|
|
|
|
|
|
|
x |
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
Вариант 25 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Вычислить площадь фигуры, ограниченной линиями |
y |
x; |
||||||||||||||||||||||||
x2 |
y2 |
2x; y |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
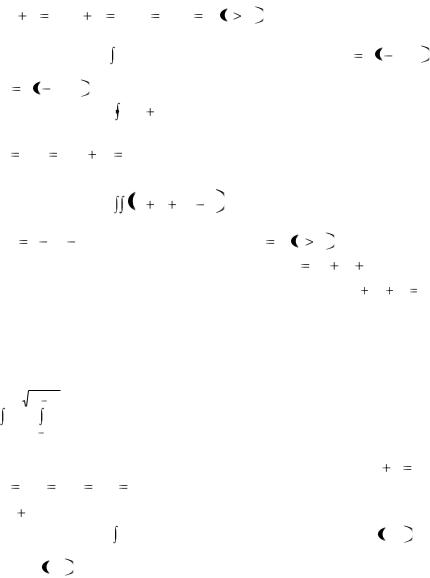
2. Определить массу тела, ограниченного поверхностями
2x |
|
|
z 2a; x y |
|
a; y2 |
ax; y |
0 |
y |
0 , |
если плотность в каждой |
||||||||||||||
его точке равна ординате этой точки. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
3. |
Вычислить |
|
ydl , где L – первая арка циклоиды x |
3 t |
sin t ; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
y |
|
3 1 |
cost . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4. |
Вычислить |
|
xdy |
ydx , где |
C |
– треугольник со сторонами |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
Т |
|
|||
|
|
0; y |
|
0; |
x |
|
y |
|
1. Доказать, |
|
|
|
|
|
Н |
|
|
|||||||
x |
|
|
a |
|
b |
|
что данный интеграл по любому |
|||||||||||||||||
замкнутому контуру равен нулю. |
|
|
|
|
Б |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
5. |
Вычислить |
|
x2 |
y |
z2 |
4 dS , |
где |
S |
– |
часть поверхности |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
9 |
x2 |
z2 , отсеченная плоскостью y |
0 |
y |
0 . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
6. |
Найти циркуляцию векторного поля |
F |
yi |
zj |
xk |
вдоль |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
|
|
y2 |
z2 |
|
||
замкнутого контура, полученного от пересеченияйсферы x2 |
4 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
||
координатными плоскостями, асположенными в первом октанте. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
26 |
|
|
|
|
|
|
|
|||
|
1. |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Построить облас ь, площадь которой выражается интегралом |
|||||||||||||||||||||||
a |
|
|
a2 |
y |
2 |
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
о |
|
|
|
|
этот |
|
интеграл. |
Поменять |
порядок |
||||||||||
dy |
|
|
dx . |
|
|
Вычислить |
|
|
||||||||||||||||
0 |
|
|
a |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
интегрир вания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a; |
||||
|
2. |
Вычислить массу тела, ограниченного поверхностями x |
z |
|||||||||||||||||||||
x |
|
0; y |
|
0; y |
|
a; z |
0 , если плотность его в каждой точке равна |
|||||||||||||||||
Р |
|
y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. |
Вычислить |
|
xdl , где |
L – отрезок прямой от точки 0, 0 |
до |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки 1, 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
84

4. |
|
|
|
|
|
|
|
|
|
|
|
при перемещении |
||||
Вычислить работу силы F |
y |
i |
|
y |
x |
j |
||||||||||
единицы массы по дуге параболы y |
|
a |
|
|
x |
2 |
|
из точки A |
a; 0 к |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
a |
||||||||||||||
точке B 0,a . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||
5. |
Вычислить |
x2dydz |
y2dxdz |
z2dxdy , |
где S |
– |
||||||||||
внешняя |
||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
|
|
|
|
R2 |
|
|
|
|
||||||
сторона поверхности конуса z2 |
y2 |
|
|
|
x2; 0 |
x |
3 . |
|
||||||||
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Н |
|
||||||
6. |
Найти линейный интеграл вектора |
|
|
|
вдоль первой |
|||||||||||
a |
x3i |
y3 j |
||||||||||||||
четверти окружности x 3cost; y |
3sin t . |
Б |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
Вариант 27 |
|
|
|
|
|
|
|
|
|
||||
1. |
|
|
|
|
|
й |
|
|
|
|
||||||
Построить область, площадь которой выражается интегралом |
||||||||||||||||
a |
2a2 x2 |
|
|
интеграл. |
|
|
|
|
|
|
||||||
dx |
dy . Вычислить |
этот |
|
|
Поменять |
порядок |
||||||||||
0x
интегрирования. |
|
|
|
|
о |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|||
2. |
Определить |
объем |
телар, ограниченного |
поверхностями |
||||||||||||||||
x2 |
|
|
y2 |
z2 |
|
0; x2 |
y2 |
|
z2 |
a2 |
(внутри конуса). |
|
|
|
|
|||||
|
|
|
|
|
|
|
дуги |
|
|
|
|
x2 |
|
|
|
|
|
|||
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
Найти массу |
|
|
параболы y |
2 |
, лежащей между точками |
||||||||||||||
1, 1 и |
2,2 |
, если плотность равна |
y |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
2 |
п |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
Вычислитьо xy2dx |
yz2dy |
x2zdz , |
где L – |
отрезок прямой |
|||||||||||||||
Р |
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OB;O 0, 0, 0 ; B |
2, 4, 5 . |
|
|
|
|
|
|
|
|
|
|
|||||||||
5. |
С помощью формулы Остроградского, вычислить |
x |
2 |
dydz |
||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
y |
2 |
dxdz |
z |
2 |
dxdy |
|
где |
|
S |
– |
внешняя |
сторона куба |
||||||||
|
|
|
|
|||||||||||||||||
0 x a; 0 y a; 0 z a . |
|
|
|
|
|
|
|
|
||||||||||||
6. |
|
|
|
|
, если |
|
|
|
|
|
|
|
|
|
||||||
Найти rota |
a |
x3zi |
y3xj |
z3xk . |
|
|
|
|
||||||||||||
85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
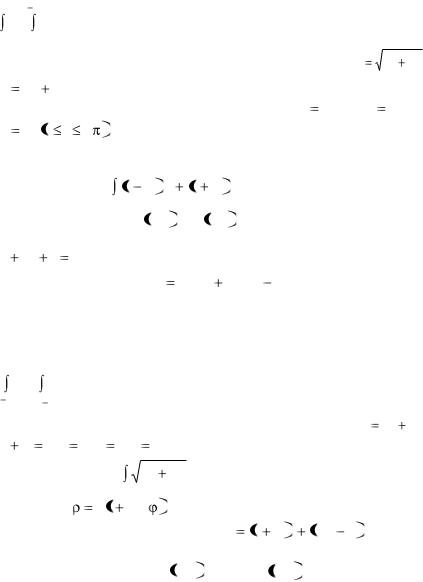
Вариант 28
1. Построить область, площадь которой выражается интегралом
1 2 x2
dx dy . Изменить порядок интегрирования. Вычислить интеграл.
0x
|
2. |
Вычислить объем тела, ограниченного поверхностями z |
x2 |
y2 ; |
|||||||||||||||||
|
|
|
y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
z |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
Уa sin t; |
||||
|
3. |
Найти |
массу |
винтовой |
линии |
|
|
x a cost; y |
|||||||||||||
z |
bt |
0 |
t |
2 , |
если |
плотность |
в |
|
каждой |
ее |
точке |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||
пропорциональна квадрату расстояния этой точки до начала |
|||||||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4. |
Вычислить |
x |
y dx |
|
x |
|
y dy , где |
L |
– отрезок прямой |
|
||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
той |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соединяющий точки A 2, 3 |
и B 3, 5 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
5. |
Вычислить |
площадь |
|
поверхности |
|
|
|
части |
плоскости |
|||||||||||
|
2y |
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|||||
x |
z 4 , которая расположена в первом октанте. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|||
|
6. |
Найти rotF , если F |
y |
|
z |
|
i |
4xz |
j |
xy |
|
k . |
|
|
|
|
|||||
|
|
|
|
|
|
|
Вариант 29 |
|
|
|
|
|
|
|
|
||||||
|
1. |
Построить областьит, площадь которой выражается интегралом |
|||||||||||||||||||
00
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
dx . И менить порядок интегрирования. Вычислить интеграл. |
|||||||||||
|
|
п |
з |
|
|
|
|
|
|
|
|
|||
2 |
|
y |
2 4 |
|
|
|
|
|
|
|
|
|
||
|
2. |
|
Вычислить бъем тела, ограниченного поверхностями z |
x2 y2; |
||||||||||
е |
|
0; y |
L |
0 . |
|
|
|
|
|
|
|
|||
x |
y |
|
4; x |
0; z |
|
|
|
|
|
|
|
|||
Р |
|
Вычислить |
|
x2 |
y2 dl , |
где |
|
– |
верхняя |
половина |
||||
|
3. |
|
|
L |
||||||||||
кардиоиды |
a 1 |
cos . |
|
|
|
|
|
|
|
|||||
|
4. |
|
Поле |
образовано |
силой |
|
. |
Найти |
||||||
|
|
F |
x |
y i |
2xy 8 j |
|||||||||
работу поля при перемещении материальной точки массы |
m по |
|||||||||||||
дуге окружности от точки |
a, 0 до точки |
0, a . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
86 |

|
5. |
Вычислить |
массу |
поверхности |
z2 |
x2 |
y2 , |
заключенной |
|||||||||||||
между плоскостями |
z |
0 |
и z |
1, |
если поверхностная плотность |
||||||||||||||||
пропорциональна x2 |
y2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
6. |
Найти |
|
циркуляцию |
поля |
|
по |
контуру |
окружности |
||||||||||||
|
|
F |
|
yi |
|||||||||||||||||
x |
2cost; y |
|
2 |
|
2sin t . |
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 30 |
|
|
|
|
Т |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1. |
Вычислить площадь фигуры, ограниченную линиями ax |
y2 2ay; |
||||||||||||||||||
x |
y |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2. |
Определить массу |
тела, |
|
ограниченного |
поверхностями |
|||||||||||||||
az |
a |
2 |
x |
2 |
|
2 |
; z |
0 , |
если плотность его |
в |
Н |
точке |
|||||||||
|
|
|
y |
каждой |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
||
пропорциональна аппликате этой точки. |
|
|
|
|
|
|
|||||||||||||||
|
3. |
Вычислить |
|
|
|
по |
и |
|
|
прямоугольника, |
|||||||||||
|
|
xydl |
|
пер метру |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L |
|
р |
|
|
|
|
|
|
|
||
ограниченного прямыми |
x |
0; y |
0; x |
|
4; y |
2. |
|
|
|
||||||||||||
|
4. |
Вычислить |
|
|
о |
, |
где |
L |
– |
верхняя половина |
|||||||||||
|
|
x y dx dy |
|||||||||||||||||||
расположена в первомоктанте. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
окружности |
x2 |
|
y2 |
R2 |
(в п л жительном направлении). |
|
|||||||||||||||
|
5. |
Найти |
|
|
|
и |
|
|
|
|
|
2x |
|
|
4 , |
которая |
|||||
|
|
площадь час и поверхности |
y |
z |
|||||||||||||||||
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|||
|
6. |
|
|
о |
|
|
|
|
|
|
|
|
ln x |
2y |
3z . |
||||||
|
Найти дивергенц ю градиента функции u |
||||||||||||||||||||
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е |
|
II. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ.ТЕОРИЯ |
|||||||||||||||||||
|
|
|
ВЕРОЯТНОСТЕЙ. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ |
||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
СТАТИСТИКИ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
З а н я т и |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Преобразование Лапласа. Изображение элементарных функций.
Основные теоремы
87
Аудиторная работа
Всюду в дальнейшем под заданной с помощью формулы функцией f (t) будем понимать произведение этой функции на
функцию Хевисайда:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1(t) |
|
1, |
t |
0, |
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
t |
0, |
|
|
|
|
|
Т |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
т. е. считать |
|
f (t) |
|
0 при t |
0 . |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Н |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.1. Проверить, являются ли следующие функции оригиналами: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
г. et 3 . |
Б |
|
1 |
||||||
а. e5t . |
б. |
|
|
|
|
. |
|
|
в. e4t 1 . |
|
|
д. t 3 . |
е. e t . |
|||||||||||||||
|
|
|
|
|
t |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|||
1.2. Используя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
определение преобразования Лапласа, найти |
|||||||||||||||||||||||||
изображение оригинала: |
|
|
|
р |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1, |
|
|
0 t |
|
2, |
|
|
|
|
t |
, |
0 |
t |
1, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подобия |
|
|
|
|
|
|
|
|
|
|
|||
а. f (t) |
|
|
1, 2 t |
|
3, |
|
|
иб. f (t) |
|
|
1, 1 t |
2, |
|
|||||||||||||||
|
|
|
|
0, |
|
|
|
3 |
|
|
t. |
|
|
|
|
|
|
|
|
|
0, |
2 |
|
t. |
|
|||
|
|
|
|
|
|
|
и |
|
|
|
|
, найти изображение оригинала |
||||||||||||||||
1.3. Пользуясь теоремой |
|
|
|
|||||||||||||||||||||||||
а. |
sin 5t . |
|
|
з |
т |
|
б. cos3t . |
|
|
|
|
|
|
|||||||||||||||
|
о2 |
|
|
2 |
|
|
|
|
|
|
запаздывания, |
|
найти |
изображение |
||||||||||||||
1.4. Поль уясь |
|
|
|
теоремой |
|
|
||||||||||||||||||||||
оригинала: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
et a sin(t |
|
a), |
|
0, t |
|
|||||
а. |
sin(t |
|
|
), |
t |
|
|
|
|
. |
|
|
|
|
|
б. |
|
a |
a . |
|||||||||
1.5. Применяя теорему запаздывания, найти оригинал для функции: |
||||||||||||||||||||||||||||
Р |
|
|
pe 2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
еа. |
|
|
. |
|
|
|
|
|
|
|
|
|
б. |
|
. |
|
|
|
|
|
|
|||||||
|
p2 1 |
|
|
|
|
|
|
|
|
|
p2 4 |
|
|
|
|
|
|
|||||||||||
1.6. Используя |
|
|
свойства |
|
преобразования |
|
Лапласа и |
таблицу |
||||||||||||||||||||
изображений основных функций, найти изображения заданных функций:
88
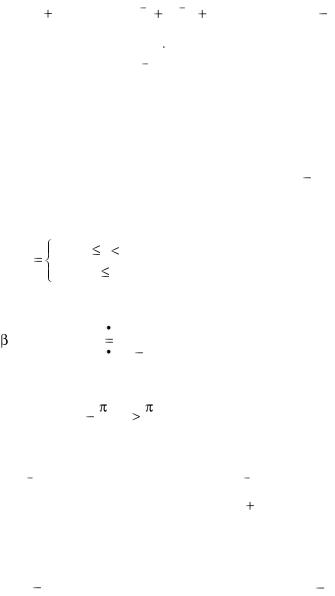
а. |
1 |
t |
2 |
|
|
1. |
|
|
|
|
|
|
б. |
e |
t |
3e |
2t |
t |
2 |
. |
|
|
|
в. |
2sin t |
|
cos |
t |
. |
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
г. |
cos2 t . |
|
|
|
|
|
|
|
д. |
sh 3t |
cos2t . |
|
|
|
|
|
е. t3e2t . |
|
|
|
|
|||||||||||||||||||||||
ж. t2c h 2t . |
|
|
|
|
|
з. te t sh t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Домашнее задание |
|
|
|
|
t |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||
1.7. Проверить, являются ли следующие функции оригиналами: |
||||||||||||||||||||||||||||||||||||||||||||
а. |
sin 3t . |
|
|
|
|
|
|
|
б. |
sh 2t . |
|
|
|
|
|
|
|
|
|
|
в. |
|
|
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 9 |
|
|
|
||||||||||||||||||||||||
1.8. Используя определение преобразования Лапласа, найти |
||||||||||||||||||||||||||||||||||||||||||||
изображение оригинала: |
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
Н |
|
|||||||||||||||||||||||||||
f (t) |
|
|
|
|
et , 0 t 1, |
|
|
|
|
|
|
|
|
|
|
найти |
|
|
Б |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1, |
|
1 |
|
t. |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.9. Пользуясь теоремой подоб я, |
|
|
|
изображение оригинала |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sh t , зная, что sh t |
|
|
|
|
|
. |
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
p2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.10. |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Пользуясь |
|
|
еоремой запаздывания, найти изображение |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
оригинала |
cos(t |
|
|
2 |
), t |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
e |
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.11. Применяя теорему запаздывания, найти оригинал для функции: |
||||||||||||||||||||||||||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а. |
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
Р |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p |
1) |
|
|
|
|
|
|
|
|
|
|
|||
1.12. Используя свойства преобразования Лапласа и таблицу |
||||||||||||||||||||||||||||||||||||||||||||
изображений основных функций, найти изображения заданных |
||||||||||||||||||||||||||||||||||||||||||||
функций: |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а. |
t |
2 |
|
|
|
e |
t |
. |
|
|
|
|
|
|
|
б. sin |
2 |
2t . |
|
|
|
|
|
|
в. |
sin3t |
t cost . |
|||||||||||||||||
2
Ответы
89
