
metodichkaFTUG_chast1
.pdf
b m 2n 3 2 2, 4 3 2, 2 2 2 1, 2, 2 .
Скалярное произведение a,b 1 1 1 2 0 2 3 .
Вычислим длины векторов:
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 12 02 |
|
, |
|
b |
|
12 2 2 22 3 . |
||||
a |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Тогда cos a,b |
a,b |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a |
|
b |
|
3 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и b : a,b |
|
|
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
Угол между векторами |
a |
arccos |
|
|
|
|
. |
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) Найдем скалярное произведение
a,b 2m 3n,4m 3n 8 m, m 18 m, n 9 n, n =
8 m 2 18 m n cos 3 9 n 2 8 9 18 3 4 12 9 16 108 .
Найдем длину вектора a
a 
 2m 3n, 2m 3n
2m 3n, 2m 3n 
 4 m, m 12 m, n 9 n, n
4 m, m 12 m, n 9 n, n
 4 m 2 12 m n cos 3 9 n 2
4 m 2 12 m n cos 3 9 n 2 
 4 9 12 3 4 12 9 16
4 9 12 3 4 12 9 16
 108 6
108 6
 3 .
3 .
Найдем длину вектора b
b 
 4m 3n,4m 3n
4m 3n,4m 3n 
 16 m, m 24 m, n 9 n, n
16 m, m 24 m, n 9 n, n
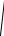 16 m 2 24 m n cos 3 9 n 2
16 m 2 24 m n cos 3 9 n 2 
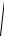 16 9 24 3 4 12 9 16
16 9 24 3 4 12 9 16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
144 12 . |
|
|
|
||||||
Тогда cos a,b |
a,b |
|
|
108 |
|
|
|
|
|
|||||
|
|
|
|
3 |
. |
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
|
b |
6 |
|
3 12 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51

|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|||||
Угол между векторами a |
и b : a,b arccos |
|
|
|
|
. |
|||
|
|
|
|
||||||
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|||
|
|
Пример |
3. |
|
Найдите |
вектор |
b , |
|
коллинеарный |
вектору |
||||||||||||||
a 1, 2, 2 и удовлетворяющий условию ( b, a) 2 . |
|
|
||||||||||||||||||||||
|
|
Решение. |
Обозначим вектор b b1 ,b2 ,b3 , тогда из условия |
|||||||||||||||||||||
|
|
|
b1 2b2 2b3 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
задачи |
|
b |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
b1 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
или |
b2 2b1; b3 2b1; 9b1 2; b1 |
2 / 9 , |
тогда |
|||||||||||||||||||
b2 b3 4 / 9 . Итак: b 2 / 9, 4 / 9, |
4 / 9 . |
|
|
|||||||||||||||||||||
|
|
Пример |
4. |
|
Найти |
|
проекцию |
вектора |
a 3i 4 j k |
на |
||||||||||||||
направление вектора b i j . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Решение. |
|
|
Так |
как |
|
a,b 3 1 4 1 ( 1) 0 7 |
и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
b |
12 12 02 2 , то |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a a,b |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
пр |
|
7 |
|
|
7 2 |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 5. Даны векторы: a 3, 3, 2 , b 4,1, 0 . Найти
a, b , a,b , прb a , прa b .
Решение. Найдем скалярное произведение и длины векторов
a и b :
a,b 3 4 3 1 2 0 15 ,
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
9 9 4 22, |
b |
|
16 1 17 . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
52

Так как cos a,b |
|
|
a,b |
|
|
|
15 |
|
|
|
|
|
|
|
|
15 |
|
, то угол между |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
a |
|
b |
|
|
22 |
17 |
374 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
||||||||||||||
векторами a и b равен a,b arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
374 |
|
|
|
|||||||||||||||
Найдем проекцию вектора a на направление вектора b |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
пр |
|
a a,b |
|
|
15 |
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдем проекцию вектора b на направление вектора a |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
пр |
|
b a,b |
|
|
15 |
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример |
6. |
На |
|
материальную |
|
|
|
точку |
|
действуют силы |
|||||||||||||||||||||||||
F1 j, F2 i , |
F3 k . |
|
|
Найти |
|
работу |
|
равнодействующей |
|||||||||||||||||||||||||||
этих сил R при перемещении точки из положения A 2, 1, 0 в |
|||||||||||||||||||||||||||||||||||
положение B 4,1, 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
Найдем силу |
|
R F1 |
F2 F3 i j k |
и вектор |
||||||||||||||||||||||||||||||
перемещения: |
AB 2i 2 j k . |
Tогда |
|
искомая |
работа |
||||||||||||||||||||||||||||||
A R, AB 1 2 1 2 1 1 3 .
Задания для решения в аудитории
I уровень
1. Найти скалярное произведение векторов a 6i 3 j 4k и
b4i 2 j 2k .
2.Известно, что a 1, b 2, (a,b) 3 . Найти: a) (a, a 2b) ;
б) (a 2b,3a b ) ; 2a 3b .
3. Найти длину вектора a 3m 4n , зная, что m и n – взаимно перпендикулярные орты.
53

4. Даны векторы a и b такие, что a 11, b 23, a b 30 .
Найти |
a b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
Даны |
вершины |
|
|
|
|
|
четырехугольника: |
||||
|
|
|
|
|
|
|
||||||||
A(1,2,3), B(7,3,2), C( 3,0,6), D(9,2,4) . |
|
|
|
Доказать, что |
его |
|||||||||
диагонали взаимно перпендикулярны. |
|
|
|
|
|
|
|
|
|
|||||
6. |
Найти длины диагоналей параллелограмма, построенного |
|||||||||||||
на векторах a 2 p q и b p 2q , где |
|
p |
|
|
|
q |
|
1 и ( p, q) |
. |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
7. |
Найти острый угол между диагоналями параллелограмма, |
|||||||||||||
построенного на векторах a 6, 1,1 |
и b 2,3,1 . |
|
||||||||||||
8. |
Вычислить проекцию вектора |
a 5, 2,5 на ось вектора |
||||||||||||
b 2, 1, 2 . |
|
|
|
|
|
|
|
|
|
|
|
|||
9. |
Даны силы F1 i j k и F 2 |
2i j 3k . Найти работу |
||||||||||||
их равнодействующей при перемещении точки из начала координат в точку M (2, 1, 1) .
10. Определить, при каком значении векторы |
3a b и |
|||||||
a 2b будут взаимно перпендикулярными, где |
|
|
|
|
|
|
|
2 и |
|
a |
|
2, |
b |
||||
|
|
|||||||
|
|
|
|
|
|
|
|
|
(a,b) 4 .
11. В плоскости Oyz найти вектор a , перпендикулярный вектору b 2, 2,1 и имеющий с ним одинаковую длину.
II уровень
1. Векторы a и b взаимно перпендикулярны, а вектор c
образует с ними углы / 3. Зная, что |
|
a |
|
|
b |
2, |
|
c |
|
1, найти: |
|
|
|
|
|||||||
a) (2a b,c a) ; б) (a b c )2 . |
|
|
|
|
|
|
|
|
|
|
54

2. |
Вычислить |
угол между |
векторами |
a 3p 2q |
и |
|||
b p 5q , где p |
и q - единичные взаимно перпендикулярные |
|||||||
векторы. |
|
|
|
|
|
|
|
|
|
3. Для каких векторов |
a и |
b |
векторы |
a b |
и a b |
||
ортогональны. |
|
|
|
|
|
|
|
|
4. |
Найти вектор u , перпендикулярный векторам a i k |
и |
||||||
b 2 j k , если |
известно, |
что |
его |
проекция на |
вектор |
|||
c i |
2 j 2k равна единице. |
|
|
|
|
|
|
|
5.Найти вектор u , коллинеарный вектору a 1, 2,3 и
удовлетворяющий условию (u,c) 5 , где c 1, 0,1 .
6.Найти проекцию вектора a 2, 3, 4 на ось, образующую равные углы с осями координат.
Задания для самостоятельного решения
1. Вычислить скалярное произведение двух векторов ( p, q) , зная их разложение по трем единичным взаимно перпендикулярным векторам a, b и c : p 3a b 2c ; q a 4b 5c .
2. Векторы a, b, c попарно образуют друг с другом углы,
каждый из которых равен 600 . Зная, что a 4, b 2 и c 6 ,
определить модуль вектора p a b c . 3. Найти угол между векторами:
а) a 2, 4, 4 и b 3, 2, 6 ; б) a 1,3, 
 6 и b 1,1, 0 ;
6 и b 1,1, 0 ;
в) a 
 2,1,1 и b 1,0,0 .
2,1,1 и b 1,0,0 .
55

4.В треугольнике с вершинами в точках A(3,2, 3), B(4,3, 3)
иС(3,1, 4) найдите величину его угла при вершине А и длину
медианы AN.
5. Найти вектор x , удовлетворяющий условиям
|
|
а) |
x коллинеарен a 3, 2, 2 |
и x, a 34 ; |
|
|
|
|
|
||||||||||||||
|
|
б) |
x перпендикулярен a 3,1,5 , при этом |
|
|
|
|
|
|||||||||||||||
x,2i 3 j 6k 2 и x, k 6 ; |
|
|
|
|
|
|
|||||||||||||||||
|
|
в) |
x перпендикулярен |
оси |
|
Оy , |
x, a 5 , |
x,b 3 , где |
|||||||||||||||
a 2,1,3 , b 1, 2, 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. |
Даны векторы |
a 1, 3, 4 , b 3, 4, 2 |
и c 1,1, 4 . |
||||||||||||||||||||
Вычислить прb c a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
|
Даны |
векторы |
|
|
a |
|
и |
b такие, |
что |
|
a |
|
13, |
|||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
b |
19, |
a b |
|
24 . Найти |
|
a b |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||||
8. |
Пусть |
a и |
− |
|
|
единичные векторы. |
Вычислить |
||||||||||||||||
3a 4b,2a 5b , если |
|
a b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.Длины ненулевых векторов a и b равны. Найдите угол между векторами a и b , если векторы p a 3b и q 5a 3b ортогональны.
10.Даны силы M 3, 4, 2 , N 2,3, 5 и P 3, 2, 4 ,
приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения M1 (5, 3, 7) в положение M2 (4, 1, 4) .
56

|
5 |
|
|
|
|
|
3 |
|
|
|
|
|
Ответы. 1. 9. 2. 10. 3. а) arccos |
|
; б) |
; в) |
|
|
. 4. 2 3, 2 2 . |
||||||
21 |
4 |
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
5. а) 6, 4, 4 ; б) |
8, 6,6 ; в) |
1, 0,1 . |
6. |
5. |
7. 22. 8. 21 2 . |
|||||||
9.arccos 7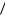 9 . 10. 13
9 . 10. 13
2.3.Векторное произведение векторов. Смешанное произведение векторов.
Упорядоченная тройка некомпланарных векторов a, b, c называется правой (левой), если при совмещении их начал кратчайший поворот от a к b виден из конца вектора c как поворот против часовой стрелки (по часовой стрелке).
Векторным |
произведением вектора a на вектор b |
||||||||||
называется |
|
вектор |
a,b , длина и направление которого |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
определяются условиями: |
|
||||||||||
|
|
a,b |
|
|
|
|
|
|
|
||
1. |
|
|
|
a |
|
b |
sin , |
где - угол между a и b . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
a,b |
a , |
|
a,b |
b . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
3. |
a, b, a,b |
|
− правая тройка векторов. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Свойства векторного произведения
1.a,b b, a ;
2.a b,c a,c b,c , a,b c a,b a,c ;
3.a,b a, b a,b ;
4. |
a,b |
0 |
a b (равенство нулю векторного |
|
|
|
|
|
|
произведения означает коллинеарность векторов). Геометрический смысл векторного произведения: длина
вектора a,b численно равна площади параллелограмма построенного на векторах a и b , приведенных к общему
57
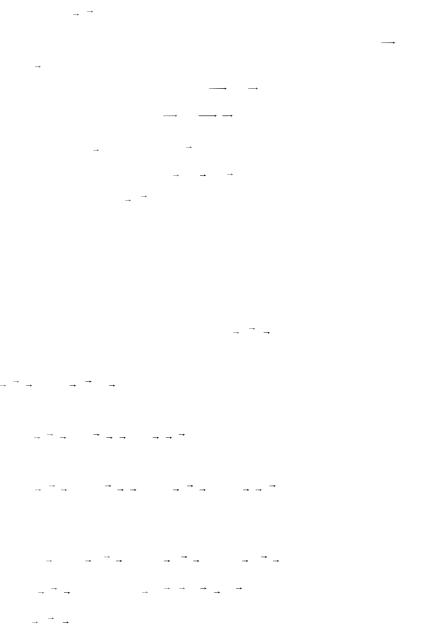
началу |
S |
a,b |
. |
|
|
|
|
|
|
Физический смысл векторного произведения: момент M силы F , приложенной к точке A относительно точки O, есть векторное произведение векторов OA и F , т. е.
M OA, F .
Если вектор a a1 , a2 , a3 , b b1 ,b2 , b3 , то
|
|
|
i |
j |
k |
|
|
a, b |
|
a |
a |
a |
. |
(2.10) |
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
b1 |
b2 |
b3 |
|
|
Векторное произведение можно применять при нахождении какого-либо вектора, ортогонального двум данным, при вычислении площадей параллелограмма и треугольника, при вычислении моментов силы относительно точки.
Смешанным |
|
произведением a, b, c трех |
векторов |
называется число, определяемое следующим |
образом: |
||
|
|
,c . |
|
a,b,c a, b |
|
|
|
Свойства смешанного произведения
1. a,b,c b,c, a c, a,b . При циклической перестановке сомножителей смешанное произведение не изменяется;
2. a,b,c b, a,c c,b, a a,c,b . При перестанов-
ке двух сомножителей смешанное произведение меняет знак на обратный;
3. |
1a1 2a2 ,b,c |
1 a1,b,c 2 a2 ,b,c , где 1, 2 R; |
4. |
a,b,c 0 при |
a 0, b 0, c 0 тогда и только тогда, |
когда a, b, c – компланарные векторы;
58

5. если |
a,b,c 0 , |
то |
векторы |
a, b, c |
образуют |
базис в |
||||
трехмерном пространстве; |
|
|
|
|
|
|
|
|
||
6. если |
a,b,c 0 , |
то |
векторы |
a, b, c |
образуют |
правую |
||||
тройку; если a,b,c 0 |
– левую. |
|
|
|
|
|
||||
Если |
векторы |
заданы |
|
своими |
координатами: |
|||||
a a1 , a2 , a3 , b b1 ,b2 , b3 , с с1 ,с2 ,с3 то |
|
|
||||||||
|
a, b, |
c |
|
a1 |
a2 |
a3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
b1 |
b2 |
b3 |
. |
|
(2.11) |
|||
|
|
|
|
|
c1 |
c2 |
c3 |
|
|
|
Геометрический смысл смешанного произведения: абсолютное значение a,b,c равно объему V параллелепипеда,
построенного на векторах a, b, c , приведенных к общему началу: V a,b,c . Объем пирамиды, построенной на
векторах a, b, c равен V 16 a,b,c .
Смешанное произведение можно применять при вычислении объёмов параллелепипеда, пирамиды, длин их высот.
Пример 1. Найти координаты векторного произведения
2a 3b,2a 4b , если a 3i j 2k , |
b 2i j k . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Найдем |
2a 3b (0, 1, 1) |
и |
|
|
2a 4b 2, 2, 0 . |
|||||||||||||||
Векторное произведение, по определению, равно |
|||||||||||||||||||||
|
i |
j |
|
k |
|
i |
|
1 |
1 |
|
j |
|
0 |
1 |
|
k |
|
0 |
1 |
|
2i 2 j 2k . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 1 |
1 |
|
|
|
|
|
|
|
||||||||||||
|
2 |
2 |
|
0 |
|
|
|
2 |
0 |
|
|
|
2 |
0 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59

Пример 2. Пусть |
|
|
|
|
|
|
|
q |
|
3, p, q 4 . Найти |
|||||||||||||||||||||
|
p |
2, |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
a) |
|
p,q |
|
; б) |
|
p q, p q |
|
; в) |
|
p 2q,3p q |
|
. |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение. а) По определению векторного произведения |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin p, q |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
p, q |
|
|
|
|
|
|
|
2 |
3 ; |
|||||||||||||||||
|
|
|
|
|
|
p |
|
q |
2 3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) Используя алгебраические свойства векторного произведения, имеем:
p q, p q p, p q, p p, q q, q0 p, q p, q 0 2 p, q ,
p q, p q 2 p, q 2 p
 q sin p, q 2 3 6 ;
q sin p, q 2 3 6 ;
в) Используя алгебраические свойства векторного
произведения, имеем:
p 2q,3 p q 3 p, p 6 q, p p, q 2 q, q
0 6 p, q p, q 0 7 p, q ,
p 2q,3p q 7 p,q 7 3 21.
Пример |
3. Силы F1 2i j 5k |
и F2 3i 5 j k |
|
приложены к точке A 3, 4, 1 . Вычислить величину момента |
|||
равнодействующей этих сил R относительно точки B 1, 3, |
0 . |
||
Решение. |
Найдем силу R F1 F 2 i 4 j 4k и |
плечо |
|
BA 2i j k . Момент сил M вычисляется по формуле
60
