4_Лабораторные, контрольные и самостоятельные работы по информатике_2010

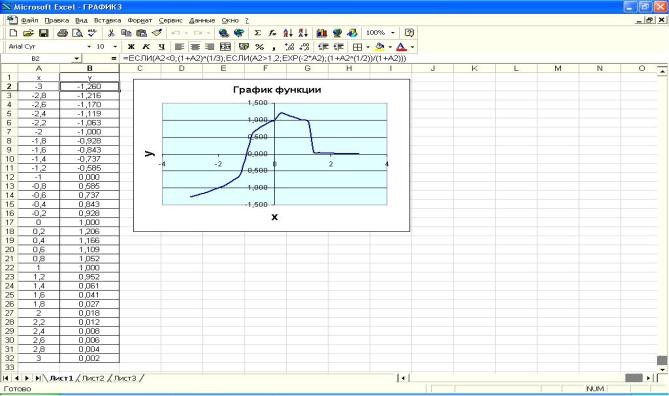
Самостоятельная работа «Построение графика функции с условиями»

при x [-3, 3]

Для построения графика функции (рис. 4.13) необходимо сначала по-

строить таблицу ее значений при различных значениях аргумента, причем обычно аргумент изменяется с фиксированным шагом. Шаг выбирают не-

большим, чтобы таблица значений функций отражала их поведение на интервале табуляции. В нашем случае будем считать, что шаг изменения аргу-

мента равен 0,2. Необходимо найти: y(-3), y(-2,8), y(-2,6), …, y(3). С этой це-

лью в диапазон ячеек А2:А32 введём автозаполнением следующие значения переменной х: -3; -2,8; -2,6; …; 3. В ячейки A1 и B1 введём заголовки столбцов: x и y.

В ячейку В2 вводится формула: =ЕСЛИ(А2<0;(1+A2)^(1/3);ЕСЛИ(A2>1,2;EXP(-*A2);(1+A2^(1/2))/(1+A2)))

Рис. 4.13. График функции с двумя условиями

71

Самостоятельная работа « Построение двух графиков в одной

системе координат»

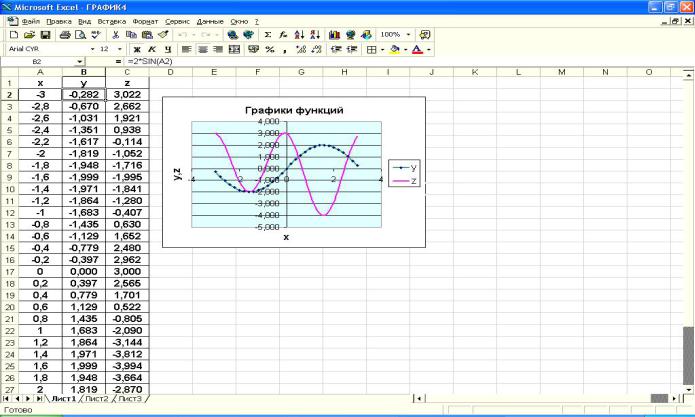
Построить в одной системе координат графики следующих двух функций:

= 2*sin(A2) =3*cos(2*A2) – sin(A2)

Выделим диапазон B2:C2, установим указатель мыши в его правом нижнем углу и с помощью автозаполнения скопируем формулы в ячейки B3:C32.

Выделим диапазон ячеек A1:C32, вызовем Мастер диаграмм. Выберем тип диаграммы – Точечная и вид графика. На втором шаге Мастера диаграмм в

группе Ряды данных установим переключатель в положение В столбцах. На третьем шаге Мастера диаграмм в поле Название диаграммы вводим Графики функций, в поле Ось x – x, в поле Ось y – y и z. Нажатие кнопки Готово завер-

шает построение графиков (рис.4.14).

Рис. 4.14. График двух функций в одной системе координат

72

Графики функций y и z могут для наглядности различаться по типу линий.

Для этого график, внешний вид которого мы хотим изменить, выделяется и с помощью Контекстного меню вызывается диалоговое окно Форматирование элемента данных, которое позволяет изменять тип, толщину и цвет линии, а

также тип, цвет и фон маркера.

Самостоятельная работа «Нахождение корней уравнения»

Найти все корни уравнения

x3 – 0.01x2 – 0.7044x + 0.1391 = 0

У полинома третьей степени имеется не более трех вещественных корней.

Для нахождения корней их предварительно нужно локализовать, т.е. опреде-

лить интервалы, на которых они расположены. С этой целью построим график функции

y = x3 – 0.01x2 – 0.7044x + 0.1391

на отрезке [-1,1] с шагом 0.1. В столбец А введем значения x, в столбец В – зна-

чения y, вычисленные по формуле (рис. 4.15): = A2^3 – 0.01*A2^2 – 0.7044*A2 + 0.1391

Рис. 4.15. Локализация корней полинома

73

Из рисунка видно, что полином меняет знак на интервалах: [-1, -0.8], [0.2, 0.3], [0.7, 0.8]. Это значит, что на каждом из них имеется корень данного уравнения. Поскольку полином третьей степени имеет не более трех действи-

тельных корней, мы локализовали все его корни. Найдем их методом последо-

вательных приближений с помощью команды Сервис/ Подбор параметра. Но,

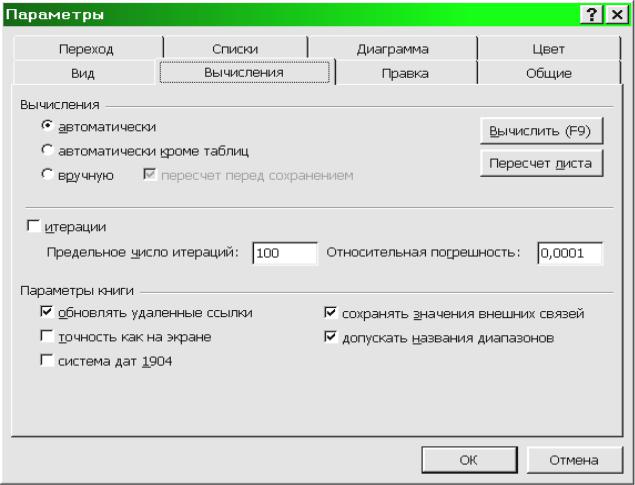
прежде всего, зададим относительную погрешность и предельное число итера-

ций равными, например, 0.0001 и 1000. Эти параметры Excel задаются с помо-

щью команды Сервис/ Параметры – на вкладке Вычисления (рис. 4.16).

Рис. 4.16. Вкладка Вычисления диалогового окна Параметры

В качестве начальных приближений можно взять любые точки из отрезков локализации корней, например, точки: -0.95, 0.25 и 0.75. Введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу:

= C2^3 – 0.01*C2^2 – 0.7044*C2 +0.1391

Выделим эту ячейку и, с помощью маркера заполнения распространим введен-

ную в нее формулу на диапазон D2:D4. Таким образом, в ячейках D2:D4 вы-

числяются значения полинома при значениях аргумента, введенного в ячейки

74

C2:C4 соответственно. Теперь выберем команду Сервис/Подбор параметра и

заполним диалоговое окно Подбора параметра (рис. 4.17) следующим образом.

Рис. 4.17. Диалоговое окно

Подбор параметра

В поле Установить в ячейке введем D2. Отметим, что в этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. Для нахождения корня уравнения с помощью подбора значе-

ния параметра, надо записать уравнение так, чтобы его правая часть не содер-

жала переменную.

В поле Значение введем 0 (в этом поле указывается правая часть уравне-

ния). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную). Вводить ссылки на ячейки в поля диало-

гового окна Подбор параметра удобнее не с клавиатуры, а щелчком на соот-

ветствующей ячейке. При этом Excel автоматически будет превращать их в аб-

солютные ссылки (в нашем примере $D$2, $C$2).

После нажатия кнопки OK процедура подбора параметров находит при-

ближенное значение корня, которое помещает в ячейку С2. В данном случае оно равно -0.920. Как выглядит диалоговое окно Результат подбора парамет-

ра после завершения поиска решения, показано на рис. 4.18.

Рис. 4.18. Диалоговое окно Результат подбора параметра

Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны

0.210 и 0.720.

75

Самостоятельная работа «Решение системы линейных уравнений»

Дана система линейных уравнений: 2х1+3х2+7х3+6х4=1 3х1+5х2+3х3+х4=3 5х1+3х2+х3+3х4=4 3х1+3х2+х3+6х4=5

Пусть матрица записана в ячейки А10:D13, а свободные члены - в ячейки

F10:F13.

В Excel имеются следующие функции для работы с матрицами:

МОБР – обращение матрицы,

МОПРЕД – вычисление определителя матрицы,

МУМНОЖ – матричное произведение двух матриц,

ТРАНСП – транспонирование матрицы.

Решение линейной системы АХ=В, где А - матрица коэффициентов, В -

столбец (вектор) свободных членов, Х - столбец (вектор) неизвестных, имеет вид Х=А-1В, где А-1 - обратная матрица.

Выделите под вектор решений диапазон G10:G13 и введите формулу: =МУМНОЖ(МОБР(А10:D13); F10:F13)

Для получения решения нажмите Ctrl + Shift + Enter ; сделайте про-

верку решения: в первое уравнения подставьте значения корней.

Самостоятельная работа «Построение уравнения линейной регрессии»

Имеются две наблюдаемые величины x и y, например, объем реализации фирмы, торгующей автомобилями, за шесть недель ее работы. Значения на-

блюдаемых величин приведены в таблице, где x – отчетная неделя, а y – объем

76

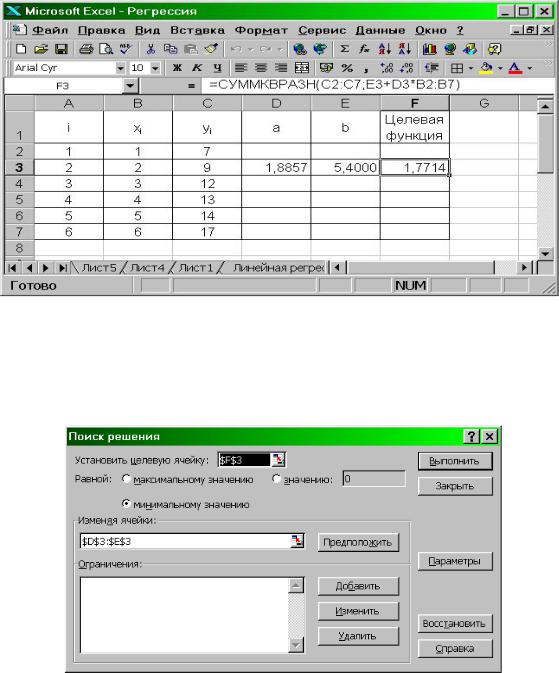
данных значений yi от соответствующих значений, вычисляемых с помощью уравнения регрессии. Для решения этой задачи в ячейки D3:E3 вводим ориен-

тировочные значения коэффициентов a, b (например, a=2, b=2), а в ячейку F3 (рис. 4.19) вводим целевую функцию СУММКВРАЗН(C2:C7;E3+D3*B2:B7).

Рис. 4.19. Вычисление коэффициентов уравнения регрессии с использованием целевой функции

Выбираем команду Сервис/Поиск решения и заполняем диалоговое окно

Поиск решения (рис. 4.20).

Рис. 4.20. Диалоговое окно Поиск решения

Результат нахождения параметров a и b – на рис. 4.20. Полученное уравне-

ние регрессии: y = 1,8857x + 5,4.

Другой способ получения уравнения линейной регрессии основывается на по-

строении линии тренда. Построим точечный график по диапазону ячеек B2:C7,

77

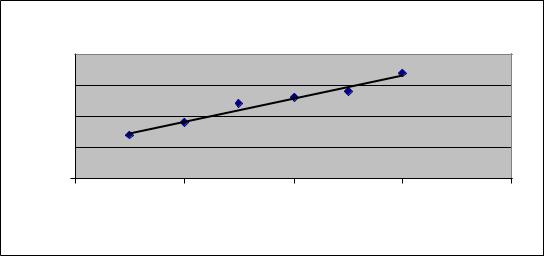
выделим точки графика двойным щелчком, а затем щелкнем правой кнопкой мыши. В появившемся контекстном меню выберем команду Линии тренда.

Выберем Тип/Линейная, а на вкладке Параметры установим флажки: Помес-

тить уравнение на диаграмме, Поместить на диаграмму величину достовер-

ности аппроксимации (R2). На рис. 4.21 – результат построения линии тренда.

Коэффициент R2 характеризует ту долю дисперсии (изменений) функции y, ко-

торая прогнозируется с помощью найденного уравнения регрессии. Этот коэф-

фициент называют ещё коэффициентом детерминации. По его величине судят о том, можно ли использовать уравнение регрессии для прогнозирования.

Для прогноза с помощью уравнения регрессии используется встроенная функция ТЕНДЕНЦИЯ(<известные y>;<известные x>;<новые x>), которая вы-

числяет ожидаемые новые значения y для новых x, если известны некоторые опытные значения x и y. Вычисления делаются в предположении, что x и y за-

висят линейно. Вычислите ожидаемый объем реализации автомобилей за 7-ю, 8-ю и 9-ю недели работы фирмы.

В рассматриваемой задаче объем реализации автомобилей (y) был дан за 6

недель (x= 1,2,...,6). Так как результат должен выводиться в три ячейки, значит функция ТЕНДЕНЦИЯ() должна вводиться как функция обработки массива.

Выделяется диапазон ячеек C8:C10 (рис. 4.22), вводится функция ТЕНДЕНЦИЯ() и нажимаются клавиши Ctrl+Shift+Enter (вместо обычного Enter). Результат прогноза виден на рис. 4.22.

78

где aij, bi, cj (i=1, 2,…, m; j=1, 2, … , n) – заданные постоянные числа.

Обычно в задачах линейного программирования на переменные налагаются

еще условия неотрицательности: xj 0 (j=1, 2, …, n).

Линейная функция z называется целевой функцией или функцией цели, а

дополнительные условия называются ограничениями. Решение задачи линей-

ного программирования состоит в нахождение переменных xj, которые удовле-

творяют системе ограничений и минимизируют (максимизируют) целевую функцию.

Рассмотрим задачу оптимального планирования производства красок на фабрике. Фабрика выпускает два типа красок: для внутренних (I) и наружных

(E) работ. Продукция обоих видов поступает в оптовую продажу. Для произ-

водства красок используются два исходных продукта А и В (табл. 4.1).

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более, чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тон-

ны краски равны: 3000 руб. для краски Е и 2000 руб. для краски I. Какое коли-

чество краски каждого вида должна производить фабрика, чтобы доход от реа-

лизации продукции был максимальным?

Итак, требуется спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются xI – суточ-

ный объем производства краски I и xЕ – суточный объем производства

краски Е.

Суммарная суточная прибыль от производства xI тонн краски I и xЕ тонн краски Е равна z = 3000xЕ + 2000xI . Задача заключается в определении среди всех допустимых значений xI и xЕ таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z.

80