Теория и методология научно-технического творчества

ТЕМА 8. Изучаемые вопросы: Понятие о прикладных методах математической обработки экспериментальных данных; Гистограмма и кривая распределения случайной величины; Статистические характеристики.

Прикладные методы математической обработки экспериментальных данных

Для установления законов формирования переменных нагрузок, действующих на детали автомобиля при его движении с раз личными скоростями по дорогам с разной степенью ровности, не­обходимо найти математические описания связей между характеристиками переменных воздействий на колеса и характеристиками сил, возникающих при этом в трансмиссии и ходовой части автомобиля. Основной характеристикой степени ровности дорожного покрытия является микропрофиль дороги. Следует иметь в виду, что поскольку процесс нагружения деталей автомобиля является случайным, то при его движении по дороге данного микропрофиля запись функции «нагрузка - время» на отрезке дороги любой протяженности в принципе не повторяется. Однако каждая запись данной функции достаточной протяженности мо­жет быть описана при помощи функции распределения.

Если статистические параметры, соответствующие моменту времени t₁ не изменяются со временем и равны параметрам, полу­ченным в момент времени t₂, то тогда процесс будет стационарным и эргодическим (эргодический процесс всегда стационарный, но стационарный процесс может и не быть эргодическим).

Установлено, что для автомобилей одной модели при эксплуа­тации в одинаковых условиях статистические закономерности функции «нагрузка - время» должны быть одинаковыми. При рассмот­рении воздействия заданного микропрофиля дороги в виде случай­ной стационарной функции реакцию динамической системы авто­мобиля тоже следует характеризовать как случайный процесс. Связь между энергетическими спектрами входного воздействия и реакцией системы, т. е. интенсивностью реакции динамической системы на заданный случайный процесс воздействия, выражается через квадрат модуля передаточной функции динамической си­стемы автомобиля.

Приложение теории случайных функций к формированию процессов нагружения деталей при стендовых испытаниях позво­ляет добиться хорошего совпадения по виду и времени разрушения с результатами, полученными во время дорожных испытаний.

На методах математической статистики базируются и современ­ные работы по расчету деталей автомобиля на долговечность.

1. Статистические характеристики

Если исследуемые процессы носят случайный характер, то для их описания применяются основные положения теории вероятностей и матема­тической статистики.

Характеристики материалов и конструкций (нагрузка на колеса автомобиля, величина силы тяги, мгновенный расход топлива и т. п.) являются также случайными величинами, зависящими от множе­ства факторов. Эти характеристики определяют при испытаниях, поэтому результаты испытаний необходимо обрабатывать с помощью методов математической статистики.

Внедрение вероятностных методов исследования в практику расчетов автомобиля дает возможность правильно оценить исследуемые процессы.

Рассмотрим методы теории вероятностей и ма­тематической статистики, получившие распространение при анализе процессов автомобиля при его эксплуатации.

Каждое исследование случайных явлений, выполняемое мето­дами теории вероятностей, прямо или косвенно основывается на экспериментальных данных. Характеристики случайных величин, получаемые из опыта, называются статистическими или выбороч­ными. Если число испытаний велико, то статистические харак­теристики приближенно оценивают вероятностные характеристики. Так, например, при неограниченном числе опытов статистическое среднее приближается к математическому ожиданию.

При исследовании процессов функционирования автомобиля часто получают последовательный ряд величин, ха­рактеризующих внешнюю нагрузку, действующую на данный агрегат, или деталь. Первичная обработка этого экспе­риментального материала обычно состоит в группировке найден­ных значений по достаточно малым интервалам, вычислении сред­них относительных частот (частостей) р₁ для каждого интервала напряжения или нагрузки и графическом представлении резуль­татов в виде гистограмм и кривых распределения.

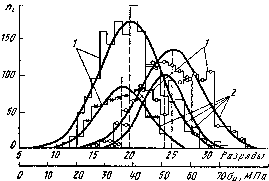
Рис. 25. Распределения напряжений изгиба _и в балке заднего моста грузового автомобиля: 1 – гистограммы; 2- кривые распределения

В качестве примера распределения случайных величин при статистической обработке экспериментальных данных по нагруженности деталей автомобиля на рис. 25 приведены гистограммы распределения напряжений в балке заднего моста автомобиля. По оси абсцисс отложены напряжения изгиба _и, а по оси ординат - частота их повторения п₁ в принятом интервале (разряде).

При увеличении объема выборки (при п  ∞) и уменьшении интервала (увеличении количества разрядов напряжений) гисто­грамма 1 будет более приближаться к некоторой кривой 2. Если при этом перестроить гистограмму, в относительных величинах, то кривая 2 будет представлять собой функцию распределения ве­роятностей появления нагруженности детали в данных условиях эксплуатации.

На рис. 26 приведена гистограмма 1 и кривая рас­пределения 2 напряжений τ в полуоси автомобиля. Полученная таким образом функция дает информацию о распределении на­пряжений в данной детали.

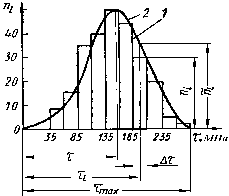
Рис. 26. Распределения напря­жений в полуоси автомобиля:

1 — гистограмма; 2 — кривая рас­пределения; τ — приращение на­пряжения (диапазон измерения на­пряжения); — среднее значение (выборочное математическое ожи­дание) напряжения

При статистической обработке информации о нестационарных случайных процессах нагружения пользуются следующими услов­ными обозначениями:

X - случайная величина (например, касательное напряжение τ в полуосях автомобиля, см. рис. 26);

x_i - наблюдаемое значение случайной величины (например, значение напряжений τ_i , в данный момент времени) или величина, принятая для обозначения разряда;

п_i - частота (разрядная частота), т. е. число случаев, в которых на­блюдалось значение разрядной вели­чины x_i ;

п — объем ряда, т. е. сумма всех частот ряда распределения:

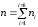(26)

Р_i — частость или относительная частота, т. е. отношение частоты к объему ряда:

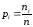(26)

При анализе экспериментальных данных, исследовании распределения случайных величин и в ряде других случаев приходится использовать статистические характеристики.

К статистическим характеристикам прежде всего следует от­нести среднее арифметическое значение случай­ной величины. Среднее арифметическое представляет собой аб­сциссу центра тяжести площади графика распределения. По имею­щимся экспериментальным данным среднее арифметическое мо­жет быть вычислено по следующей формуле:

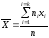(28)

Основными характеристиками рассеяния случайных величин являются дисперсии этих величин, которые определяют по вы­ражению:

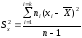(29)

За меру рассеяния принимают также среднее квадратическое отклонение (или стандарт), равное квадратному корню из дис­персии, взятому с положительным знаком:

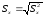(30)

Если нужно оценить степень рассеяния ряда при помощи без­размерной характеристики, то в этом случае используют коэффициент вариации, определяемый как отношение среднего квадратического отклонения к среднему арифметическому:

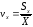(31)

Применение этого коэффициента целесообразно в тех случаях, когда средние значения нескольких сравниваемых распределе­ний значительно отличаются одно от другого. Коэффициент вариа­ции чаще всего выражают в процентах, для этого значения, вы­численные по формуле (31), умножают на 100. Коэффициент вариации широко применяется в теории надежности конст­рукций.

Для анализа асимметричности, а также плосковершинности кривой распределения необходимо знать величины асимметрии S_k и эксцесса Е_k. Они могут быть вычислены по следующим формулам:

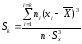; (32)

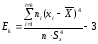(33)

На рис. 27, а) показано два асимметричных распределения: одно из них (кривая 1) имеет положительную асимметрию (S_k > 0), другое (кривая 2) - отрицательную (S_k < 0).

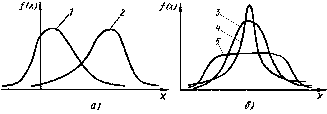
Рис. 27. Влияние асимметрии и эксцесса на положение кривой распре­деления

На рис. 27, б) изображена плотность нормального распределе­ния, когда эксцесс равен нулю (Е_k = 0, кривая 3), плотность рас­пределения с положительным эксцессом (Е_k > 0, кривая 4), при этом кривая 4 имеет более островершинную форму, чем кри­вая 3, плотность распределения с отрицательным эксцессом (Е_k < 0, кривая 5), при этом кривая 5 имеет более плосковершин­ную форму, чем кривая 3.