
3 лаба информатика 1 курс скайлаб / Лаб.3 / Лаб 3 SciLab v1
.pdf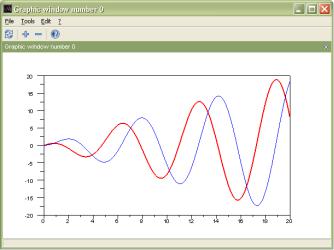
-->plot(x,y)
В результате получим окно с графиками, изображенное на рис.2.
Рис. 2 Графическое окно
Для построение графика функций двух переменных необходимо сначала сформировать матрицу значений функции, например так:
-->x=-5:0.5:5; -->y=-5:0.5:5;
-->z=10*(exp((-x^2)/20))'*(exp((-y.^2)/20));
а затем с помощью команды plot3d(x,y,z) построить график (рис.3).
11

Рис. 3 График функции двух переменных
Сценарии. Файл сценария --- это список команд SciLab, сохраненный на диске. Для удобства работы со сценариями в комплекте SciLab имеется текстовый редактор (пункт меню Editor). Сценария сохраняются в виде файлов с расширением sce. Загрузить сценарий на исполнение можно двумя способами:
–с помощью пункта меню Execute->Load into SciLab встроенного радактора
–с помощью команды exec('Путь к файлу сценария'). ЦЕЛЕСООБРАЗНО ИСПОЛЬЗОВАТЬ СЦЕНАРИИ ПРИ
ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ!!!
Функции. Система SciLab предоставляет несколько способов определения новых функций. Первый из них --- ис-
пользование команды deff: deff('[Рез1,Рез2,...]=ИмяФункции(Арг1,Арг2,...)',
'Тело функции; Рез1=выражение; Рез2=выражение;...')
12
Для того, чтобы использовать функции в будущем целесообразно размещать их в отдельных файлах с расширением sci (можно по нескольку функций в одном файле). В этом случае каждую функцию необходимо оформлять следующим образом:
function [Рез1,Рез2,...]=ИмяФункции(Арг1,Арг2,...) Тело функции...
Рез1=выражение; Рез2=выражение;...
...
endfunction
Перед использованием функции должны быть загружены в систему SciLab с помощью одной из команд
-->exec('Путь к файлу функции'), -->getf('Путь к файлу функции').
Дифференцирование. Пакет программ SciLab имеет возможности численного дифференцирования несколькими способами.
1 способ. Если функция задана таблицей своих значений (т.е. вычислен вектор y значений функции для некоторого вектора x), то для нахождения первого дифференциала используют функцию
-->dy1=diff(y)
а для нахождения n-го дифференциала
-->dyn=diff(y,n).
После нахождения дифференциалов рассчитывают производную по формуле
y ' =1h dy1− dy22 dy33 − dy44 dy55 −...
13
Например, вычислим значение производной функции f x = x 2 3 5x в точке x=1. Введём функцию
-->function y=f(x), y=(x+2)^3+5*x, endfunction;
Определим вектор x и вычислим вектор y=f(x):
--> h=0.1
--> x=0:h:3 // 31 компонент вектора --> y=f(x)
Вычислим дифференциалы первого, второго и третьего порядка:
--> dy1=diff(y,1); --> dy2=diff(y,2); --> dy3=diff(y,3);
Заметим, что размерность вектора dy1 на единицу меньше размерности векторов x и y, то есть составляет 30 компонент. Аналогично размерность вектора dy2 на 1 меньше размерности dy (29 компонент), а размерность dy3 на 1 меньше размер-
ности вектора dy2 (28 элементов). Рассчитываем вектор зна-
чений первой производной, учитывая три первых дифференциала
--> for k=1:28, z(k)=(dy1(k)-dy2(k)/2+dy3(k)/3)/0.1, end
Значение х=1 является одиннадцатым компонентом вектора x. Поэтому выведем на экран значение z(11):
--> disp(z(11)) 32.
Это и есть искомое значение производной.
2 способ. С помощью команды
--> g=numdiff(fun,x),
где первый аргумент — имя дифференцируемой функции, второй — значение переменной х, по которой происходит
14
дифференцирование. Например, вычислим значение производной функции f x = x 2 3 5x в точке x=1
-->function f=my(x), f=(x+2)^3+5*x, endfunction; -->numdiff(my,1)
ans = 32. -->x=1;3*(x+2)^2+5 ans = 32.
В следующем примере вычислим значение первой производной в нескольких точках m=[0:3]
-->v=0:3; |
|
|
|
-->numdiff(my,v) |
|
||
ans = |
|
|
|
17. |
0. |
0. |
0. |
0. |
32. |
0. |
0. |
0.0. 52.999999 0.
0.0. 0. 80.000002
-->function f1=my1(x), f1=3*(x+2)^2+5, endfunction; -->my1(v)
ans = 17. 32. 53. 80.
15
Практическое задание.
В вашем варианте дана функция f t и точка x0 .
1.Разложите заданную функцию f t в ряд Тейлора в окрестности точки x0 . Найдите 10 первых коэффициентов ряда.
2.Напишите функцию, реализующую вычисление приближенного значения заданной вам функции суммированием первых n членов ряда Тейлора.
3.Постройте на одном графике заданную функцию вместе с приближенной.
4.Вычислите ошибку представления заданной функции своими приближениями. Постройте на отдельном графике ошибку в зависимости от х.
Варианты
№ |
Функция f(t) |
Точка x0 |
1 |
f x =exp −x2 |
0 |
2 |
f x =cos x |
1 |
3 |
f x =x8 3x2−2 |
2 |
4 |
f x =exp −x cos 5x |
3 |
5 |
f x =sin x2 |
π |
6 |
f x =tg x |
0 |
7 |
f x =ctg x |
π /2 |
8 |
f x =1−2cos x |
0 |
9 |
f x =8x tg x |
0 |
10 |
f x =x exp −x2 |
0 |
16
|
11 |
f x =sin x |
|
0 |
|
|
|
|
|
|
|
x |
|
|
|
12 |
f x =sin2 x cos2 2x |
|
1 |
|
13 |
f x =exp −x2 x |
|
|
|
14 |
f x =sin2 x2 |
|
2 |
|
15 |
f x =cos x exp −x2 |
|
π |
|
|
Пример выполнения работы. |
||
Пусть дана функция f x =x2 exp −x2 |
и точка x0=1. |
|||
1.Создадим файл сценария test.sce. Все описываемые далее команды будем писать в файле сценария и загружать его на выполнение.
2.Определим функцию
function y=f(x), y=(x^2)*exp(-x^2), endfunction;
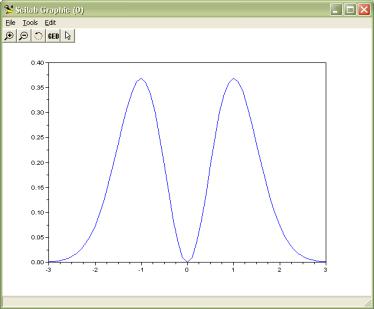
и построим ее график t=-5:0.1:5;
ff=f(t);
plot(t,ff)
3.Для нахождения производных введем дискретизацию некоторой окрестности исходной точки x0. При этом точка х0 должна располагаться не посередине выбранной окрестности, а ближе к ее левому краю.
x=0:0.1:5
Заметим, что при таком выборе дискретизации исходная точка x0 имеет номер 11, то есть х(11)=х0.
4.Вычисляем значения функции в узлах дискретизации y=f(x);
5.Находим значения первой производной в узлах дискретизации
dy1=diff(y,1);
dy2=diff(y,2);
dy3=diff(y,3); for k=1:28
z(k)=(dy1(k)-dy2(k)/2+dy3(k)/3)/0.1; end
disp(z(11))
6.Вычисляем значения второй производной dz1=diff(z,1);
dz2=diff(z,2);
dz3=diff(z,3); for k=1:25
w(k)=(dz1(k)-dz2(k)/2+dz3(k)/3)/0.1; end
disp(w(11))
18
7.Вычисляем значения третьей производной dw1=diff(w,1);
dw2=diff(w,2);
dw3=diff(w,3); for k=1:22
v(k)=(dw1(k)-dw2(k)/2+dw3(k)/3)/0.1; end
disp(v(11))
8.Вычисляем значения четвертой производной dv1=diff(v,1);
dv2=diff(v,2);
dv3=diff(v,3); for k=1:19
q(k)=(dv1(k)-dv2(k)/2+dv3(k)/3)/0.1; end
disp(q(11))
9.Формируем ряд Тейлора x0=x(11);
A=y(11);
B=z(11);
C=w(11)/2;
D=v(11)/6;
E=q(11)/24;
function y=g(x), y=A+B*(x-x0)+C*(x-x0)^2+ D*(x-x0)^3+E*(x-x0)^4 , endfunction;
19

10. Строим график функции g(x) gg=g(t);
plot(t,gg)
Получаем
11.Введем функцию ошибки приближения рядом Тейлора function e=err(x), e=abs(f(x)-g(x)), endfunction;
20
