
Лекция 13.
Пятый постулат Евклида, попытки его доказательства. Эквиваленты пятого постулата. Аксиоматика Гильберта. Следствия из аксиом Гильберта. Абсолютная геометрия. Аксиоматика Вейля.
В абсолютной геометрии (без использования пятого постулата) можно доказать: признаки равенства треугольника; в равнобедренном треугольнике углы при основании равны; теорему о внешнем угле треугольника: каждый из внешних углов треугольника больше любого внутреннего, с ним не смежного.
Д оказательство
(по Евклиду)
оказательство
(по Евклиду)
1.
![]() .
Тогда треугольник
.
Тогда треугольник![]() равняется треугольнику
равняется треугольнику![]() (по двум сторонам и углу между ними),
следовательно,
(по двум сторонам и углу между ними),
следовательно,![]() .
Но угол
.
Но угол![]() составляет часть внешнего угла при
вершине
составляет часть внешнего угла при
вершине![]() .
Значит, теорема доказана.
.
Значит, теорема доказана.
Последний момент
(что угол
![]() составляет
часть внешнего угла) устанавливается
из наглядности чертежа, т.к. аксиомы
Евклида не дают возможности точно
обосновать понятия «между», «внутри»
и т.д. Кроме того, в доказательстве
использовалось понятие равенства
треугольников, которое не обосновано,
т.к. не определено движение у Евклида.
Таким образом, приведенные рассуждения
существенно подкрепляются наглядностью
чертежа.
составляет
часть внешнего угла) устанавливается
из наглядности чертежа, т.к. аксиомы
Евклида не дают возможности точно
обосновать понятия «между», «внутри»
и т.д. Кроме того, в доказательстве
использовалось понятие равенства
треугольников, которое не обосновано,
т.к. не определено движение у Евклида.
Таким образом, приведенные рассуждения
существенно подкрепляются наглядностью
чертежа.
Пользуясь теоремой о внешнем угле треугольника без помощи пятого постулата легко доказывается следующая лемма: если при пересечении двух прямых секущей накрест лежащие углы (или соответственные углы) равны, то прямые не пересекаются.
Доказательство.
П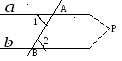 усть
при пересечении прямых
усть
при пересечении прямых![]() и
и![]() секущей АВ накрест лежащие углы равны
(например,
секущей АВ накрест лежащие углы равны
(например,![]() ).
Допустим, что прямые
).
Допустим, что прямые![]() и
и![]() пересекаются в некоторой точке
пересекаются в некоторой точке![]() ,
то получим треугольник
,
то получим треугольник![]() ,
у которого один из углов при вершине
,
у которого один из углов при вершине![]() или
или![]() равен внешнему, что противоречит теореме
о внешнем угле. Второе утверждение
следует непосредственно из доказанного.
равен внешнему, что противоречит теореме
о внешнем угле. Второе утверждение
следует непосредственно из доказанного.
Пользуясь данной
леммой, легко доказывается (без
использования пятого постулата), что
через каждую точку М, не лежащую на
прямой
![]() ,
проходит прямая, параллельная прямой
,
проходит прямая, параллельная прямой![]() .
.
Возникает вопрос:
сколько же прямых, параллельных прямой
![]() ,
проходит через точкуМ.
Ответ на этот вопрос дает следующая
теорема: если
имеет место пятый постулат, то через
каждую точку М, не лежащую на прямой
,
проходит через точкуМ.
Ответ на этот вопрос дает следующая
теорема: если
имеет место пятый постулат, то через
каждую точку М, не лежащую на прямой
![]() ,
проходит только одна прямая, параллельная
прямой
,
проходит только одна прямая, параллельная
прямой![]() .
.
Доказательство:
П
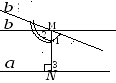 роведем
прямую
роведем
прямую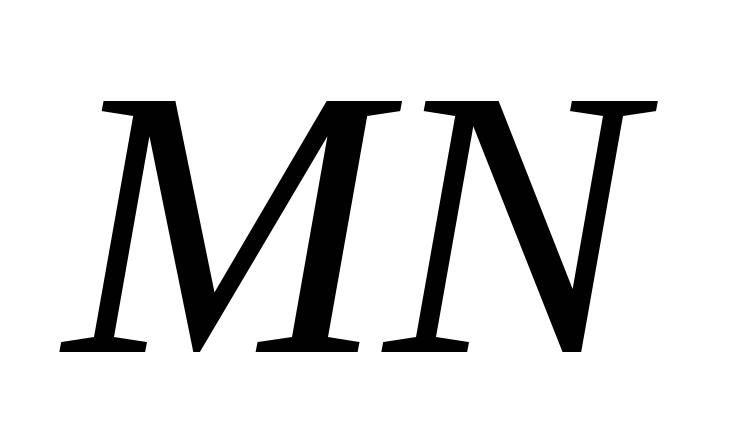 ,
перпендикулярную к прямой
,
перпендикулярную к прямой ,
, и прямую
и прямую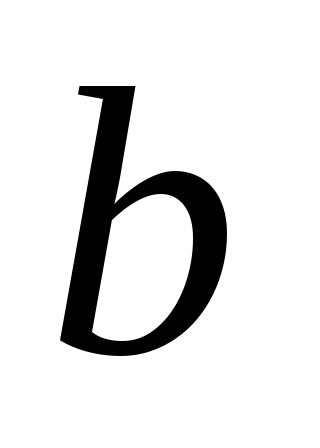 ,
проходящую через точку
,
проходящую через точку перпендикулярно
к прямой
перпендикулярно
к прямой .
Тогда прямые
.
Тогда прямые и
и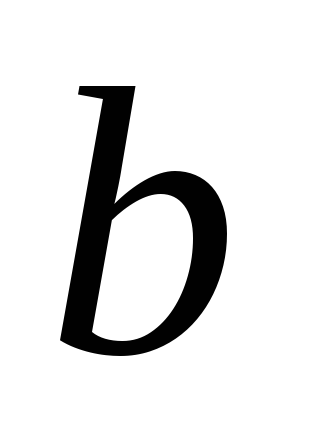 параллельны.
параллельны.Проведем через точку
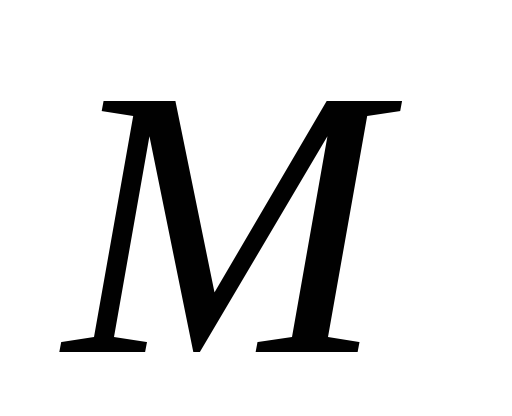 произвольную
прямую
произвольную
прямую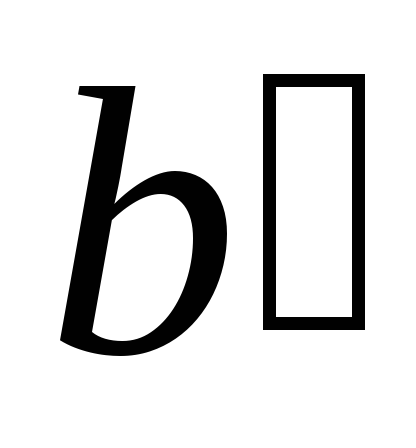 ,
отличную от прямой
,
отличную от прямой .
Один из смежных углов (1 или 2) острый
(пусть
.
Один из смежных углов (1 или 2) острый
(пусть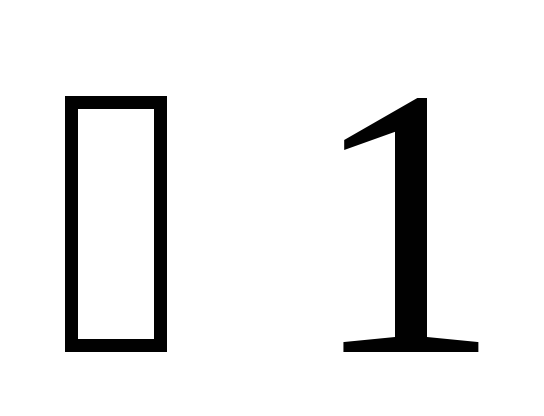 ).
При пересечении прямых
).
При пересечении прямых и
и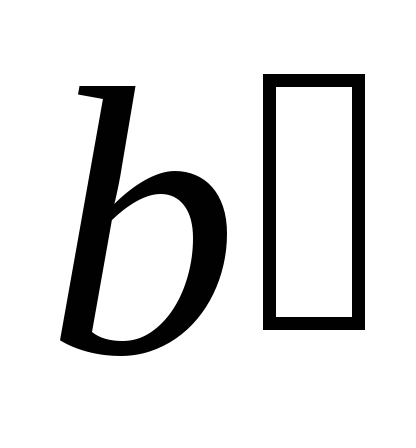 с
прямой
с
прямой получаем
внутренние односторонние углы:
получаем
внутренние односторонние углы: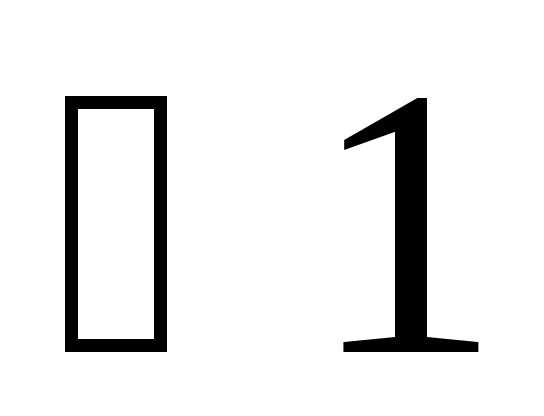 и
и ,
сумма которых меньше двух прямых углов,
значит по пятому постулату прямые
,
сумма которых меньше двух прямых углов,
значит по пятому постулату прямые и
и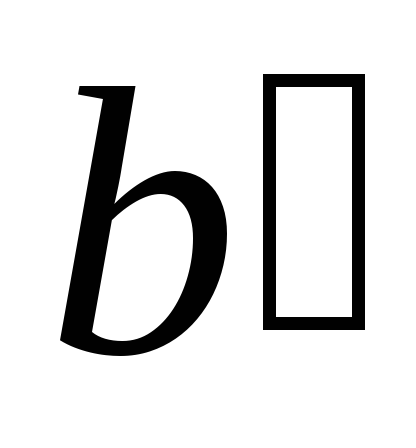 пересекаются.
пересекаются.
Д окажем
обратную теорему:если
принять, что через точку, не лежащую на
данной прямой, проходит одна прямая,
параллельная данной, то справедлив
пятый постулат.
окажем
обратную теорему:если
принять, что через точку, не лежащую на
данной прямой, проходит одна прямая,
параллельная данной, то справедлив
пятый постулат.
Доказательство.
Пусть при пересечении прямых
 и
и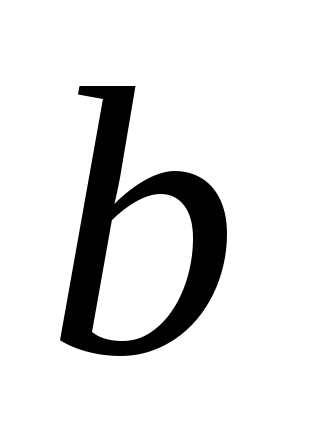 секущей
секущей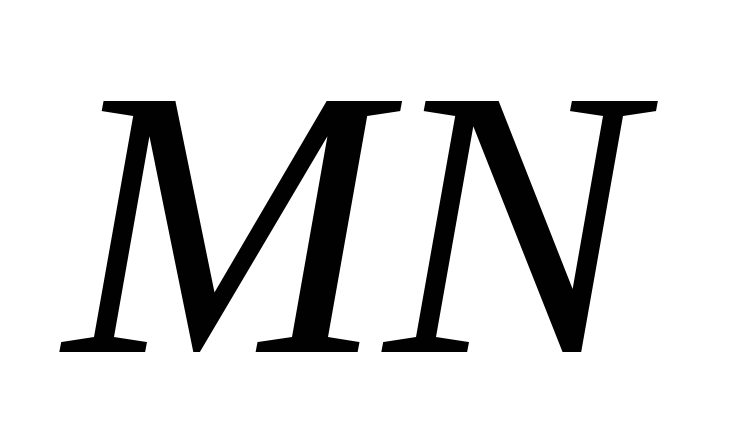 образованы
внутренние односторонние углы
образованы
внутренние односторонние углы и
и так, что
так, что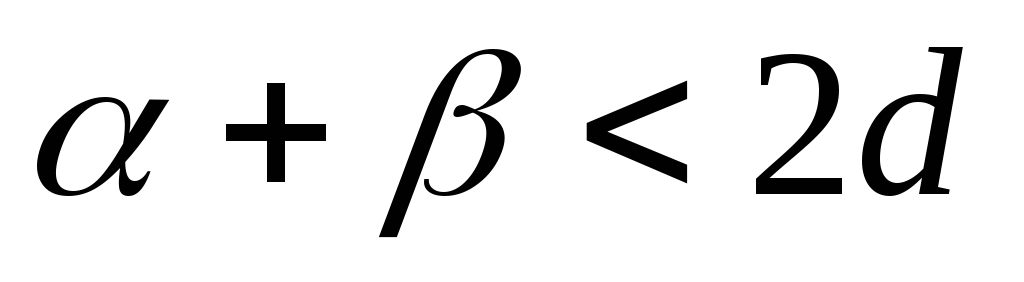 ,
где
,
где -
мера прямого угла. Докажем, что прямые
-
мера прямого угла. Докажем, что прямые и
и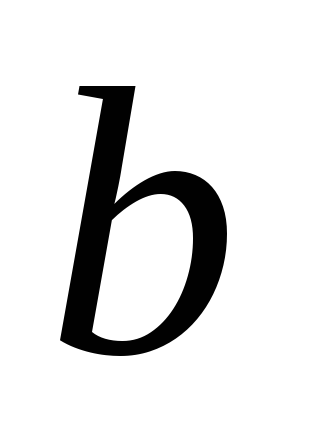 пересекаются в некоторой точке, лежащей
в полуплоскости, в которой лежат углы
пересекаются в некоторой точке, лежащей
в полуплоскости, в которой лежат углы и
и .
.Обозначим через
 угол смежный с углом
угол смежный с углом и накрест лежащий с углом
и накрест лежащий с углом .
Так как
.
Так как ,
то из 1) следует, что
,
то из 1) следует, что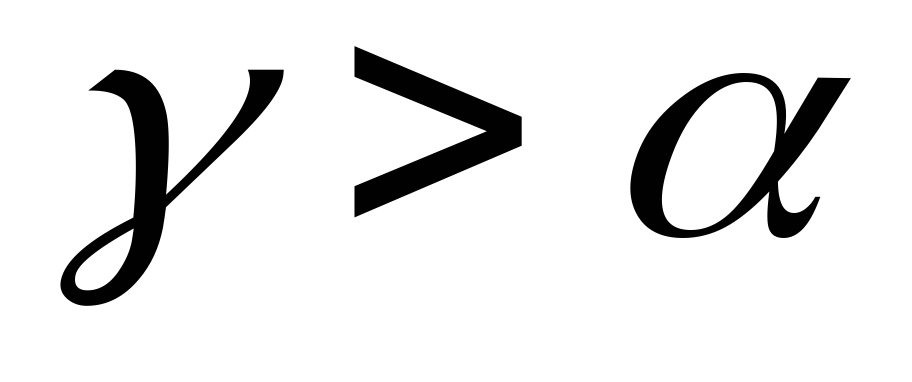 .
.Отложим от луча
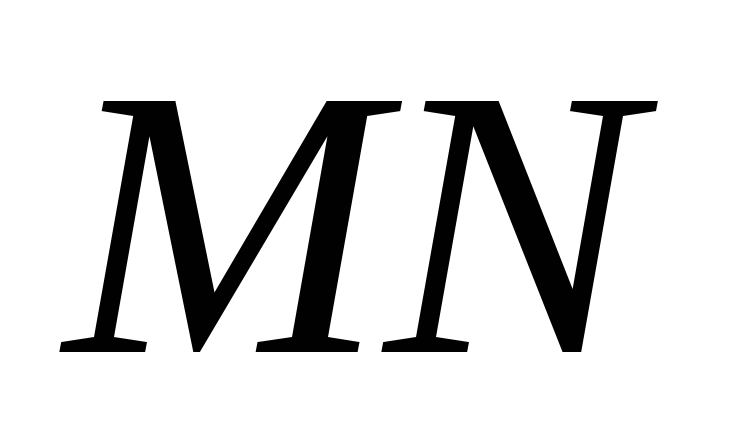 угол
угол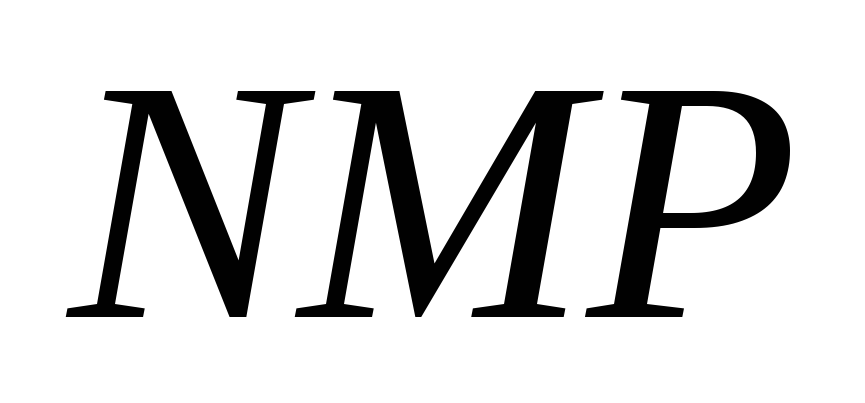 ,
равный углу
,
равный углу ,
так, чтобы
,
так, чтобы и
и были
накрест лежащими углами при пересечении
прямых
были
накрест лежащими углами при пересечении
прямых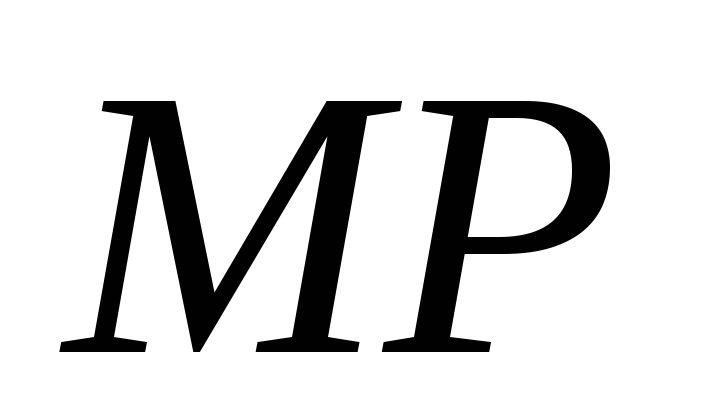 и
и прямой
прямой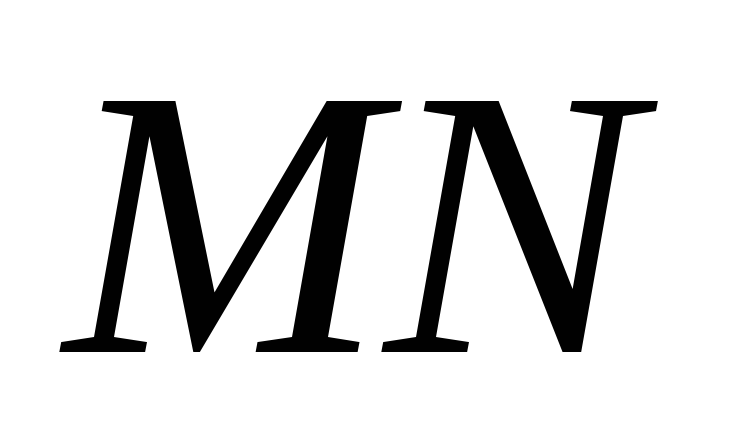 .
По лемме прямые
.
По лемме прямые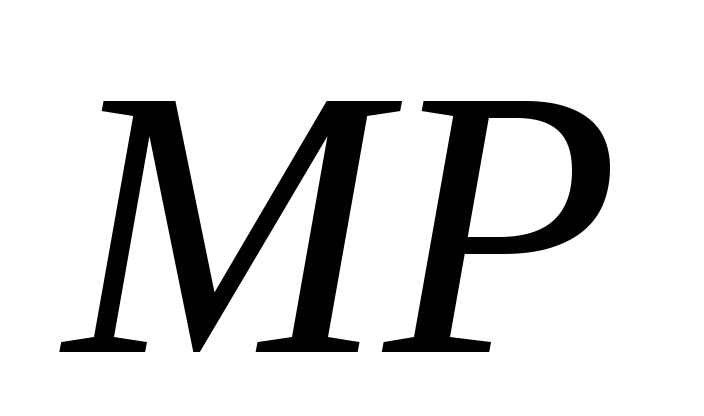 и
и параллельны. В силу неравенства
параллельны. В силу неравенства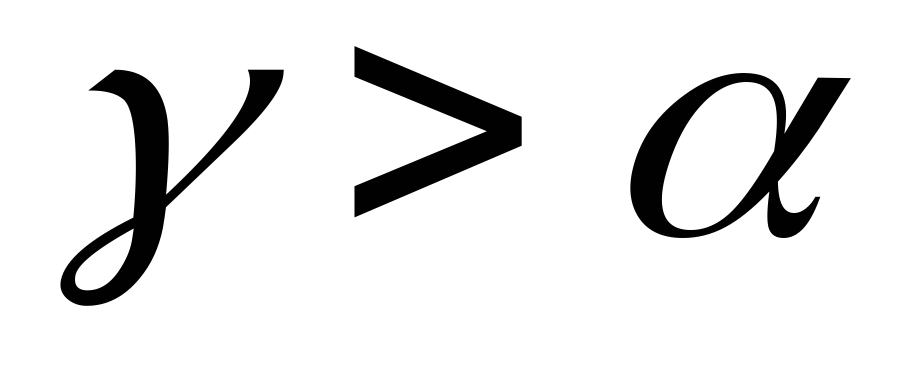 прямые
прямые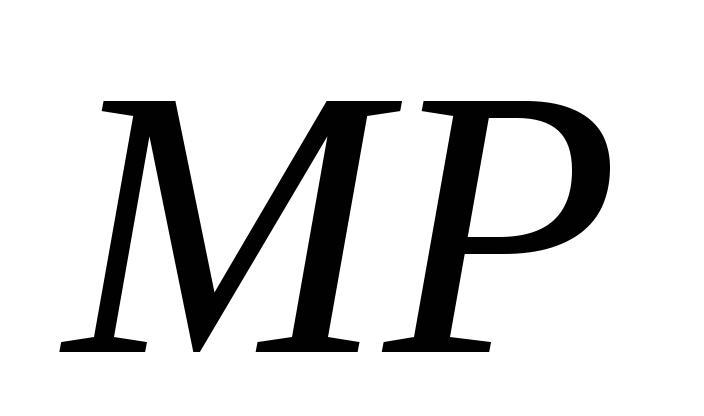 и
и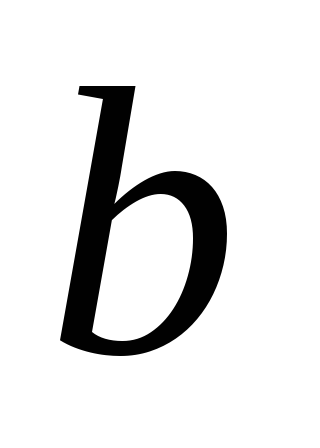 не совпадают. Так как через точку
не совпадают. Так как через точку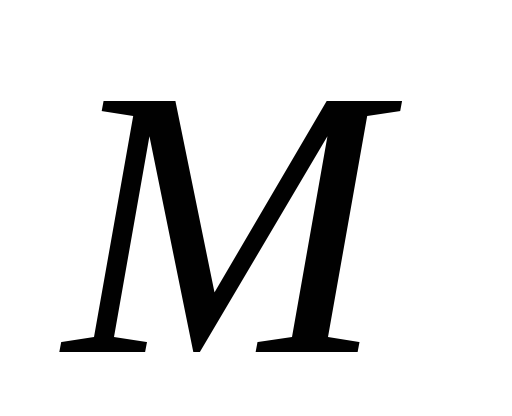 проходит
только одна прямая, параллельная прямой
проходит
только одна прямая, параллельная прямой ,
то прямые
,
то прямые и
и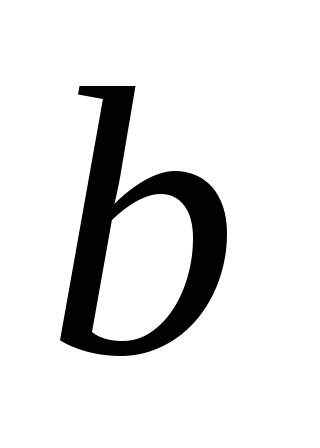 пересекаются
в некоторой точке
пересекаются
в некоторой точке .
.Если предположить, что точка
 лежит
в той полуплоскости, в которой лежит
угол
лежит
в той полуплоскости, в которой лежит
угол ,
то в силу неравенства
,
то в силу неравенства придем к противоречию с теоремой о
внешнем угле треугольника. Таким
образом,
придем к противоречию с теоремой о
внешнем угле треугольника. Таким
образом, -
точка той полуплоскости, в которой
лежат углы
-
точка той полуплоскости, в которой
лежат углы и
и .
.
Итак, пятый постулат эквивалентен (равносилен) так называемой аксиоме параллельности прямых: через точку, не лежащую на данной прямой, проходит не более чем одна прямая, параллельная данной.
Итак, 5 постулату
(если две
прямые при пересечении с третьей образуют
с одной стороны внутренние односторонние
углы, сумма которых меньше
![]() ,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(
,
то эти прямые пересекаются при их
достаточном продолжении с этой стороны.
(![]() )в Евклидовой
геометрии отводится особое место.
)в Евклидовой
геометрии отводится особое место.
На нем основана теория параллельных прямых, подобие фигур, теорема о сумме углов в треугольнике, теорема о сумме углов выпуклых многоугольников, тригонометрия, теория площадей и объемов. Попытки доказательства пятого постулата привели к признаку параллельности прямых, аксиом существования параллельной прямой. Пятый постулат также эквивалентен (равносилен) следующим утверждениям.
Сумма углов каждого треугольника равна двум прямым;
Существует хотя бы один треугольник, сумма углов которого равна 2d (d- прямой угол);
существует прямоугольник;
Существует пара треугольников
 и
и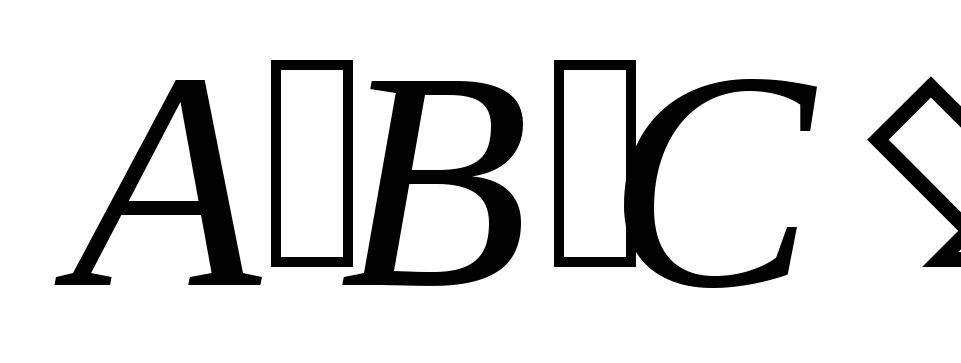 с равными углами;
с равными углами;Теорема Пифагора.
Со времен Евклида и до конца 19 века было множество попыток доказать 5-ый постулат (О.Хойям 1048-1023 г., Лежандр – 1750-1833 г и др.). Обычно автор доказательства незаметно для себя опирался на некоторое допущение, которое оказывалось еще одним эквивалентов 5-го постуоата. Попытки были бесплодными, но был получен ряд верных результатов, наиболее четкое доказательство которых было дано Лежандром.
Со времен Евклида также не прекращались попытки уточнять основные положения геометрии. Однако на протяжении многих веков к обоснованию геометрии никто не прибавил ничего принципиально нового сверх того, что уже было сделано Евклидом. Строгость евклидовых доказательств до 19 века казалась достаточной. Только в конце 19 века оформились воззрения на принципы логического построения геометрии.
В 1899 году вышла в свет книга Д. Гильберта «Основания геометрии». В ней впервые был дан список аксиом, достаточный для логического построения евклидовой геометрии. Полные списки аксиом евклидовой геометрии составлялись и до Гильберта, но не такие совершенные.
По Гильберту, база
структуры евклидова пространства
состоит из трех множеств:
![]() .
.![]() - множество точек,
- множество точек,![]() - множество прямых,
- множество прямых,![]() - множество плоскостей.
- множество плоскостей.
На этих множествах заданы 3 отношения: бинарное «принадлежит»; тернарное «лежит между»; бинарное «равно», которые удовлетворяют 20 аксиомам, разбитым на пять групп.
