Вопросы для самопроверки

1 Как найти распределение функции по известному распределению дискретного и непрерывного аргумента?

2. Приведите формулы для нахождения математического ожидания функции случайного аргумента.

3 Как найти распределение функции двух случайных аргументов?

4 Охарактеризуйте распределение «хи квадрат», Стьюдента, Фишера-Снедекора.

Тема 7. Система двух случайных величин

Цель изучения – ознакомиться с двумерной случайной величины.

Данная тема включает в себя:

- закон распределения дискретной двумерной случайной величины;

- функция распределения вероятностей и плотность совместного распределения вероятностей непрерывной двумерной случайной величины;

- условные законы распределения вероятностей составляющих дискретной двумерной случайной величины;

- отыскание плотностей и условных законов распределения составляющих непрерывной двумерной случайной величины;

- числовые характеристики непрерывной системы двух случайных величин.

Контрольные задачи

1Задана двумерная дискретная случайная величина:

X Y	2	4
0	0,1	0,3
5	0,2	0,15
10	0,15	0,1

Найти законы распределения составляющих случайных величин.

2 Задана двумерная дискретная случайная величина:

X Y	0	5	20
0	0,15	0,2	0,10
10	0,10	0,3	0,15

Найти математическое ожидание и дисперсию составляющих случайных величин X и Y.

3 Задана функция распределения двумерной случайной величины

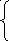1-3^-х-3^-у+3^-х-у при х ≥ 0, у ≥ 0,

0 при х < 0, у < 0.

Найти двумерную плотность вероятности системы (X, Y).

4 Функция распределения случайной двумерной величины задана в задании 3. Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми х = 0, х = 2,у= 1, у = 5.

5 Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми х=1, х=2, у=3, у=5, если известна функция распределения:

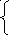1-2^-х-2^-у+2^-х-у при х ≥ 0, у ≥ 0,

0 при х < 0, у < 0.

6 Задана функция распределения двумерной случайной величины:

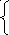(1-е^-4х)(1-е^-2у) при х ≥ 0, у ≥ 0,

0 при х < 0, у < 0.

Найти двумерную плотность вероятности системы (X, Y).

7 Распределение 100 студентов по количеству пропущенных часов занятий и экзаменационной оценке представлено в следующей таблице. Найти безусловные и условные законы распределения случайных величин: количества пропущенных часов (X) и экзаменационной оценки (Y).

Количество пропущенных часов	Оценка на экзамене
	2	3	4	5
0	0	5	10	10
4	5	15	20	15
10	10	5	5	0

8 Распределение хозяйств по дозам внесения удобрений и урожайности озимой пшеницы приведено в следующей таблице:

Дозы	Урожайность, ц с 1 га
	до 35	30-35	35-40	Свыше 40
до 1	18	а	5	-
1-2	а	15	20	10
свыше 2	-	а	12	20

Найти безусловные и условные законы распределения случайных величин урожайности (X) и доз внесения удобрений (Y).

9 Система случайных величин (X, Y) подчинена закону распределения с плотностью f(x,y) = a sin (x + y) в квадрате 0 ≤ x ≤ ; 0 ≤ y ≤ и f(x,y) = 0, вне квадрата. Определить: а) коэффициент а; б) М(Х), M(Y); в) Д(Х), Д(У).

10 Дана дискретная двумерная величина (X, Y):

а) б)

Х Y		2		4
10		0,15		0,10
15		0,3		0,05
20		0,15		0,25

Х Y	100	200
0	0,1	0,25
5	0,05	0,2
10	0,1	0,3

Найти: а) условный закон распределения X при условии, что у=20; б) условный закон распределения У при условии, что х=200.

11 Плотность совместного распределения непрерывной двумерной случайной величины f(x,y) = cosx · cosy в квадрате 0 ≤ x ≤ ; 0 ≤ y ≤ и f(x,y)=0 , вне квадрата. Доказать, что составляющие Х и Y независимы.

12 Непрерывная двумерная случайная величина (X, Y) распределена равномерно внутри треугольника с вершинами О (0,0), А (0,6) и В (6,0). Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности составляющих системы.

13 Система случайных величин (X, Y) распределена равномерно внутри квадрата со стороной а, диагонали которого совпадают с осями координат. Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности составляющих системы.

14 Задана плотность совместного распределения непрерывной двумерной случайной величины (X, Y):

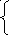36хупри х ≥ 0, у ≥ 0,

0 при х ≤ 0, у ≤ 0.

Найти математические ожидания и дисперсии составляющих.

15. истема случайных величин (X, Y) равномерно распределена в треугольнике, ограниченном прямыми х=0, у=0, х+у=а (а > 0). Определить: а) математические ожидания и дисперсии случайных величин X и Y, б) корреляционный момент.

15. Заданы плотности распределения независимых составляющих непрерывной случайной величины (X, Y):

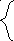0 при х≤ 0, 0 при у ≥ 0,

2е^-2х при х > 0 5е-5у при у > 0.

Найти: а) плотность совместного распределения системы;

б) функцию распределения системы.