
- •Б 2. Б.2. Линейная алгебра
- •080100 Экономика
- •Бакалавр
- •Оглавление
- •Введение
- •Общие методические указания
- •Тема 1 Системы линейных алгебраических уравнений и методы их решения
- •1 Решение систем линейных уравнений методами Крамера и Гаусса
- •Тема 2 Аналитическая геометрия на плоскости
- •2. Уравнение прямой, проходящей через точки м1 (x1;y1) и м2(x2;y2), имеет вид: (2)
- •Тема 3 Векторная алгебра и аналитическая геометрия в пространстве
- •Задания для контрольной работы
- •Литература
- •Дополнительная литература
Тема 3 Векторная алгебра и аналитическая геометрия в пространстве
Задача 4. Даны координаты трех точек: A(3; 0; -5), В,(6; 2; 1),С(12; -12; 3).
Требуется:
1)
записать
векторы
![]() и
и![]() в
системе
орт
и
найти
модули
этих
векторов;
2)
найти
угол
между
векторами
в
системе
орт
и
найти
модули
этих
векторов;
2)
найти
угол
между
векторами
![]() и
и![]() ;
3) составить
уравнение
плоскости,
проходящей
через
точку
С
перепендикулярно вектору
;
3) составить
уравнение
плоскости,
проходящей
через
точку
С
перепендикулярно вектору
![]() .
.
Решение.
1.
Если
даны
точки
М1(х1,
у1,
z1)
и
М2
(х2,
у2,
z2),
то
вектор
![]() через
орты
через
орты
![]() выражается
следующим
образом:
выражается
следующим
образом:
![]() (1)
(1)
Подставляя в эту формулу координаты точек А и В, имеем:
![]()
Подобным
образом
![]()
Модуль
вектора
![]() вычисляется
по
формуле:
вычисляется
по
формуле:
![]() (2)
(2)
Подставляя
в
формулу
(2)
найденные
ранее
координаты
векторов![]() и
и![]() ,
находим
их
модули:
,
находим
их
модули:
![]()
![]()
![]() =17
=17
2.
Косинус
угла
![]() ,
образованного
векторами
,
образованного
векторами
![]() и
и
![]() ,равен
их
скалярному произведению, деленному
на
произведение
их
модулей:
,равен
их
скалярному произведению, деленному
на
произведение
их
модулей:
Cos![]() =
=![]() (3)
(3)
Так как скалярное произведение двух векторов, заданных своими координатами равно сумме попарных произведений одноименных координат, то
![]() *
*
![]() =
3*9+2*(-12)+6*8=51.
=
3*9+2*(-12)+6*8=51.
Применяя
(3), имеем:
сos![]()
![]()
 3.Известно,
что
уравнение
плоскости,
проходящей
через
точку
М0(х0,
у0,
z0)
перпендикулярно
вектору
3.Известно,
что
уравнение
плоскости,
проходящей
через
точку
М0(х0,
у0,
z0)
перпендикулярно
вектору
![]() А;В;
С
имеет
вид
А;В;
С
имеет
вид
A(x – хо) +B(y – уо) + С(z – zо) =0 (4)
По
условию
задачи
искомая
плоскость
проходит
через
точку
С(12;
-
12;
3)
перпендикулярно
вектору
![]()
Подставляя в (4) А=3, В=2, С=6, хо = 12, уо = - 12, zо =3, получим:
3(х – 12)+2(у+12) +6(z – 3) = 0, Зх + 2у + 6z – 30=0 — искомое уравнение плоскости.
Вопросы для самопроверки
1. Какие величины называются скалярными, векторными?
2. Какие векторы навязываются коллинеарными?
3. Какие два вектора называются равными?
4. Как сложить два вектора? Как их вычесть?
5. Как найти координаты вектора по координатам точек его начала и конца?
6. Назовите правила сложения, вычитания векторов, заданных в координатной форме. Как умножить вектор на скаляр?
7. Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.
8. Как найти скалярное произведение двух векторов по их координатам?
9. Напишите формулу для определения угла между двумя векторами.
10.Напишите условия: коллинеарности двух векторов; их перпендикулярности.
11. Напишите общее уравнение плоскости.
12. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
13.Какой вид имеет уравнение плоскости, проходящей через три данные точки?
14.Напишите формулу для определения расстояния от точки до плоскости.
Задания для контрольной работы
Задание 1
В задачах 1-20 решить систему уравнений методами Крамера, Гаусса, записать ее в матричной форме и решить с помощью обратной матрицы.
1.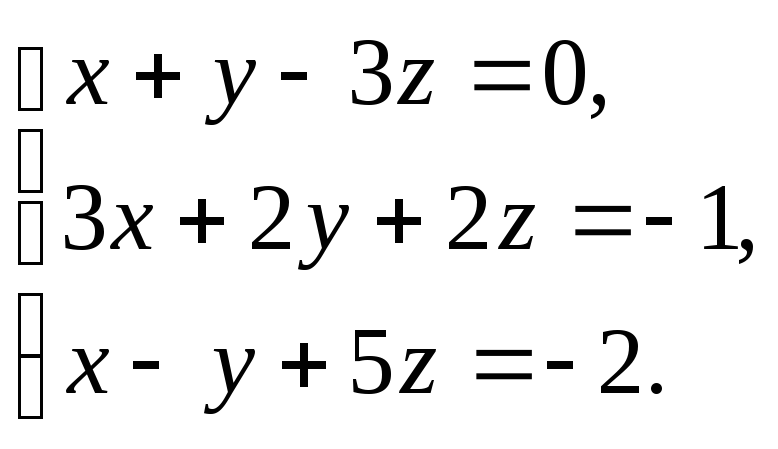 2.
2.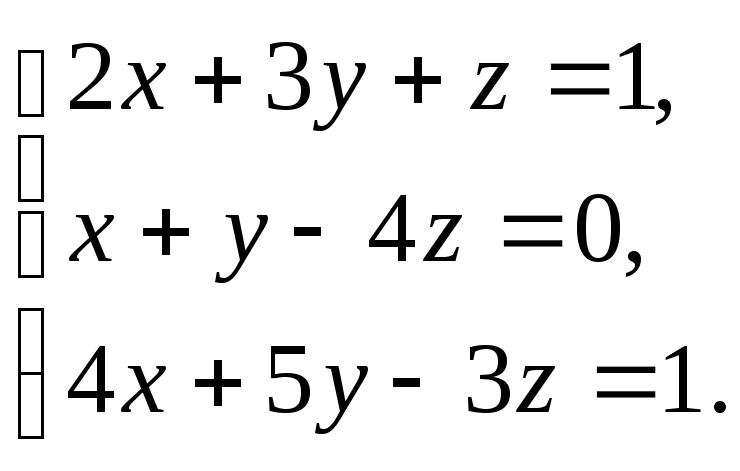
3.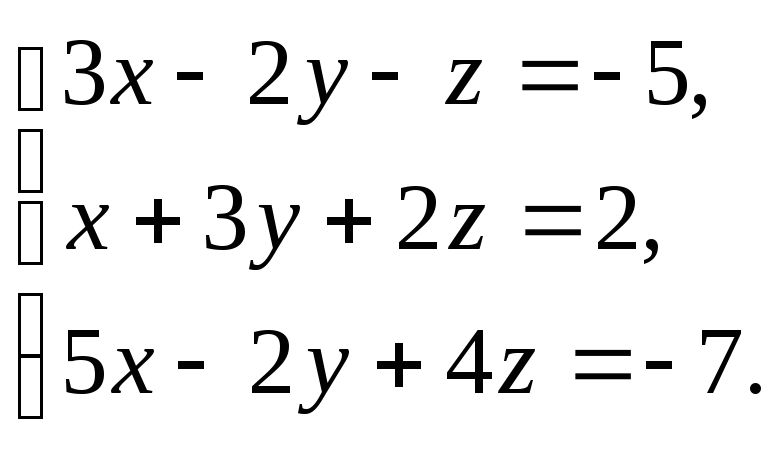 4.
4.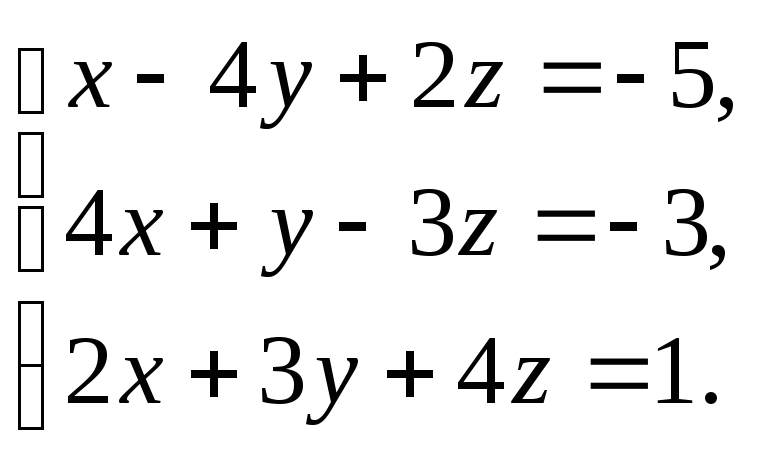
5.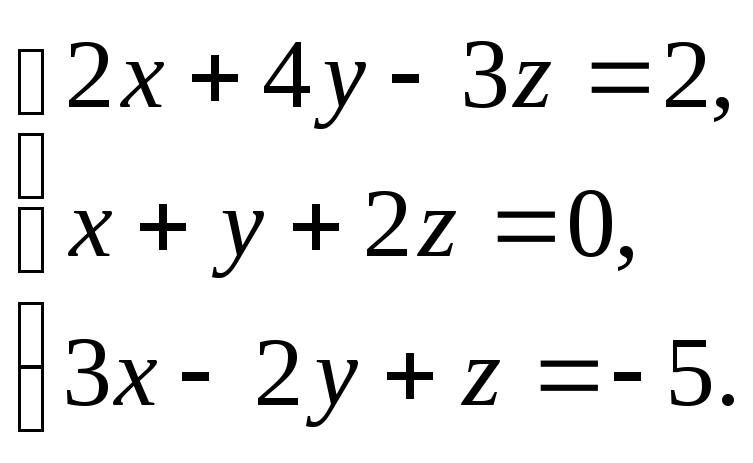 6.
6.
7.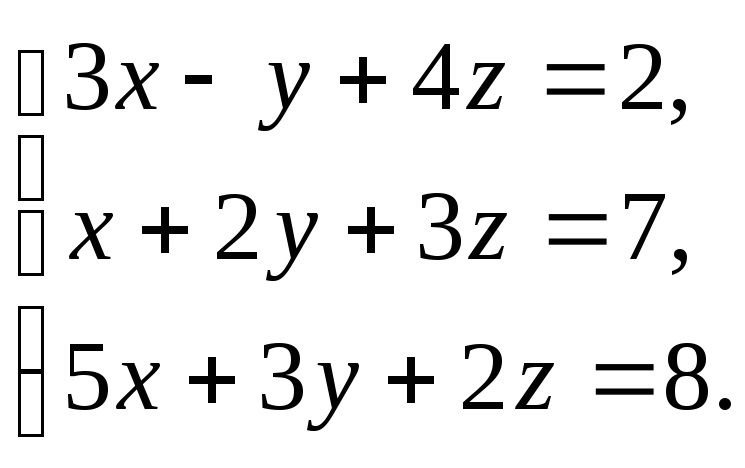 8.
8.
9.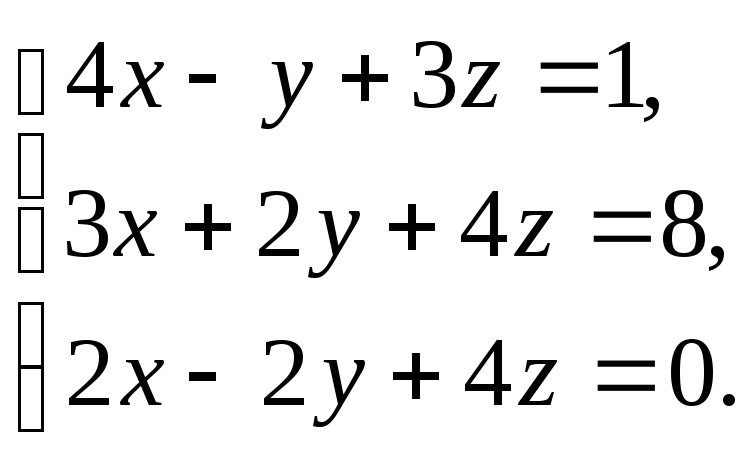 10.
10.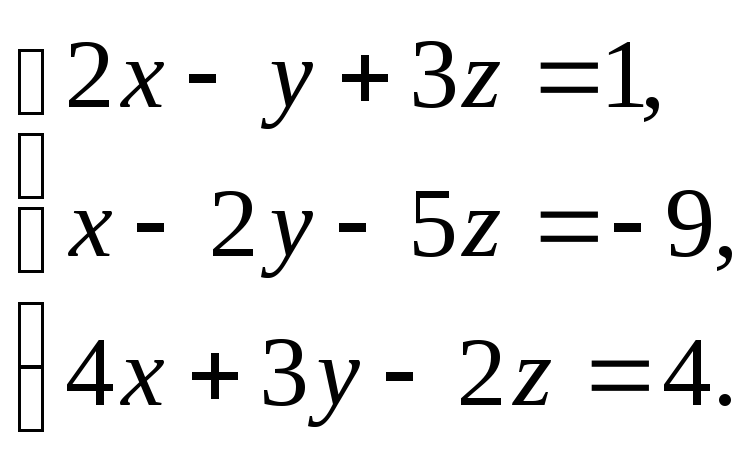
11.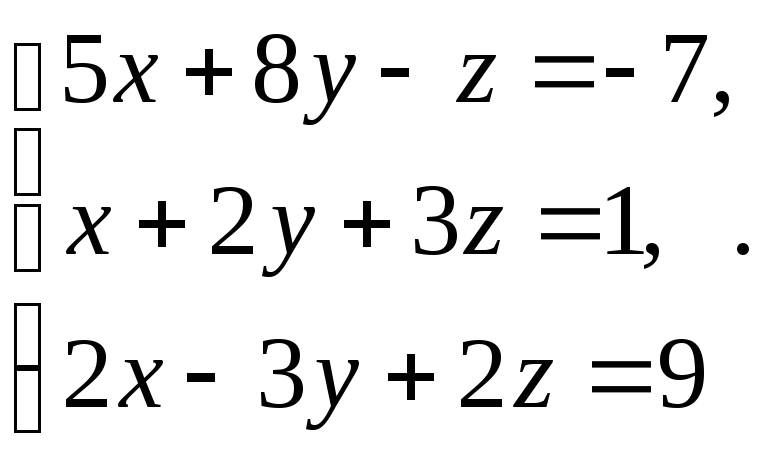 12.
12.
13.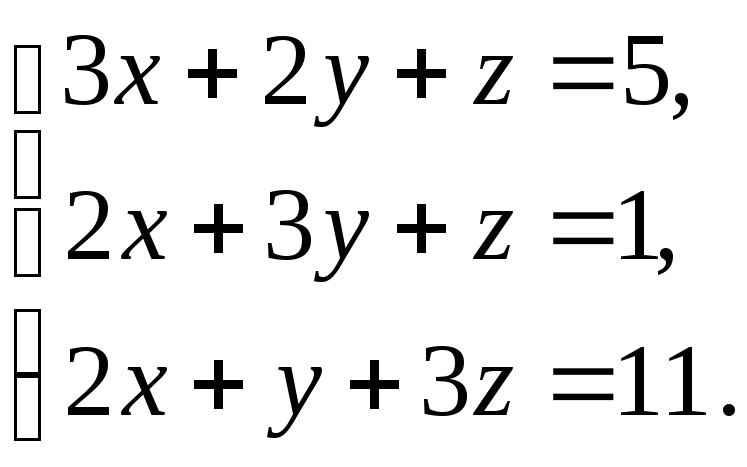 14.
14.
15.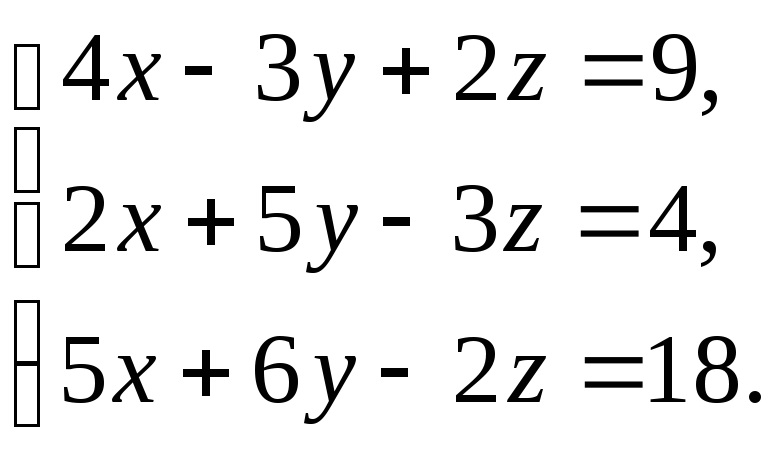 16.
16.
17.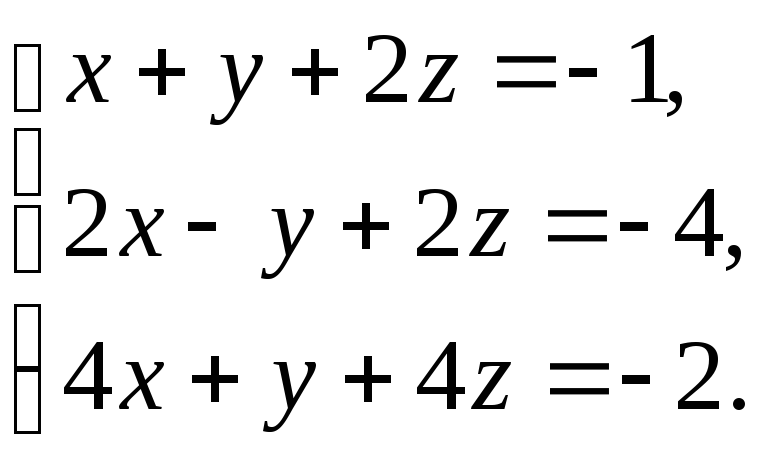 18.
18.
19.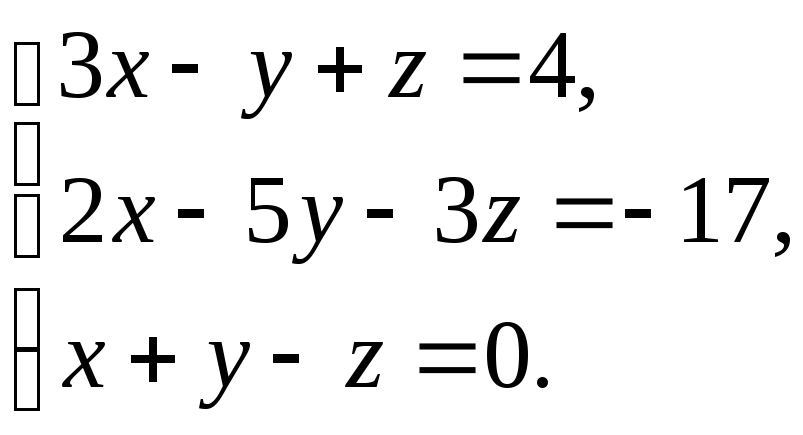 20.
20.
Задание 2
В задачах 1-20 даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А; 4) уравнения высоты СD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник ABC.
1. A (0;-1), B(12;8), C(10;-6). 2. A (-7; 2), B(5; 11), C(3; -3).
3. A (-5;-3), B(7;6), C(5;-8). 4. A (-6;-2), B(6;7), C(4;-7).
5. A (-3;3), B(9;-6), C(7;8). 6. А (-5; 0), B(7; 9), C(5; -5).
7. A (-6;11), B(6;10), C(4;-4). 8. A (-2;-4), B(10;5), C(8;-9).
9. A (-3;0), B(9;9), C(7;-5). 10. A (-9;2), B(3;7), C(1;-7).
11. A (-5;2), B(7;-7), C(5;7). 12. A (-7;5), B(5;-4), C(3;10).
13. A (-7;1), B(5;-8), C(3;6). 14. A (0;3), B(12;-6), C(10;8).
55. A (-8;4), B(4;-5), C(2;9). 16. A (-2;2), B(10;-7), C(8;7).
17. A (1;2), B(13;-7), C(11;7). 18. A (-4;1), B(8;-8), C(6;6).
19. A (-7;-1), B(-5;-10), C(3;4). 20. A (-8;-4), B(4;5), C(2;-9).
Задание 3
В задачах 1-10 составить уравнение линии, для каждой точки которой отношение расстояний до точки А (х1; у1) и до прямой х = а равно числу . Полученное уравнение привести к простейшему виду и построить кривую.
1.
A(4;0), a = 9, ε
=
![]() .
2. A(-8;0), a = - 2,ε
=2.
.
2. A(-8;0), a = - 2,ε
=2.
3. A(4;0), a = 1, ε = 2. 4. A(9;0), a = 4, ε = 1.5.
5.
A(-1;0), a = -4, ε
=
![]() .
6. A(5;0), a =9,ε
=
.
6. A(5;0), a =9,ε
=
![]() .
.
7.
A(-1;0), a = -4, ε
=
![]() 8.
A(4;0), a = 7, ε
=
8.
A(4;0), a = 7, ε
=
![]()
9.
A(3;0),a
= 8, ε =
![]() 10.
A(-4;0),a
= -2, ε =3.
10.
A(-4;0),a
= -2, ε =3.
В задачах 11-20 составить уравнение линии, для каждой точки которой ее расстояние до точки А (х1; у1) равно расстоянию до прямой у = b. Полученное уравнение привести к простейшему виду и построить кривую.
11. А (2;1), b=- 1. 12. A (-2; -2), b= - 4.
13. A (2;-1), b=2. 14. A (2; -1), b=1.
15. A (4; -1), b=1. 16. А (4;1), b=- 1.
17. А (3;1), b=- 1. 18. А (2;1), b=- 2.
19. А (4;1), b=- 2. 20. А (6;1), b=- 1.
Задание 4
В
задачах 1-20 даны координаты точек А, В,
С. Требуется : 1) записать векторы
![]() и
и![]() в системе орт и найти модули этих
векторов; 2) найти угол между векторами
в системе орт и найти модули этих
векторов; 2) найти угол между векторами![]() и
и![]() ;
3) составить уравнение плоскости,
проходящей через точку С перпендикулярно
вектору
;
3) составить уравнение плоскости,
проходящей через точку С перпендикулярно
вектору![]() .
.
1. А(7;-4;1), B(12;-3;1), C(10;1;5). 2. А(0;-3;3), B(5;-2;3), C(3;2;7).
3. А(-2;-1;-2), B(3;0;-2), C(1;4;2). 4. А(-6;0;0), B(-1;1;0), C(-3;5;4).
5. А(-2;-3;-8), B(3;-2;-8), C(1;2;-4). 6. А(1;0;-1), B(6;1;-1), C(4;5;3).
7.
А(-1;4;1), B(4;5;1),
C(2;9;5).![]() 8. А(3;-6;-3), B(8;-5;-3),
C(6;-1;1).
8. А(3;-6;-3), B(8;-5;-3),
C(6;-1;1).
9. А(1;0;0), B(6;1;0), C(4;5;4). 10.А(2;-8;-2),B(7;-7;-2), C(5;-3;2).
11. А(1;-2;3), B(0;-1;2),C(3;-4;5). 12.А(0;-3;6),B(-12;-3;-3),C(-9;-3;-6).
13. А(3;3;-1), B(5;5;-2), C(4;1;1) 14. А(-1;2;-3), B(3;4;-6), C(1;1;-1).
15. А(-4;-2;0), B(-1;-2;4), C(3;-2;1). 16. А(-3;-7;-5), B(0;-1;-2), C(2;3;0).
17. А(3;3;-1), B(1;5;-2), C(4;1;1). 18. А(0;0;4), B(-3;-6;1), C(-5;-10;-1).
19. А(7;0;2), B(7;1;3), C(8;-1;2). 20. А(0;3;-6), B(9;3;6), C(12;3;7).
Задание 5
Даны координаты вершин пирамиды АВСD. Найти:
векторы
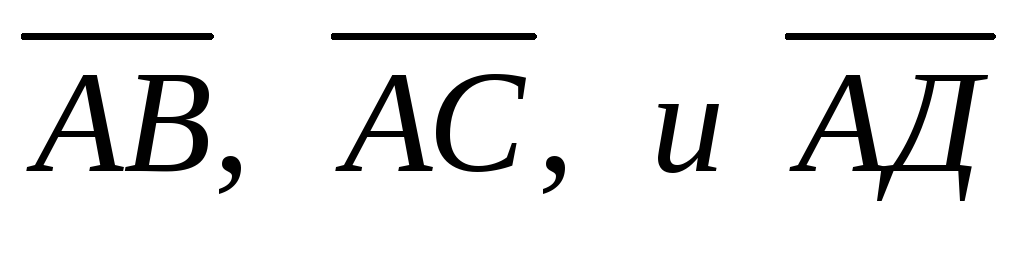 в
системе орт и их модули;
в
системе орт и их модули;угол между векторами
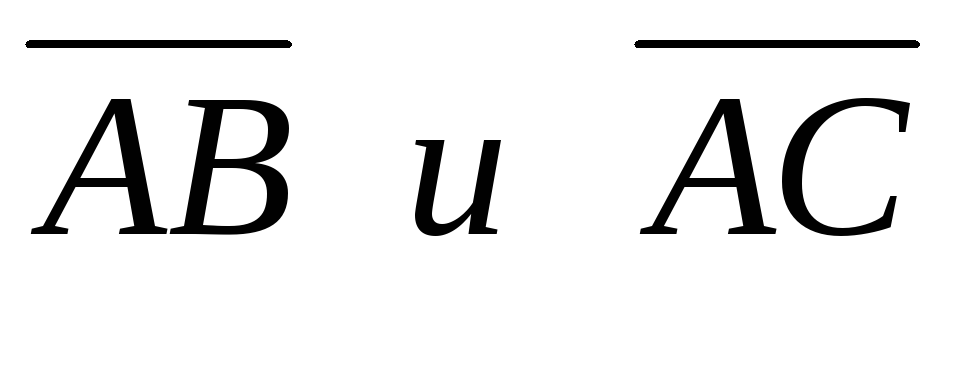 ;
;площадь грани АВС;
объем пирамиды АВСD;
уравнение ребра АВ;
уравнение плоскости АВС;
уравнение и длину высоты, опущенной из точки D на плоскость АВС.
А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
Задание 6
В
задачах 1-20 даны векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Показать, что векторы
.
Показать, что векторы
![]() ,
,
![]() ,
,
![]() образуют базис трехмерного пространства,
и найти координаты вектора
образуют базис трехмерного пространства,
и найти координаты вектора
![]() в этом базисе.
в этом базисе.
1.
![]() (2;1;3),
(2;1;3),
![]() (3;-2;1),
(3;-2;1),
![]() (1;-3;-4),
(1;-3;-4),
![]() (7;0;7).
(7;0;7).
2.
![]() (5;3;1),
(5;3;1),
![]() (-2;-1;2),
(-2;-1;2),
![]() (-2;1;4),
(-2;1;4),
![]() (3;0;1).
(3;0;1).
3.
![]() (1;3;5),
(1;3;5),
![]() (-2;-1;-1),
(-2;-1;-1),
![]() (4;-2;4),
(4;-2;4),
![]() (-7;3;-1).
(-7;3;-1).
4.
![]() (3;1;6),
(3;1;6),
![]() (-2;2;-3),
(-2;2;-3),
![]() (-4;5;-1),
(-4;5;-1),
![]() (3;0;1).
(3;0;1).
5.
![]() (4;1;4),
(4;1;4),
![]() (-2;-1;1),
(-2;-1;1),
![]() (3;1;5),
(3;1;5),
![]() (-3;-2;1).
(-3;-2;1).
6.
![]() (1;2;5),
(1;2;5),
![]() (2;-3;4),
(2;-3;4),
![]() (1;-1;-2),
(1;-1;-2),
![]() (3;0;1).
(3;0;1).
7.
![]() (5;1;2),
(5;1;2),
![]() (3;4;-1),
(3;4;-1),
![]() (-4;2;1),
(-4;2;1),
![]() (-3;5;4).
(-3;5;4).
8.
![]() (2;1;5),
(2;1;5),
![]() (-4;3;5),
(-4;3;5),
![]() (1;-1;-4),
(1;-1;-4),
![]() (4;-1;-3).
(4;-1;-3).
9.
![]() (3;1;4),
(3;1;4),
![]() (-4;2;3),
(-4;2;3),
![]() (2;-1;-2),
(2;-1;-2),
![]() (7;-1;0).
(7;-1;0).
10.
![]() (1;4;2),
(1;4;2),
![]() (5;-2;-3),
(5;-2;-3),
![]() (-2;-1;1),
(-2;-1;1),
![]() (-3;2;4).
(-3;2;4).
11.
![]() (2;1;3),
(2;1;3),
![]() (3;-2;1),
(3;-2;1),
![]() (1;-3;-4),
(1;-3;-4),
![]() (7;0;7).
(7;0;7).
12.
![]() (5;3;1),
(5;3;1),
![]() (-2;-1;2),
(-2;-1;2),
![]() (-2;1;4),
(-2;1;4),
![]() (3;0;1).
(3;0;1).
13.
![]() (1;3;5),
(1;3;5),
![]() (-2;-1;-1),
(-2;-1;-1),
![]() (4;-2;4),
(4;-2;4),
![]() (-7;3;-1).
(-7;3;-1).
14.
![]() (3;1;6),
(3;1;6),
![]() (-2;2;-3),
(-2;2;-3),
![]() (-4;5;-1),
(-4;5;-1),
![]() (3;0;1).
(3;0;1).
15.
![]() (4;1;4),
(4;1;4),
![]() (-2;-1;1),
(-2;-1;1),
![]() (3;1;5),
(3;1;5),
![]() (-3;-2;1).
(-3;-2;1).
16.
![]() (1;2;5),
(1;2;5),
![]() (2;-3;4),
(2;-3;4),
![]() (1;-1;-2),
(1;-1;-2),
![]() (3;0;1).
(3;0;1).
17.
![]() (5;1;2),
(5;1;2),
![]() (3;4;-1),
(3;4;-1),
![]() (-4;2;1),
(-4;2;1),
![]() (-3;5;4).
(-3;5;4).
18.
![]() (2;1;5),
(2;1;5),
![]() (-4;3;5),
(-4;3;5),
![]() (1;-1;-4),
(1;-1;-4),
![]() (4;-1;-3).
(4;-1;-3).
19.
![]() (3;1;4),
(3;1;4),
![]() (-4;2;3),
(-4;2;3),
![]() (2;-1;-2),
(2;-1;-2),
![]() (7;-1;0).
(7;-1;0).
20.
![]() (1;4;2),
(1;4;2),
![]() (5;-2;-3),
(5;-2;-3),
![]() (-2;-1;1),
(-2;-1;1),
![]() (-3;2;4).
(-3;2;4).
