Мерзликин Основы теории ядерных реакторов

По возможностям размещения в заданном объёме активной зоны наибольшего количества топлива (определяемого числом размещаемых в активной зоне ТВС) квадратная решётка уступает треугольной, но является более подходящей для уранграфитового реактора, т.к. графит, уступая воде по замедляющей способности (ξΣs), для обеспечения теплового спектра в реакторе должен использоваться в активной зоне

в большем количестве на единицу массы загружаемого топлива, чем вода.

*) Подсчитано, например, что для получения теплового спектра нейтронов в гомогенной уранграфитовой смеси на каждое ядро урана требуется 80 - 120 ядер углерода, тогда как в уран-водных

гомогенных смесях для этого надо всего 12 - 15 молекул воды. Приблизительно такие же соотношения распространяются и на гетерогенные критические композиции.

В реакторе РБМК-1000 стройная структура квадратной решётки ТВС в активной зоне нарушается из-за необходимости размещения органов управления реактора (подвижных и неподвижных стержней-поглотителей): часть ячеек активной зоны освобождается от ТВС, а их места в пустых технологических каналах замещаются органами СУЗ. Ячейки, занятые органами СУЗ, в активной зоне реактора образуют свою квадратную решётку, повернутую относительно квадратной решётки ТВС на угол в 45о (рис.4.4). Таким образом, получается, что действительно повторяющимся компонен-

том структуры активной зоны РБМК является не одна ячейка, а шестнадцать их, ко-

торые образуют полиячейку активной зоны.

Таблица 4.1. Некоторые характеристики гетерогенных структур реакторов типа ВВЭР и РБМК.

Итак, мы познакомились с основными характеристиками, определяющими гетерогенную структуру активных зон тепловых реакторов отечественных АЭС. Разумеется, сказанное не может претендовать на полноту описания конструкции активных зон; с детальным изучением конструкции реакторов ещё предстоит иметь дело по окончании изучения теории реакторов; сейчас же, наоборот, важно получить самые общие представления об устройстве активных зон реакторов ради понимания теоретических построений, касающихся гетерогенности структур реакторов.

Тема 5

ЗАМЕДЛЕНИЕ НЕЙТРОНОВ В РЕАКТОРЕ И ЕГО РАЗМНОЖАЮЩИЕ СВОЙСТВА

5.1. Общие начальные рассуждения

При рассмотрении нейтронного цикла теплового реактора в п.3 была получена зависимость эффективного коэффициента размножения от характеристик отдельных сторон нейтронного цикла:

kэ = η ε ϕ θ pзpт.

Из шести сомножителей правой части этой формулы величиной, непосредственно связанной с процессом замедления нейтронов в реакторе, является величина pз - вероятности избежания утечки замедляющихся нейтронов.

Вероятность избежания утечки замедляющихся нейтронов - это доля нейтронов, избежавших утечки из активной зоны при замедлении, от всех нейтронов поколения, начавших процесс замедления в активной зоне.

Первый вопрос, естественно возникающий в начале изучения новой для нас величины: какие факторы определяют эту величину?

Обращаясь к житейскому опыту, можно предположить что величина pз явно должна зависеть от:

-геометрии активной зоны (то есть от её формы и размеров);

-каких-то физических свойств композиции материалов активной зоны реактора.

Первое предположение не только интуитивно, оно имеет и некоторое логическое обоснование, которое выглядит приблизительно так.

Быстрые нейтроны деления рождаются во всём объёме активной зоны, а утечку за пределы активной зоны могут испытывать лишь нейтроны, замедляющиеся в пределах ограниченного слоя вблизи границ активной зоны. Следовательно, чем больше размеры активной зоны, тем меньшую часть общего объёма активной зоны будет составлять та его периферийная часть, из которой происходит утечка замедляющихся нейтронов, и тем выше должна быть величина вероятности избежания утечки замедляющихся нейтронов.

Понятно, что с возрастанием размеров активной зоны до очень больших величин доля утекающих из неё замедляющихся нейтронов устремляется к малым величинам (в пределе - к нулю при бесконечном возрастании размеров). Значит, величина вероятности избежания утечки замедляющихся нейтронов из активной зоны бесконечных размеров равна единице.

Подобное рассуждение вполне уместно для активной зоны любой геометрической формы: как для самой простой сферической, так и для наиболее распространённой в энергетических реакторах активной зоны цилиндрической формы. Логический результат будет принципиально тот же, за исключением разве что одного: распределение вероятности избежания утечки замедляющихся нейтронов по поверхности цилиндрической активной зоны (в отличие от сферической) существенно неравномерно. Например, в углах продольного сечения цилиндрической активной зоны нейтронам представлены большие возможности для утечки из активной зоны, чем посреди боковой цилиндрической поверхности, а на цилиндрической части поверхности - большие возможности, чем в центральной части плоских ее торцов.

А раз распределение вероятности по поверхности активных зон зависит от их формы, значит, и сама величина вероятности pз зависит от формы активной зоны.

Приведенные простые рассуждения ценны ещё одним: они вплотную подводят к мысли о том, что pз определяется не только геометрией активной зоны, но и какими-то физическими свойствами среды активной зоны. Поскольку толщина слоя любой заданной формы, из которого происходит утечка замедляющихся нейтронов, может определяться только природными свойствами среды этого слоя.

Для нормального человека это очевидно, хотя и порождает неизбежный уточняющий вопрос: какие именно физические свойства материальной среды активной зоны имеются в виду?

Ведь у каждого конкретного вещества физических свойств много: теплоёмкость, плотность, теплопроводность, вязкость, магнитная проницаемость, поглощающая способность, рассеивающая способность... Всё это разные физические свойства, характеризующие каждое конкретное вещество с различных физических точек зрения, и каждое из этих свойств имеет свою количественную меру.

Очевидно, речь должна идти о каких-то замедляющих свойствах среды активной зоны, характеризующих её свойство в той или иной степени быстро замедлять нейтроны. Чем быстрее замедляющийся нейтрон превращается в тепловой, тем меньшее смещение в пространстве среды он испытывает, и тем меньше у него возможностей оказаться за пределами активной зоны во время замедления. Иными словами, как показывают приведенные рассуждения, из всех замедляющих свойств среды важнейшую роль должна играть её способность давать определенное среднее смещение нейтрона в ней в течение процесса замедления.

Средняя длина замедления среды (lз) - это осреднённая для всех замедляющихся нейтронов величина пространственного смещения их за время замедления (т.е. от точки рождения быстрого нейтрона до точки, где он замедляется до теплового уровня).

Следует подчеркнуть, что lз - характеристика не нейтронов, а среды, вещества, так как с позиций грамматики термин "средняя длина замедления нейтронов в среде" звучит немного обманчиво. (Обычно, когда мы говорим, например: "средняя скорость самолета Ту-154 равна 960 км/час", - нам ясно, что характеристика "скорость" относится к однозначно определённому объекту - самолету Ту-154. В данном же случае, когда мы слышим: "средняя длина замедления нейтронов", - по аналогии чисто грамматического свойства может показаться, что речь идёт о характеристике нейтронов, тогда как это - характеристика среды, отражающая её способность давать строго определённое среднее пространственное смещение нейтронов в процессе их замедления.).

Итак, pз = f (геометрии а.з.; замедляющих свойств среды а.з.).

Но так как любое из физических свойств должно иметь свою количественную меру, то эту логическую зависимость можно переписать так:

рз = ¦(какого-то геометрического параметра а.з.; какой-то характеристики замед-

5.2. Характеристики замедляющих свойств веществ

Средняя длина замедления - сложная характеристика, представляющая собой комбинацию более простых характеристик замедляющих свойств веществ.

Познакомимся с самыми основными из них, нужными нам для дела.

5.2.1. Макросечение рассеяния вещества. Для того, чтобы реактор был тепло-

вым, то есть большинство делений в нём происходило под действием тепловых нейтронов, последние надо непрерывно получать, необходимо наладить процесс непрерывного замедления быстрых нейтронов, рождаемых в делениях ядер топлива. По-

скольку топливо обладает слабыми замедляющими свойствами, единственным средством получения в реакторе нейтронов теплового спектра является введение в состав активной зоны специальных веществ – замедлителей. Причём, в количестве, достаточном для того, чтобы интенсивность трансформации быстрых нейтронов деления в тепловые в активной зоне была существенно (во много раз) большей, чем интенсивность поглощения нейтронов в процессе их замедления.

Замедляющие свойства вещества должны определяться, очевидно, величиной скорости уменьшения кинетической энергии нейтронов в единичном объёме вещества в единицу времени. Это уменьшение кинетической энергии нейтронов происходит в реакциях рассеяния на ядрах среды. Чем больше реакций рассеяния происходит в 1 см3 среды за 1 с, тем больше энергии отнимает этот единичный объём вещества за 1 с у замедляющихся в нём нейтронов, и тем, следовательно, лучшим замедлителем может служить это вещество.

Но число рассеяний в 1 см3 вещества за 1 с - это не что иное, как скорость реакции рассеяния на ядрах этого вещества:

Rsi = Σsi Ф,

следовательно, вещество будет тем лучшим замедлителем, чем выше величина его макросечения рассеяния Σs.

И можно было бы считать Σs определяющей характеристикой замедляющих свойств веществ, если бы ядра всех веществ в одиночных рассеяниях отнимали у любого одиночного нейтрона одинаковую порцию энергии. Но в действительности дело обстоит не так: во-первых, ядра различных атомов отнимают у замедляющихся нейтронов существенно различные количества кинетической энергии, а, во-вторых, даже у одного определённого сорта ядер величина этой порции сильно зависит от величины энергии рассеиваемого нейтрона. То есть величина потерь энергии нейтроном в последовательных рассеяниях в процессе замедления от рассеяния к рассеянию падает даже при замедлении на ядрах одного сорта.

Поэтому явно нужна ещё какая-то характеристика замедляющих свойств для каждого сорта ядер, которая бы отражала способность этих ядер отнимать у нейтрона в одиночном рассеянии определённую среднюю кинетическую энергию.

5.2.2. Среднелогарифмический декремент энергии. Э.Ферми при разработке модели непрерывного замедления первым предположил, что закономерность уменьшения нейтроном энергии в последовательных рассеяниях на ядрах однородной среды имеет экспоненциальный характер, то есть, начиная замедление с начального уровня энергии Ео, после k последовательных рассеяний нейтрон снижает свою кинетическую энергию до уровня:

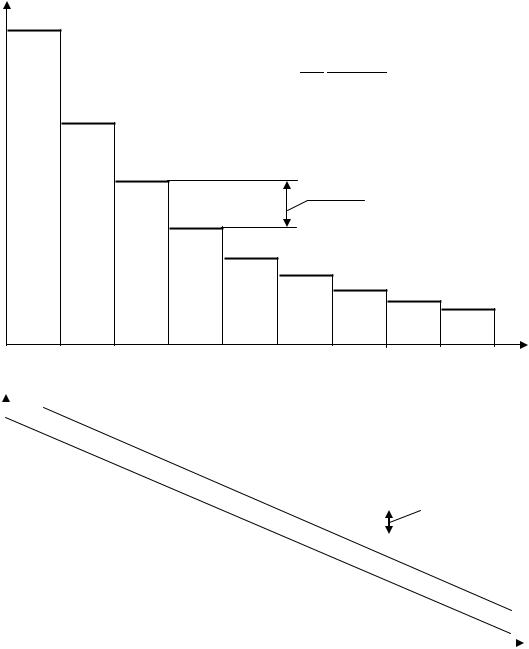
В обычной системе координат (Е - k) дискретный процесс уменьшения нейтроном энергии имеет вид лесенки с разновысокими ступенями; в полулогарифмической системе координат (lnE - k) тот же процесс замедления трансформируется в лестницу со ступенями равной высоты (рис.5.1)

Таким образом, единственной неизменной величиной в процессе экспоненциального замедления нейтрона является уменьшение натурального логарифма энергии нейтрона в одиночном рассеянии.

Уменьшение натурального логарифма энергии замедляющегося нейтрона в одиночном рассеянии, усреднённое по всем рассеяниям на ядрах однородной среды, называется среднелогарифмическим декрементом энергии этих ядер (или этой среды, если речь о более общем случае сложной среды, состоящей из нескольких сортов ядер).

В реальных однородных веществах, где процессы рассеяния замедляющихся нейтронов подвержены многим случайностям, величина ξ может для отдельных рассеяний

при разных энергиях нейтронов отклоняться в ту или иную сторону от некоторого среднего своего значения. Поэтому для получения действительной характеристики замедляющих свойств ядер и производится операция усреднения.

E

Е0

Общая закономерность: Еk = E0 exp (- ξ k)

0 1 2 3 4 5 6 7 Номер рассеяния k

Рис.5.1 .Характер уменьшения кинетической энергии нейтрона при замедлении, иллюстрируемый

в натуральных и полулогарифмических координатах.

Величина среднелогарифмического декремента энергии для ядер различной массы легко вычисляется по формулам нейтронной физики:

где A, а.е.м. - массовое число ядра-рассеивателя.

*) Для водорода (А = 1) величина ξ принимается равной 1.

С дальнейшим ростом A величина среднелогарифмического декремента энергии ядер быстро уменьшается и уже при A > 3 для вычисления её можно с достаточной точ-

ностью пользоваться упрощённой формулой:

Для ядер тяжёлых замедлителей (с A >10) формула ещё проще:

Возвращаясь к начальным рассуждениям, мы должны констатировать: лёгкие яд-

ра - лучшие замедлители нейтронов, чем более тяжёлые: чем больше A, тем меньше величина ξ, и тем меньше не только уменьшение логарифма энергии нейтрона в одном рассеянии, но и абсолютная средняя потеря энергии в этом рассеянии, которая связана с ξ простой зависимостью:

рифмический декремент энергии вещества ξ, взятые порознь, являются однобокими характеристиками замедляющих свойств: одна из них учитывает только интенсивность рассеяний в единичном объёме вещества, другая - только энергетическую сторону процесса замедления на ядрах вещества.

А вот произведение этих двух величин как раз и даёт ответ на вопрос, какой замедлитель является лучшим. Действительно, лучшими замедляющими свойствами обладает то вещество, которое имеет более высокие значения ξ и Σs, а, значит, обладает более высоким значением произведения ξΣs.

Произведение ξΣs называется замедляющей способностью вещества.

По величине замедляющей способности можно сравнивать замедляющие свойства различных замедлителей, составлять суждение, какой из замедлителей является лучшим, и подбирать материалы-замедлители для активных зон тепловых реакторов.

5.2.4. Коэффициент замедления вещества. Если замедляющая способность ве-

щества ξΣs является исчерпывающей характеристикой природной склонности вещества к отбору энергии у замедляющихся в нём нейтронов, то это ещё не означает, что большая её величина даёт пропуск этому веществу для использования в качестве замедлителя в тепловом реакторе.

Важно, чтобы замедлитель не только интенсивно замедлял нейтроны, но и не поглощал их в процессе замедления: не будем забывать, что любой нуклид обладает ненулевым микросечением радиозахвата в диапазоне энергий замедления нейтронов в реакторе. Поэтому при равных величинах замедляющей способности материалов с точки зрения сохранения замедляющихся нейтронов лучшим замедлителем будет тот из них, у которого меньше величина макросечения поглощения эпитепловых нейтронов.

Количественной мерой этой комплексной способности вещества хорошо замедлять и одновременно хорошо сохранять замедляющиеся нейтроны служит величина коэффициента замедления.

Коэффициент замедления вещества - это величина отношения замедляющей способности вещества к его поглощающей способности в интервале энергий замедления (измеряемой величиной среднего значения макросечения поглощения вещества в этом интервале).

5.2.5. Число рассеяний, потребное для замедления нейтронов до теплового уровня. Если средняя энергия, с которой нейтроны деления начинают процесс замедления, равна Ео (равная 2 МэВ), а конечная энергия интервала замедления (энергия сшивки) равна Ес, то эти значения энергий можно отметить точками на шкале логарифма энергии нейтронов:

А так как среднелогарифмическая потеря энергии нейтрона в одиночном рассеянии равна ξ, то является очевидным, что для замедления нейтрона от Ео до Ес необходимо, чтобы нейтрон испытал за весь процесс замедления

рассеивающих соударений с ядрами замедляющей среды. Это число рассеяний, потребное для полного замедления нейтрона деления до теплового уровня, также может служить характеристикой замедляющих свойств среды, составляющей активную зону теплового реактора.

5.2.6. Сравнение характеристик лучших природных замедлителей. Цифровые данные для сравнительной оценки замедляющих свойств шестёрки лучших природных замедлителей приведены в табл.5.1.

Таблица 5.1. Характеристики шести лучших природных замедлителей.

Таким образом, лёгкая вода (H2O) является первым замедлителем по величине замедляющей способности, но по величине коэффициента замедления она на пятом месте, уступая тяжёлой воде, бериллию, оксиду бериллия и графиту потому, что вода обладает более высоким значением макросечения поглощения замедляющихся нейтронов.

Тяжёлая вода, обладая самым высоким значением коэффициента замедления, является почти идеальным замедлителем для тепловых реакторов. Но целый букет негативных качеств: радиоактивность, редкая распространённость в природе, энергоёмкая и дорогостоящая технология получения чистой тяжёлой воды (0.5% примесей в тяжёлой воде снижают коэффициент замедления её почти на порядок!), дополнительные трудности с обеспечением особого водного режима первого контура, порождают добавочные проблемы как для конструкторов, так и для эксплуатационников.

Бериллий и оксид бериллия не получили широкого распространения в качестве замедлителя для энергетических реакторов из-за высокой токсичности бериллия и его соединений (усложняющей как технологию получения высокочистого бериллия, так и технологию изготовления деталей внутриреакторных конструкций), высокой стоимости бериллия и малой его радиационной стойкости в условиях мощного нейтронного и гамма-облучения в активной зоне энергетического реактора.

Отсутствие у графита недостатков, свойственных бериллию и его оксиду, и сделало его основным замедлителем в уран-графитовых реакторах отечественных АЭС.

5.3. Возраст нейтронов в среде

Познакомимся с ещё одной комплексной характеристикой замедляющих свойств различных сред, называемой возрастом нейтронов, поскольку именно она является ключевым понятием теории замедления и чаще иных характеристик встречается в формулах и уравнениях теории реакторов.

Путь к пониманию этой характеристики проходит через понятия анизотропии рассеяния и транспортного макросечения вещества.

5.3.1. Анизотропия рассеяния и её мера. Ранее (п.2.4.1) мы уже познакомились с понятием средней длины свободного пробега рассеяния нейтронов:

величиной, обратной макросечению рассеяния среды. Эта величина в нашем понимании ассоциируется со средним расстоянием по прямой, проходимым нейтроном между двумя последовательными рассеяниями.

Казалось бы все просто: независимо от того, движутся или покоятся 1-ое и 2-ое ядра (рис.5.2), пробег нейтрона между двумя последовательными рассеяниями определяется положением в пространстве этих двух ядер в моменты их столкновения с нейтроном. На деле пробег между двумя рассеяниями - вещь более сложная даже в том простейшем случае, если предположить, что оба ядра в моменты столкновения покоятся. Такая схема была бы справедливой, если бы акт рассеяния был актом простого механического соударения нейтрона с ядром.

ψ - угол рассеяния

Ядро, на котором рассеивается нейтрон Следующее ядро, на котором

происходит рассеяние нейтрона Длина пробега рассеяния λs

Рис.5.2. Схематическое изображение двух последовательных рассеяний нейтрона и средняя длина свободного пробега рассеяния в образно-механическом представлении.

Но (вспомнить п.2.1.2) акт одиночного рассеяния является полноправной нейтронной реакцией, начинающейся с проникновения нейтрона в ядро, образования возбуждённого составного ядра, и заканчивающейся испусканием нейтрона возбуждённым ядром. Поэтому, ставя вопрос о пробеге нейтрона между последовательными рассеяниями, уместно вначале задать вопрос: сколько времени нейтрон будет находиться в составе возбуждённого ядра, и куда будет двигаться это возбуждённое ядро в течение этого времени?

Если одиночное рассеяние нейтрона в любом направлении равновероятно, то, очевидно, что после большого множества рассеяний нейтрон окажется вообще неспособным на какое-то заметное смещение в пространстве. Ведь если каждому направлению испускания нейтрона после рассеяния на одном ядре соответствует с той же вероятностью противоположное направление испускания в одном из последующих рассеяний на иных ядрах, то это значит, что мечущийся во всех мыслимых направлениях нейтрон "скачет" около одной фиксированной точки пространства среды, не сдвигаясь относительно этой точки, подобно неопытному туристу в лесу, ежеминутно меняющего направления, но не могущего удалиться от той точки леса, где он впервые обнаружил, что заблудился.

А если же нейтрон имеет какое-то закономерно-предпочтительное направление после рассеяния, то в процессе последовательных рассеяний на ядрах среды он будет

постепенно удаляться от точки первого рассеяния в этом предпочтительном направлении.

Понятно, что на вопрос о равноили неравновероятности рассеяния нейтрона по различным направлениям дать точный доказательный ответ мы не в состоянии: одиночные нейтроны пока не наблюдались даже с помощью самого современного электронного микроскопа. Поэтому судить о вероятностях рассеяния нейтрона в разных направлениях можно только на основе косвенных признаков, фиксируемых в тонких физических экспериментах.

Пространственное смещение нейтронов в процессе их рассеяния установлено как непреложный факт, и это потребовало теоретических объяснений. Поскольку принципиальных или логических противопоказаний к любому направлению рассеяния нейтрона ядром нет, условились считать, что покоящиеся ядра испускают рассеянные нейтроны равновероятно по всем возможным направлениям (в пределах 4p стерадиан телесного угла). Коротко такое рассеяние называют изотропным.

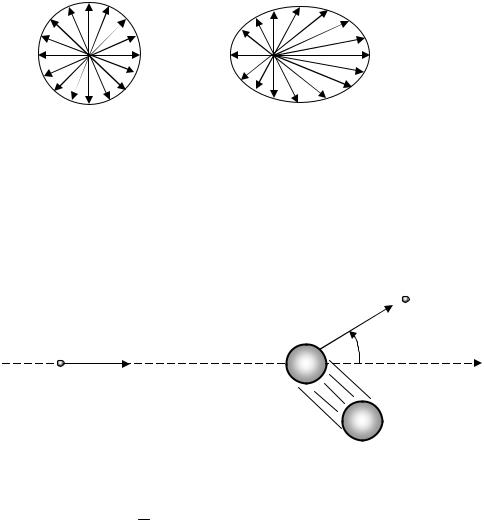
Если величину вероятности рассеяния нейтрона в определённом направлении изображать в виде вектора, то изотропное рассеяние на плоской векторной диаграмме будет выглядеть, как показано на рис.5.3а: векторы вероятности по всем направлениям имеют равную длину, а огибающая линия концов этих векторов - окружность. Нетрудно представить себе подобную теоретическую схему изотропного рассеяния и в трёхмерном пространстве - в виде этакого "ежа" с равномерно расположенными колючками равной длины

Изотропное Анизотропное

Рис.5.3. Упрощенные (плоские) схемы изтропного и анизотропного рассеяния.

Всякое другое рассеяние, то есть такое, при котором определённые направления испускания рассеянных ядрами нейтронов оказываются более вероятными, чем другие,

называется анизотропным.

В качестве направления начала отсчёта углов рассеяния обычно выбирается направление движения нейтрона до рассеяния.

Углом рассеяния (ψ) в системе координат, жёстко связанной с реактором, называют угол между направлениями движения нейтрона после и до рас-

сеяния (рис.5.4).

Рис.5.4. Иллюстрация к понятию плоского угла рассеяния.

Мерой анизотропии рассеяния служит средний косинус угла рассеяния: